Eight classification algorithms were applied to 1,123 time series prediction tasks, in order to rank the algorithms according to accuracy and generality, and to replicate previous experiments addressing the possible existence of so-called "silver bullet" algorithms which produce nearly maximal performance on nearly all real-world problems without requiring customization.  The algorithms under consideration were neural networks, autoregressive moving averages, genetic programming, polynomial regression, radial basis functions, binary decision trees, hidden Markov models, and k-nearest-neighbors with feature selection.  These algorithms were presented with short regions of a time series and were expected to predict the discretized value of the series at several lead times into the future.  The most consistently accurate algorithm was found to be polynomial regression, followed closely by radial basis functions and genetic programming.  However, none of these algorithms were found individually to qualify as a "silver bullet" for time series prediction.  Suggestions are made regarding the construction of a toolbox of algorithms sufficient in coverage to achieve nearly maximal performance on novel problems with high confidence.
 

Introduction

Investigation of the capabilities of prediction techniques can improve not only our ability to manipulate systems for personal gain, but also our understanding of the basic mechanisms involved in the process of coadaptation between biological organisms, especially in the case of animal learning.

Although animal brains are often conceptualized as being roughly analogous to neural networks, the actual algorithmic processes which emerge from the large-scale  operation of a brain may be more appropriately modeled by something other than a backpropagation neural network.  For this reason, it is not unreasonable to consider non-connectionist models in the study of prediction facilities in animals.

However, the present study is merely concerned with investigating the relative capabilities of several popular prediction algorithms.  In particular, results are presented from an empirical study in univariate, categorical time series prediction which utilized a large number of time series collected from real physical, biological, and economic systems.

The prediction problems were categorical in the sense that the task is not to predict the exact value of a real variable, but to predict which of a finite number of non-overlapping ranges the variable falls into.  This not only simplifies the comparison and renders a larger number of algorithms potentially applicable, but it also reflects the fact that many practical prediction tasks are actually of a categorical variety; it is often of great value to know whether a variable will rise or fall by a certain amount within a given time interval.

The actual lead times used in the prediction were 1, 5, and 10 time units into the future.  These were chosen to represent short- and long-term prediction tasks, although it is recognized that for some applications, 10 time units would not be considered long.

The algorithms under consideration were neural networks, autoregressive moving averages (ARMA), genetic programming, polynomial regression, radial basis functions, binary decision trees, hidden Markov models (HMM's), and k-nearest-neighbors with feature selection.

These eight algorithms were all applied to the same set of problems, and their classification accuracy was assessed and compared to determine not only which algorithm performed most competitively, but also how often an algorithm can be expected to produce maximal accuracy on novel problems.
 

Methods

DATA COLLECTION

Time series were collected from various sites on the internet (see references), and a significant number were also taken from a disk accompanying [Masters 1995].  Series of the same length were compared numerically to eliminate duplicates, resulting in 381 distinct series.
 

PREPROCESSING

A low-pass filter was applied to each time series to produce additional inputs for the prediction algorithms.  The filters were computed by applying a Gaussian envelope (=0.03) to the series in the frequency domain.  Fourier transforms were computed using subroutines from [Masters 1995].  The filter did not utilize future information -- filtering was performed anew at each time point, using only data points from the past.  The cut-off frequency was chosen (for differenced series) by computing the power spectrum and finding that frequency f having half the power both above and below f.  For nondifferenced series, the frequency was chosen to be 0.1.  To give the filtering sufficient data, training/test case windows did not start until point 20 in the series.  All other filtering details followed [Masters 1995].

If the series consisted only of positive numbers, it was log-transformed; otherwise, it was -transformed.

Differencing was performed to remove stationarity.  In addition, seasonal differencing was performed if the description of the series contained the word monthly and both a positive auto-correlation at lag 12 of at least 0.25 and a negative autocorrelation at lag 6 at least as extreme as -0.25 were detected.
 
 

PREDICTION TASKS

Each time series was used to construct three prediction tasks, for a total of 1,143 problems.  However, due to the occurrence of missing values and various other difficulties, only 1,123 problems were used in the analysis.

In each of the three prediction tasks, a seven-point sliding window was moved across the time series (in an overlapping fashion) to produce a set of test cases.  Note that because the series was differenced before extracting these windows, a sequence of seven differences actually corresponds to eight data points in the original series.

For each test case, a prediction algorithm was expected to predict the value at some number of points into the future.  The three tasks differed in the lead time for the prediction, as well as in the inputs provided to the algorithm and the form of discretization applied to the predicted value to facilitate scoring.

The details are as follows:

Task 1 = Predict change over one time unit.

Predict one of 10 categories denoting the change from the last window value to the first value following the window.

Inputs :

7 previous differences

1 most recent low-pass point (not difference)

7 previous low-pass differences

Note that low-pass point refers to the output of a low-pass filter applied to the original series, not the differenced, compressed series.

Because this is a short-term prediction task, only one low-pass point was provided, in order to establish the level of the original (non-differenced) series.  The low-pass differences were supplied for the purpose of augmenting the information in the raw differences by providing a smoother view of the recent behavior of the series.  The unfiltered differences provided information about high-frequency movement, which would presumably be useful for short-term prediction.

Predict that the signal will rise by at least , fall by at least , or neither, between the end of the window and the 5^th point past the end of the window.

Inputs:

7 previous differences

7 previous low-pass points (not differences)

1 most recent low-pass difference

Note that low-pass difference refers to the output of a low-pass filter applied to the differenced, compressed (log- or -transformed) series.

Because this is a relatively long-term prediction task, the low-pass points were supplied in order to provide information about low-frequency movement.  The single low-pass difference helps establish the recent level of the (smoothed) differenced series.  Previous differences were provided simply for completeness.

Task 3 = Predict change over 10 time units.

Predict that the signal will rise by at least , fall by at least , or neither, between the end of the window and the 10^th point past the end of the window.

Inputs:

7 previous differences

7 previous low-pass points (not differences)

1 most recent low-pass difference

These are the same inputs as provided in task 2, and carry the same justification.

For Task 1, the ten categories were chosen to be of uniform size; i.e., range/10.  It may be observed that this provided a very small amount of future information to the prediction algorithms by establishing that at least one future value will fall into the highest (conversely, the lowest) category, but this should be largely irrelevant for the purpose of comparison.

For Tasks 2 and 3, the three category domains were separated by multiplying 0.43 times the standard deviation (), because the distributions for a sample of problems all appeared to be mound-shaped, and for a standard normal distribution, Z=0.43 divides the distribution into three parts of equal area (33.33%).  Thus,

These category thresholds were provided to those algorithms which predicted real values rather than categories, so that their predictions could be discretized, for the purpose of evaluation.  Although this practice may seem somewhat artificial, it greatly simplifies the comparison of categorical and real-valued prediction algorithms.

Each test case consisted of the 15 task-specific inputs described above and a single task-specific output (expected prediction), for a total of 16 values.  Test cases were sorted according to their associated times in the original time series and then split evenly into two sets, corresponding to cases from the first half of the series and those from the second half.  These were then used as training sets and test sets, respectively, for the learning algorithms.  Thus, the algorithms were trained on the first half of the time series and tested on the second half.
 
 

ALGORITHMS

Eight prediction algorithms were compared by applying each algorithm to all of the test problems and evaluating prediction accuracy, as described in the next section.  The computing environment in which these algorithms were exercised is described in [Majoros 2000b].

The algorithms tested were as follows:

• Backpropagation neural networks (NET)
• Entropy-based binary decision trees (TRE)
• K-nearest-neighbors with feature selection (FS)
• Genetic programming (GP)
• Autoregressive moving averages (ARMA)
• Hidden Markov models (HMM)
• Polynomial regression (POLY)
• Radial basis functions (RAD)

• Simple linear regression (LIN)
• Majority rule (MAJ)
• Same-value rule (SAM)
• Random guessing (RND)

The first baseline (LIN) was simple linear regression on the actual data points.  Least-squares regression was used to fit a straight line to each window of 8 points (i.e., corresponding to 7 differences).  The slope of this line was used to predict the value one time unit beyond the end of the window.  This value was then discretized according to the dictates of the task at hand (i.e., ten categories for Task 1, five categories for Tasks 2 and 3), using the actual category boundaries, as described in the previous section.

The SAM baseline employed a "same change" strategy -- it predicted that the first difference past the end of the window would be of the same magnitude and direction as the last difference in the window.  Thus, the category predicted by SAM is the same as the actual category of the previous test case.

The third baseline, RND, was the uniform random guess -- guessing each category with equal probaability.  The accuracies reported for this baseline are expected values, given the distribution of categories observed in the test set.  Expected accuracy is computed from total error, as described in the next section.  Expected total error is given by

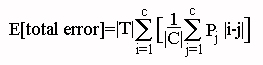
for T the set of test cases and C the set of categories.  The inner sum is the expected magnitude of error when RND guesses category i.  We then sum this over all i, assuming a uniform probability of 1/|C| of selecting each i.

The last baseline (MAJ) was the majority rule -- observing which category occurred most often in the training set and then predicting that category on every case in the test set.

The actual prediction algorithms were as follows.  Each of these algorithms was executed by unpublished software written by the author, except as noted.

Neural Networks:  The backpropagation neural networks that were used are described in [Majoros 2000a], with the following differences.  Each network had only one hidden layer with either 4 or 6 hidden nodes and underwent either 80 or 200 iterations of backpropagation, giving rise to a total of 4 possible parameterizations.  Each parameterization was replicated 24 times for a total of 96 runs on each problem, with the highest-scoring replicate used for the purpose of evaluation.  Learning rate was set at 0.21.  This took approximately 5 days of processing.

Genetic Programming:  The genetic programming methodology followed [Majoros 2000a], except as noted here.  A single run consisted of a population of 200 individuals evolving for 200 generations.  Forty runs were executed per problem, with the best run providing the score on that problem.  This took approximately 4.5 days of processing.

K-Nearest-Neighbors with Feature Selection:  This method is conceptually very similar to "Lorenz' method of analogues" [Kantz and Schreiber 1997, p45].  Feature selection, which was performed by dropping features with low F-ratio, can be roughly equated to adaptively picking the embedding dimension in the Lorenz method.  Details are given in [Majoros 2000a].

Decision Trees:  Full binary decision trees were built as described in [Majoros 2000a] from the training sets and then pruned according to all possible entropy cutoff values.  Every pruned tree was tested on the test set, and the best score was taken as the score on that problem.

Autoregressive Moving Average:  Timothy Masters' NPREDICT program [Masters 1995] was used to train and exercise an ARMA(4,1) model.  The predictions were discretized as described in the previous section.

Hidden Markov Models:  Values in the differenced series were discretized into n{5,8} intervals and then used to train a set of m-state hidden Markov models (HMM's), 4m8, with random topologies (0.75 transition density) using the Baum-Welch (Forward-Backward) algorithm for up to 400 iterations, or until the log likelihood changed by less than 0.001.  A separate HMM was trained on each category C to estimate the likelihood P[T|C] for test case T and category C.  Categories were then predicted on the test set using maximum likelihood.  The actual training algorithm followed [Durbin 1999], but with necessary corrections.

Polynomial Regression:  Least-squares regression was used to fit an n^th-degree polynomial (1n7) to a sequence of m contiguous values from the original untransformed series in order to predict the next value, which was then discretized as usual.  For Task 1, values of m{3,4,5} were investigated, for Task 2 m{10,20,30,40}, and for Task 3 m{20,30,40}.  However, for the shorter time series the larger window lengths were used only if they did not result in fewer than 30 test points on which to evaluate accuracy.

Radial Basis Functions:  Least-squares regression was used to fit a model of the form

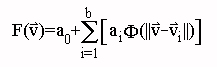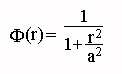, [Kantz and Schreiber 1997]

were obtained by attractor reconstruction (i.e., by taking subsequences of a fixed window length).  In addition to parameter a{10,100,1000,10000}, this method was parameterized by the number of basis vectors b{4,5,6,7,8,10,12,14,18,22} and the attractor dimension d{4,5,6,7,8,10,12,14,18,22}, with the constraint that bd.

ACCURACY ASSESSMENT

The accuracy of an algorithm on a particular problem was scored by computing

for category set C and test set T.  For Task 1, C={x|1x10}, and for Tasks 2 and 3, C={1,2,3}.  Total prediction error, E

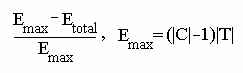
Mean accuracy scores and mean ranks of scores were compared between algorithms by two separate analyses of variance (ANOVA), followed by multiple comparisons using the Tukey test.  All significance levels were set to the 0.05 level.  In addition, ANOVA was applied to accuracy scores on Tasks 1, 2, and 3, separately.

These analyses were performed using unpublished software written by the author.  Statistical procedures and critical values were taken from [Zar 1996].
 

FRACTAL DIMENSION

Three measures of fractal dimension (correlation dimension, information dimension, and capacity dimension) were computed using the program fd3, written by John Sarraille and Peter DiFalco, which is based on [Liebovitch and Toth 1989].  However, this program could be applied only to series of sufficient length.  Series which were too short (a small minority) were excluded from this part of the analysis.

Linear correlation coefficients were computed between accuracy scores and all three measures of fractal dimension in order to test for a (linear) relationship between fractal dimension and predictability.
 

LYAPUNOV EXPONENTS

Maximum Lyapunov exponents were estimated using the programs BASGEN and FET written by Alan Wolf [Wolf 1985].  Documentation accompanying these programs provides guidance for choosing appropriate parameter values.  Of these, the most laborious to obtain was the mean orbital period for the underlying attractor.  This parameter was estimated for each time series as follows.

Embedding dimensions between 4 and 20 were considered.  For each dimension in that range, mean orbital period was estimated.  Each such estimate also provided a "power" measure (described below).  The mean orbital period with the highest power was selected, and then the lowest embedding dimension (also a parameter to Wolf's programs) which gave rise to that orbital dimension was taken to be the embedding dimension for the series.

To estimate the mean orbital period at a given dimension, attractor reconstruction was performed at that dimension.  Then for each point in the attractor, the distances to all temporally preceding points were computed.  These "neighbors" were sorted by distance, and a search was made for the neighbor which was closest geometrically without being too close temporally.  A neighbor was considered too close temporally if all other neighbors which were even closer temporally than this neighbor were also closer geometrically.  The temporal distance to this neighbor was taken as one estimate of orbital period.  Observing the distribution of these estimates over all the points in the attractor, one can then identify peaks in the distribution.  In particular, the leftmost such peak having a height at least half that of the highest peak was taken as the location of the mean orbital period for this dimension.  The "power" of the corresponding frequency was then estimated by summing the heights at all multiples (i.e., harmonics) of this period in the histogram.

This method was found to perform well in preliminary tests, where it was observed that the estimates of orbital period often tended to stabilize with increasing dimension, or at least to remain close to multiples ("harmonics") of the chosen period.

Linear correlation coefficients were computed between maximum Lyapunov exponents and the scores of each algorithm on Task 1, Task 2, and Task 3 problems separately, since Lyapunov exponents measure divergence on the attractor over time, and therefore might be expected to reflect difficulty in long-term prediction.  Correlation coefficients were also computed between accuracy and mean orbital period, and also between accuracy and embedding dimension, as estimated above.
 

HURST EXPONENTS

Hurst exponents were estimated using a very crude procedure roughly following [Peters 1996].  The procedure is based on rescaled range analysis.  Rescaled range (range/) was plotted for progressively longer initial subsequences on a log-log graph and least-squares regression was used to fit a straight line to an initial portion of the plot.  In order to choose the end point for the regression, pairs of straight-line regressions were repeatedly performed on all initial and terminal portions of the plot delimited by each point on the interior 1/3rd of the plot, and the pair minimizing the summed coefficients of determination was selected.  The slope of the first (leftmost) of these selected regression lines was taken to be a very rough estimate for the Hurst exponent.

Linear correlation coefficients were computed between scores and Hurst exponents separately for the three tasks.
 
 

ADDITIONAL ANALYSES

Linear correlation coefficients were also computed for the following:

• Task n accuracy (1n3) versus autocorrelation at lag L (1L17), and also Task n accuracy versus the absolute value of autocorrelation at lag L, for both the original series and the differenced series.  Note that this entails the computation of 1,728 correlation coefficients.
• Accuracy versus series length.
• Accuracy versus classification entropy, where classification entropy is the Shannon entropy of the distribution of categories in a test set.
• Accuracy versus baseline accuracy, for each of the baselines.

Because of the large number of correlation analyses being performed, spurious low-level correlations were expected to be fairly numerous.

Also investigated was the number of algorithms necessary to achieve first rank or, separately, first or second rank at a given frequency on the particular set of test problems used here, with the hope that this would provide a rough indication of the number of algorithms one would have to employ to achieve nearly maximal performance on problems encountered in practice.

Results

Mean accuracy scores are shown in Table 2.  The horizontal line separates the baselines from the eight algorithms under investigation, all of which scored higher than the baseline methods.

Analysis of variance results were highly significant (F_11,12342=1008.86, P<0.001).  Pairwise comparisons identified several significant differences (Tukey HSD, q_inf,12>4.622, P<0.05), as shown in Figure 1.  The horizontal lines indicate groups that were not distinguishable.  In particular, note that POLY performed significantly better than all other algorithms, and GP and RAD performed significantly better than the remaining methods.  All algorithms performed significantly better than the baselines.

Results based on ranks were qualitatively similar.  As shown in Table 3, POLY had the best mean rank, followed again by GP and RAD.  Note that HMM ranked lower than the MAJ baseline.

Nonparametric ANOVA results were again highly significant (F_11,12342=965.09, P<0.001).  Pairwise comparisons are shown in Figure 2 (q_inf,12>4.622, P<0.05).  POLY and GP could not be distinguished based on ranks.  ARMA is now seen to rank significantly better than FS, TRE, and HMM, and NET ranks significantly better than TRE and HMM.  Note that HMM ranked more poorly than the MAJ baseline.

Figures 3, 4, and 5 show the relative accuracy scores when the analysis is performed separately by task type.  Although the results for Tasks 2 and 3 appear similar to the those presented above, those for Task 1 present some notable changes.  In particular, POLY, NET, HMM, and ARMA scored worse than the MAJ baseline, significantly so in the case of POLY, HMM, and ARMA.

Pairwise comparisons appeared to achieve a higher level of discrimination on Task 2 and especially on Task 3 than on Task 1, even though sample sizes were roughly equal (381 for Task 1, 373 for Task 2, and 369 for Task 3).

Ranks of all algorithms were highly variable, as shown in Table 4.  Nearly all algorithms ranked first and last at least once, and even two of the baselines (LIN and MAJ) ranked first at least once.

The frequency with which each algorithm achieved top rank on the problem set is shown in Table 5.  POLY and RAD are again seen to outperform the other methods, with POLY appearing at the very top of the list.  Note, however, that even POLY achieved top rank on only 42% of the problems.

Table 6 shows, for each group size, the maximal probability of achieving top rank on the problem set for any group of algorithms (of those included in this study) of that size.  As pointed out above, the best that a single algorithm can achieve is apparently 42%, and to achieve maximal score with at least 90% certainty would appear to require a group of at least 5 algorithms.

The analysis of Table 6 is generalized in Table 7 to the task of achieving first or second rank.  Once again, POLY is seen to outcompete the other methods, scoring very highly on a majority of problems.  Achieving first or second rank with at least 90% certainty appears to require a group of only 3 algorithms, and 4 algorithms provide a confidence of over 95%.

Relatively high correlations were found between the performance of some algorithms and that of one or more baselines.  It is interesting to note that POLY, the best performing algorithm used in this study, was also the least correlated to the baseline methods.  The closest competitors of POLY (GP and RAD) were, however, found to have appreciable correlations to baseline performance, in some cases in excess of 0.5.

Of the many correlation coefficients computed between algorithm performance and the various measures taken from the problems, even the most extreme appear to be of doubtful significance.  As shown in Table 9, most of these correlations, when taken as absolute values, fall below the 0.15 level, and none are above 0.18.  Give the large number of correlation coefficients computed (literally thousands), it seems reasonable to reject these low-level correlations as spurious.

measure               correlation     algorithm
problem size            -0.047      ;    GP
Hurst exponent           0.131          RAD  (task 3)
Lyapunov exponent       -0.131      ;    RAD  (task 2)
mean orbital period     -0.131          POLY (task 3)
embedding dimension     -0.087          NET  (task 1)
autocorrelation, lag 7  -0.172          ARMA (task 2)
classification entropy   0.046          NET
correlation dimension   -0.057          TRE
information dimension    0.059          FS
capacity dimension       0.093          FS

Table 9: Most extreme correlations found for various measures.

 
measure                  mean    stddev    min    max
classification entropy   1.46     0.46     0.15   2.25
problem size              487     1169       51  13292
hurst exponent           0.17     0.08    -0.06   0.45
lyapunov exponent        0.47     0.54    -0.01   2.22
mean orbital period      8.09     8.52        4    145
embedding dimension      4.19     3.76        2     20
correlation dimension    0.91     0.07     0.52   1.00
information dimension    0.92     0.04     0.71   1.00
capacity dimension       0.90     0.08     0.64   1.00

Table 10: Summary statistics for various measures.  stddev denotes standard deviation.

Discussion

A subsequent study [Majoros 2000b] found that NET could consistently outperform FS (i.e., according to all criteria used in that and the preceding study) if it was given copious computational resources, suggesting that the methodology of [Majoros 2000a] had introduced a bias against stochastic search algorithms, such as NET and GP.

In the present study, NET clearly failed to excel, quite possibly due to computational resource constraints.  Whereas [Majoros 2000b] provided 30 days of computing time to solve 38 problems, the present study provided only 4.5 days on the same hardware to solve 1,123 problems, or less than 1% of the level used in that earlier study.  Thus, NET may again be the victim of an unintentional (but largely unavoidable) bias against computationally intensive algorithms.

GP, however, performed well in all three studies, achieving in this study the second highest mean accuracy score and the second best mean rank.  This suggests that GP is a very reliable method for general problem solving, at least for classification tasks, despite its status as a potentially very resource intensive technique.

The most impressive algorithm investigated here, however, was POLY, which was not examined in the previous two studies (due to their atemporal nature).  POLY had the highest mean accuracy score and the best mean rank, and was able to both achieve top rank with greatest frequency and achieve first or second rank with greatest frequency.  POLY was followed in mean rank and mean score by RAD and GP, and thereafter by a larger group of largely indistinguishable methods (FS, NET, TREE, ARMA).

A different impression is given, however, by the task-specific analyses of accuracy scores, in particular those for Task 1.  On this subset, POLY failed to outperform even the MAJ baseline, as did also NET, HMM, and ARMA.  It is conceivable that POLY's poor performance on Task 1 was due to the small window size (5) on this task.  Larger windows were supplied only on the longer-term prediction tasks, under the assumption that low-frequency components of the signal would be less informative at the small scale of Task 1.  In retrospect, it is not clear that this was a valid assumption, especially for those series containing high-frequency noise.

POLY did, however, perform extremely well on Tasks 2 and 3, and can therefore be recommended for tasks involving categorical prediction at at least several time units in the future.

It is perhaps surprising that ARMA did not excel, given that it is such a popular method for time series work, and considering that the implementation used here consisted of published software written by an accomplished researcher in the field of signal processing [Masters 1995].  This failure might be attributable to the parameterization chosen for this model.  A single parameterization (4 AR terms and 1 MA term) was applied to all problems in this study, whereas a practitioner working on a single problem would likely investigate several parameterizations, and possibly even alternative (i.e., hybrid) ways of computing the  coefficients of the MA terms [Masters 1995].

This leads to a general criticism that could be fairly directed at the approach taken here and in other large-scale machine-learning experiments; namely, that in practice one should not expect exceptional performance from any blindly applied black-box algorithm, but that one should rather tailor an algorithm to the relevant properties of the particular system under study [Wolpert and Macready 1996].  This may involve a significant amount of exploratory data analysis, followed by development of a new algorithm or (possibly extensive) modification of an existing one.

This approach is simply not possible in a study involving 1,123 test problems without the expenditure of inordinate amounts of time.  Some effort was made, however, to mitigate the force of the above criticism by performing some automated analysis and preprocessing of the time series data and through automated searching of the parameter space of some of the models.  The unfortunate fact that the parameter space for ARMA was not effectively searched may have introduced a bias against this model, and this is an oversight that should be corrected in future studies.

Notwithstanding these arguments, there is still value in a large-scale study such as this one, because it addresses issues pertaining to the common practice of application by non-specialists of black-box algorithms to the everyday problems encountered in industry.  In particular, it supports results obtained in [Majoros 2000a] and [Majoros 2000b], where it was suggested that there is no "silver bullet" because the best algorithm (NET in the former study and FS in the latter) ranked first only 35%-41% of the time.  It was found here that POLY, which ranked first most frequently, did so only 42% of the time, so it appears that there is also no "silver bullet" for categorical time series prediction.  One might also go so far as to suggest that the greatest confidence one can have in any method for general problem solving is in the 40% range.  It would be interesting to find exceptions to this tentative rule.

In a more philosophical vein, another possibly informative aspect of a study like this is that it models to some degree the situation in nature where a complex adaptive system ("learner") must interact competitively with many different agents, which often cluster into a few "species," but which may still exhibit individualistic behavior.  Under these circumstances, the learner will likely be unable to dedicate significant resources to studying the behavior of an individual agent in the way that a researcher would study a particular system and manually build a highly specialized model for the prediction of that system's behavior.  For example, prey animals sometimes encounter the same individual predator repeatedly, but very often they are instead encountering different individuals.  Under such circumstances, the learner must rely on general learning mechanisms, to which our black-box algorithms may be seen as crude approximations.  Obviously, this observation is inapplicable to specialized mechanisms present in, for example, visual information processing circuitry and various other adaptive mechanisms possessed by organisms.

Caveats aside, it is interesting, on this interpretation, that GP performed so well, given that learners in nature are produced primarily through natural selection.  It would have been perhaps more interesting had NET also exhibited excellent performance.  As mentioned above, NET's failure to excel may be due to an inadequate search of the parameter space (i.e., synapse weights) for each problem.  It would be interesting to try combining NET and GP by evolving neural networks, as has been shown to be feasible by [Gruau 1996] and [Angeline 1997].

From a practical perspective, it is fortuitous that POLY exhibited such excellent overall performance, because the method is very easy to implement in software, and requires very little computational resources.  A naive implementation requires little more than procedures for matrix multiplication and inversion, which are described in virtually every linear algebra textbook.

Another simple method which turned out to work surprisingly well was RAD.  This algorithm performed nearly as well as POLY on Tasks 2 and 3, and it produced the best mean score on Task 1, on which POLY performed poorly.  The success of this method may be attributable to the surprising power of attractor reconstruction [Strogatz 1994].  This view is lent additional support by the excellent performance of FS (which also employs attractor reconstruction) on Task 1.

The performance of HMM was disappointing -- it actually ranked lower than the MAJ baseline.  Hidden Markov models are known to be very effective on some applications, such as gene-finding and protein structure prediction [Durbin 1999].  It is quite possible that HMM performed poorly in the present study because of the discretization of the inputs -- the only other method used here which discretized inputs was TRE, and that method also failed to excel.

One of the goals of [Majoros 2000a] was to identify groups of algorithms ("toolkits" or "arsenals") that would suffice to produce nearly maximal accuracy on real classification problems (where maximal was defined relative to the particular set of algorithms used in that study).  It was concluded that a fairly large arsenal (5 to 7 algorithms) was required to consistently rank highest, although a somewhat smaller toolkit (3 to 4 algorithms) could consistently rank nearly best (i.e., achieve 1^st or 2^nd rank).  [Majoros 2000b] apparently reduced the toolkit size required for consistently ranking best by providing 100 times more computing power.

Results of the current study are more similar to those of [Majoros 2000a] in that 5 to 6 algorithms were required to consistently score highest in the context of the current problem set and the competing algorithms.  The results of [Majoros 2000b] might have been approached had NET and GP been given similar computational resources, but that would have required 29 months of compute time on the hardware available for this study (8 Pentium III processors running at 800MHz).

In general , no correlations were found between any of the complexity measures and the accuracy scores of any of the algorithms.  Indeed, as Kantz and Schreiber have noted,

the interpretation of [Lyapunov exponents, etc.] as measures of 'complexity' of the underlying systems has met with increasing criticism.  It is now quite generally agreed that, in the absence of clear scaling behavior, quantities derived from dimension or Lyapunov estimators can be at most relative measures of system properties.

a scaling range will always have to be determined by inspection.  Even data sets from the same experiment can vary so strongly in their geometrical structure that we cannot recommend the use of any automated procedure to determine...the correlation dimension.

It is interesting to note that POLY, the algorithm producing the best overall accuracy scores, was also the least correlated to the baseline methods.  The closest competitors of POLY (GP and RAD) were, however, found to have appreciable correlations to baseline performance, in some cases in excess of 0.5.

The prediction tasks used in this study were somewhat unconventional in that they were categorical.  This allowed the (re)use of classification algorithms for time series prediction, and served as a way to test conclusions drawn in [Majoros 2000a] and [Majoros 2000b] regarding the use of black-box algorithms for classification.

However, the potential for categorical prediction is actually quite relevant in some domains.  In order to decide whether to buy or sell a given stock, it is generally only necessary to predict whether the stock will rise or fall by at least a certain amount, over a certain time.  This is certainly true for those who need to turn a certain profit each month in order to cover expenses.  It may also be true in a wide variety of circumstances in nature, where an organism must predict whether its environment is likely to change qualitatively in the near future.

It should be noted that most of the time series used in this study were taken from real systems, many of them either physical (river levels, chemical concentrations) or economic (stock prices, daily wages).  Only a very few of the series were described as having been generated artificially using nonlinear equations.  For this reason, the problems used here should be viewed as representative of problems encountered in the real world, rather than as "toy" problems.
 
 

Conclusion

Polynomial regression was seen to perform particularly well on categorical prediction tasks involving lead times of at least several time units.  Due to its remarkable ease of implementation and minimal resource requirements, this method can be recommended to anyone having considerable resource and/or development constraints.

As previous studies have done, however, it was advised that prospective practitioners expecting to regularly encounter a variety of classification tasks accumulate a "toolbox" of 4 to 6 standard techniques, perhaps including polynomial regression, radial basis functions, neural networks, and genetic programming.  These methods can all be applied to novel prediction problems as they arise, with the most competitive algorithm on the training set being selected for deployment.

References

[Durbin 1999] Richard Durbin, et al., Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids, Cambridge University Press, 1999.

[Gruau 1996] Frederic Gruau, Darrell Whitley, and Larry Pyeatt, "A Comparison between Cellular Encoding and Direct Encoding for Genetic Neural Networks," in Proceedings of the First Annual Conference on Genetic Programming, pp. 81-89, MIT Press, 1996.

[Kantz and Schreiber 1997] Holger Kantz and Thomas Schreiber, Nonlinear Time Series Analysis, Cambridge University Press, 1997.

[Liebovitch and Toth 1989] Liebovitch and Toth, "A Fast Algorithm To Determine Fractal Dimensions By Box Counting", Physics Letters A, p141, pp386-390, 1989.

[Majoros 2000a] Bill Majoros, "On Free Lunches and Silver Bullets: An Empirical Comparison of Seven Machine-Learning Algorithms for Classification," <http://geocities.datacellar.net/ResearchTriangle/Forum/1203/ml_7.html>, June 2000.

[Majoros 2000b] Bill Majoros, "Clock Cycles Versus Inductive Bias: An Empirical Comparison of Classification Algorithms under Varying Computational Resource Constraints," <http://geocities.datacellar.net/ResearchTriangle/Forum/1203/ClockCycles.html>, December 2000.

[Masters 1995] Timothy Masters, Neural, Novel & Hybrid Algorithms for Time Series Prediction, John Wiley & Sons, 1995.

[Peters 1996] Edgar Peters, Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility, John Wiley & Sons, 1996.

[Strogatz 1994] Steven H. Strogatz, Nonlinear Dynamics and Chaos, with Applications to Physics, Biology, Chemistry, and Engineering, Addison-Wesley, 1994.

[Wolf 1985] A. Wolf, J. B. Swift, et al., "Determining Lyapunov Exponents from a Time Series." Physica D 16, pp285-317,  1985.

[Wolpert and Macready 1996] David H. Wolpert and William G. Macready, "No Free Lunch
Theorems for Search," Santa Fe Institute Technical Report #SFI-TR-95-02-010, 1996.

[Zar 1996] Jerrold H. Zar, Biostatistical Analysis, Prentice Hall, 1996.
 

REFERENCES FOR DATA SETS ONLY

Most of the data sets can be freely downloaded over the internet.  Original references are given below, rather than URL's.  The appropriate URL's can be found by entering author names and other relevant keywords into an internet search engine, such as Alta Vista (http://www.altavista.com).

Abraham and Ledolter, Statistical Methods for Forecasting, Wiley, 1983.

Anderson, O.D., Time Series Analysis and Forecasting: the Box-Jenkins Approach, Butterworth, 1976.

Anderson, T.W., The Statistical Analysis of Time Series, Wiley, 1971.

Andrews, D.F. and H.M.Herzberg, Data: A Collection of Problems from Many Fields for the Student and research Worker, Springer-Verlag, 1985.

Box, Hunter, and Hunter, Statistics for Experimenters, pp32-33, Wiley, 1978.

Box, G.E.P. and G.M. Jenkins, Time Series Analysis: Forecasting and Control, Holden-Day, 1976.

Carey, J. R. et al., "Slowing of Mortality Rates at Older Ages in Large Medfly Cohorts," Science 258, pp457-461, 1992.

Carnegie Mellon University Department of Statistics, StatLib, http://lib.stat.cmu.edu

Cobb, George W., "The problem of the Nile: Conditional solution to a changepoint problem," 78Biomtrka65, pp243-252.

Davies, P.L. and Gather, U., "The identification of multiple outliers," Journal of the American Statistical Association 88, pp782-801, 1993.

Diggle, P., Time Series: A Biostatistical Introduction, Oxford University Press, 1990.

Hansen, James and Sergej Lebedeff, "Global Trends of Measured Surface Air Temperature," Journal of Geophysical Research 92(D11), pp 13,345-13,372, November 20, 1987.

Harvey, A., Forecasting, Structural Time Series Models and the Kalman Filter, CUP,  1989.

Hipel, K.W. and A.I. McLeod,  Time Series Modeling of Water Resources and Environmental Systems, Elsevier, 1994.

International Institute of Forecasters, The M3 Competition, http://forecasting.cwru.edu/data.html

Kendall, M.G., Time Series, Griffin, 1973.

Lange, Nicholas et al., Case Studies in Biometry, John Wiley & Sons, 1994.

Makridakis, Wheelwright and Hyndman, Forecasting: Methods and Applications, 3rd ed, Wiley, 1998.

McCleary and Hay, Applied Time Series Analysis for the Social Sciences, Sage Publications, 1980.

McLeod, A. Ian, "Parsimony, Model Adequacy and Periodic Correlation in Time Series Forecasting," ISI Review, 1992.

Montgomery and Johnson, Forecasting and Time Series Analysis, McGraw-Hill, 1976.

Morettin, P.A., A.R. Mesquita, and J.G.C. Rocha, "Rainfall at Fortaleza in Brazil Revisited," Time Series Analysis, Theory and Practice, Vol. 6. pp67-85.

National Oceanic and Atmospheric Administration National Centers for Environmental Prediction, Surface Marine Data, ftp://ftp.cdc.noaa.gov/Public/coads/ncep_obs/README

National Oceanic and Atmospheric Administration National Ocean Survey, Great Lakes Water Levels, 1860-1986,  U.S. Dept. of Commerce

Nelson, Applied Time Series Analysis for Managerial Forecasting, Holden-Day, 1973.

O'Donovan, T.M, Short term Forecasting: An Introduction to the Box-Jenkins Approach, Wiley, 1983.

Percival, D. B., "Spectral Analysis of Univariate and Bivariate Time Series," in Statistical Methods for Physical Science, edited by J. L. Stanford and S. B. Vardeman, Academic Press, 1993.

Percival, D. B. and P. Guttorp, "Long-Memory Processes, the Allan Variance and Wavelets", in Wavelets in Geophysics, edited by E. Foufoula-Georgiou and P. Kumar, Academic Press, 1994.

Percival, D. B. and A. T. Walden, Spectral Analysis for Physical Applications, Cambridge University Press, 1993.

Pankratz, A., Forecasting With Univariate Box-Jenkins Models: Concepts and Cases, Wiley, 1983.

Pankratz, A., Forecasting With Dynamic Regression Models, Wiley, 1991.

Subba Rao, T. and M.M. Gabr, An Introduction to Bispectral Analysis and Bilinear Time Series Models, Springer-Verlag, 1984.

Tong, H., Non-linear time series: a dynamical systems approach, Oxford University Press, 1991.