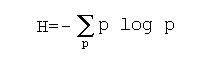
Abstract
However, it is generally recognized that the No Free Lunch theorems do not strictly apply in practice because real-world problems are a biased sample of the set of all possible problems. For example, many of the problems of practical interest involve the behaviors of biological systems. Because of the highly biased nature of the evolutionary processes shaping these systems, it is difficult to justify treating these problems as a random sample of the set of all possible mathematical constructions (notwithstanding the existence of deterministic chaos -- but see [Kauffman 1993] for some relevant speculation).
Thus, it is not surprising that some algorithms appear to perform better on average than random guessing.
However, there is a tendency among many scientists and engineers to have one "favorite" algorithm, which they apply to the exclusion of all other techniques. These include such simple methods as multiple regression and the naive Bayes classifier, as well as more sophisticated models such as neural networks and genetic algorithms.
In this study, I tested a set of twelve variants of seven of these popular algorithms on a suite of 38 problems in order to determine whether any one algorithm was sufficient to produce high accuracy scores on nearly all of the problems.
I also subdivided the problem set according to various properties of the problems and tested all of the algorithms on each of the subsets, in order to investigate to what degree a problem's properties can profitably guide the algorithm selection process.
Finally, I considered the "coverage" of the problem set that would be achieved by various groups of algorithms, in order to determine how large a standard "toolbox" of methods would have to be in order to be highly confident that maximal accuracy will be achieved by at least one algorithm in the toolbox.
A classification task involves the assignment of each incoming object to one of several classes, or categories. During training, the learner has access to both the object's attributes, or features, and its true category. During testing, it has access only to the attributes, and is expected to accurately predict the object's class.
Nine artificial problems (monk1-3 and nl1-6) and 29 real-world problems were used to evaluate the algorithms. Seven of the problems (monk1-3, vote, soybean, crx, and hypo) were taken from the R5 distribution of Quinlan's C4.5 software [Quinlan 1993]. Six problems (nl1-6) were artificial problems generated for this study; these were implemented as C++ programs that generated random inputs and categorized them by using various algebraic expressions (see Appendix A). The rest were taken from the machine learning repository at the University of California at Irvine [Murphy and Aha], and are briefly described below.
Problem sizes are shown in Table 1.
problem
classes nominal numeric training testing
ocr
26 0
16 15000 5000
income
2 6
8 7000 3000
pendigits
10 0
16 7494 3498
optdigits
10 0
64 3823 1797
bands
2 19
20 275
275
ind-diabetes 2
0 8
384 384
dermatology 6
0 34
183 183
mushroom
2 22
0 4000 4124
haberman
2 0
3 153
153
liver
2 0
5 245
100
tae
3 4
1 76
75
glass
7 0
9 107
107
wine
3 0
13 89
89
water-treatmt 13
0 38
300 223
vote
2 16
0 300
135
soybean
19 35
0 340
345
crx
2 9
6 490
200
hypo
5 23
6 2514 1258
ionosphere
2 0
34 200
151
problem
classes nominal numeric training testing
hepatitis
2 13
6 75
80
brst-cancer 2
0 9
350 349
ecoli
8 0
7 150
186
iris
3 0
4 75
75
yeast
10 0
7 742
742
abalone
29 1
7 2000 2177
mpg
3 3
4 200
192
scale
3 0
4 300
325
cmc
3 3
6 700
773
echocardio
2 1
5 66
66
monk1
2 6
0 124
432
monk2
2 6
0 169
432
monk3
2 6
0 122
432
nl1
2 0
4 400 1000
nl2
2 0
4 400 1200
nl3
2 0
4 400 1200
nl4
2 0
4 400 1200
nl5
2 0
4 400 1200
nl6
2 0
4 400 1200
Table 1: Number of classes, number of nominal and numeric attributes,
and sizes of training and test sets of problems used in this study.
Note that for problems having only one data set, that set was randomly shuffled and split into two sets of roughly equal size. Thus, each learner was trained using a training set and then evaluated on a separate test set. This tests the ability of the learner to classify objects not encountered during training, and gives a measure of its ability to infer a general model that accurately reflects the structure of the entire space from which the training sample was drawn (i.e., to generalize).
Most of the algorithms were trained on the same training sets and tested on the same test sets. However, due to the limited amounts of computing resources available, some of the more compute-intensive algorithms were trained and/or tested on reduced data sets for the larger problems. These reduced sets were produced by random sampling of the standard training/test sets to produce data sets small enough to be processed by the algorithm in an amount of time comparable to that used by the other methods.
For this reason, the results reported here will be somewhat biased against the more resource-intensive algorithms, such as genetic programming and K-nearest-neighbors. This bias may be justified if one is concerned with the performance of these algorithms in circumstances where computing resources are limited.
Most of the analyses will involve only the real-world
problems; scores on the artificial problems will be used occasionally to
increase sample size.
II. THE ALGORITHMS
All seven algorithms were coded from scratch in C++, compiled using the gnu g++ compiler version 2.91.60, and executed on Caldera Linux 2.2 running on a 466 MHz Celeron with 96 MB of RAM.
All algorithms accepted their input files in a single standard format similar to that employed by the C4.5 program [Quinlan 1993]. This greatly facilitated rapid comparison of many algorithms on many problems.
A short description of each algorithm is given below. For a more detailed treatment of these methods, see [Quinlan 1993, Mitchell 1997, Koza 1992, Hassoun 1995, Manly 1994]. Each section heading also includes one or more abbreviations in parentheses that will be used throught this paper.
A. Neural Networks (NET)
A neural network is a collection of memory cells called neurons, which are arranged into some topology by connections called synapses. A single synapse connects two neurons, and allows the current state of one neuron to influence the next state of the other neuron. The magnitude of this influence is determined in each case by the weight of the synapse in question. Each neuron has a set of incoming synapses, and the signals on these synapses are mapped by a transfer function to a new state value for the neuron.
In this way, signals can propagate from the neurons on the left of the network to those on the right. The leftmost neurons are input neurons, which receive the problem description, and the rightmost neurons are output neurons, which are expected to produce a solution to the problem. All other neurons are called hidden nodes, and are generally organized into layers called hidden layers, where all the neurons in a layer are the same distance (measured by shortest path length) from the inputs.
Backpropagation is one of several algorithms commonly used to train a neural network (i.e., to select appropriate synaptic weights). It works by applying input values to the network, propagating the signals through to the output neurons, and comparing the actual result to the expected result. The difference between the actual and expected results is the error, which is then propagated backward through the network in order to assign blame to specific synapses for the error, and to modify the synaptic weights to reduce this error. This is performed repeatedly, in hopes that the system will converge toward an approximately correct model.
Thus, backpropagation attempts to minimize error, and it does this by using a form of hill-climbing, which unfortunately tends to find only local minima. To try to find the global minimum, one can randomize the synaptic weights at the start of training, and repeat the process several times in order to better explore the search space.
All neural networks in this study were trained using the backpropagation algorithm. For the transfer function I used the logistic function, 1/(1+e-s), where s is the sum of inputs to the neuron and e is the Euler number. Synaptic weights were initialized to small random values (-0.05 to 0.05) at the beginning of each run, as suggested by [Mitchell 1997].
Neurons were organized into layers, as described above, except for a special bias node, the output of which fed into all other neurons (except those in the input layer). Each node in a layer was connected to every node in the next layer. The output layer consisted of one neuron per category, with the most active output neuron determining the prescribed categorization. Inputs were linearly scaled to lie between 0 and 1.
Nominal attributes were decoded into a 1-out-of-n representation (i.e., an attribute assuming one of n unordered values was represented by n binary variables constrained to contain n-1 zeros and one 1). Additional runs were also performed without this decoding (i.e.,using arbitrary integer codes), and the better score from these two representations was recorded.
For each problem, backpropagation was performed under varying parameterizations in order to maximize performance. This typically involved 10 or 20 runs for each problem. The process started with simple topologies (1 hidden layer containing 1 node) and small numbers of iterations (10 or 20) and proceeded to explore progressively more complex and time-consuming parameterizations. Each dimension of the parameterization was varied slightly in each direction until a clear pattern of decreasing performance was observed. The best performance was typically achieved using one hidden layer of 1 to 10 nodes, and typically required 10 to 200 iterations.
For more information on neural networks, see [Mitchell 1997, Hassoun 1995].
B. Decision Trees (TRE)
A decision tree is a data structure that can be used to classify objects by following a path through the tree from the root to one of the categories at the leaves. Each internal node of the tree tests an attribute of the object and directs the object to one of its subtrees based on the results of that test. Each leaf node assigns objects to exactly one class. Thus, objects flow from the root to the leaves, with different objects flowing along (potentially) different paths.
Induction of decision trees from a training set can be achieved by applying a criterion based on the information-theoretic measure called entropy. The entropy of a distribution is a measure of the uncertainty of the outcome of an event known to follow the distribution. It is defined as
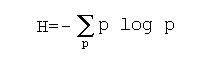
In J. R. Quinlan's popular C4.5 algorithm [Quinlan 1993, 1986], an entropy criterion is used to minimize the height of the decision tree by stipulating that each internal node must reduce the entropy of classification as much as possible. The algorithm begins at the root and progressively grows the tree downward. When adding a new internal node, the algorithm considers all possible attribute tests that could be performed at that node, and evaluates the entropy reduction that the test would achieve. The test that achieves the greatest entropy reduction is selected at each node, and this continues until a certain level of certainty about the classification has been reached. At this point, a leaf node is created which simply assigns objects to the majority class of the distribution of training cases that flow down to that leaf.
Unfortunately, although C4.5 compiled fine on Linux, it malfunctioned on all of the test sets provided with the C4.5 package, so a similar decision tree program was written and used in place of C4.5 for this study.
The algorithm used herein performed only binary tests on attributes, so that the decision trees were binary trees. A test on a nominal attribute was of the form attribute==value, and a test on a numeric attribute was of the form attribute<=value. Test values for numeric attributes were selected by sorting the values observed in the training set, uniformly reducing the size of this value set if it was very large, and then averaging adjacent pairs of the remaining values.
The tree was inferred in a top-down manner, and stopped when entropy reduction reached a specified threshold. This threshold is the only parameter to the algorithm. For each problem, the algorithm was executed initially with a threshold of 0.5, and was repeated for nearby values (i.e., 0.4 and 0.6, then 0.3 and 0.7) until a clear pattern of decreasing performance was observed.
Gain ratio [Quinlan 1986] was not employed.
The algorithm used in this study was briefly compared to the C4.5 algorithm by running it on a subset of the classification problems (see below). For this part of the study, C4.5 was executed on a Sun Sparcstation running Solaris.
C. Naive Bayes Classifier (BAY)
The Naive Bayes Classifier [Mitchell 1997] is a simple method based on a well-known result called Bayes' Theorem. It utilizes the following formula:
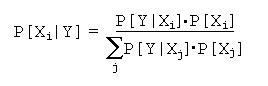
Once the joint probabilities are known, the probability of each category can be computed for a given test case. That case is then assigned to the most likely category.
This method has no parameters, except for the discretization of numeric attributes, which, for the present study, was done by discretizing each numeric attribute into 20 equal-sized intervals. This parameter was not varied during the study.
D. K-Nearest-Neighbors (KN,KNW,MAH,KWM,FS)
The nearest-neighbor technique simply computes a distance metric between a test case to be classified and every training case seen during the training phase, and then assigns the test case to the same category as contains the closest training case.
K-nearest-neighbors is a generalization of this which finds the K training cases nearest the test case and then assigns the case to the most frequently occurring category among those K neighbors. In this study, frequency was weighted by closeness to the test case:
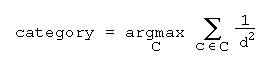
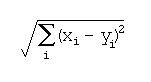
In addition to the simple K-nearest-neighbors algorithm
just described, four additional variants were tested:
1. K-nearest-neighbors with Feature Selection (FS)This variant uses a stepwise procedure to select a subset of the attributes to use in the computation of distance. All attributes were sorted according to their F ratio, where F ratio=MSgroup/MSerror is the ratio of between-group variance to within-group variance, and is a measure of the ability of the attribute to separate groups [Zar 1996]. Attributes were successively considered in order of increasing F ratio. Each attribute under consideration was dropped from the model and the accuracy recomputed using cross-validation (random 2/3 of the training set used for training and the remaining 1/3 used for testing). If dropping the attribute resulted in decreased accuracy, the attribute was restored and the stepwise procedure terminated.2. K-nearest-neighbors with Weighted Attributes (KNW)As with feature selection, this variant computes an F ratio for each attribute, but rather than dropping attributes with low F ratio, it simply weights the contribution of the attribute to the distance computation by dividing the corresponding distance component by the F ratio.3. K-nearest-neighbors using Mahalanobis Distance (MAH)This variant uses Mahalanobis distance rather than Euclidean distance to find the nearest neighbors. Mahalanobis distance is similar to Euclidean distance, except that the distance components are multiplied by the inverse covariance matrix of the attributes in order to control for multicolinearity [Manly 1994]. Multicolinearity occurs when two or more attributes are correlated, and results in distances that are biased by the redundancy of the correlated features. Mahalanobis distance corrects for this bias.
4. K-nearest-neighbors using Mahalanobis Distance with Weighted Attributes (KWM)All of these variants take a single parameter, K. For problems with a reasonably small number of training cases, K was varied between 1 and 30, inclusive. For larger data sets, several K values between 1 and 30 were sampled, to save time, since this algorithm runs very slowly for large data sets.This variant simply combines the previous two variants by utilizing both Mahalanobis distance and the weighting of attributes by their F ratios.
E. Nearest-Centroid (NC,NCM)
The nearest-centroid method (NC) is similar to the nearest-neighbor method, except that the centroids (average position) of all cases in each category are computed, and the test case is assigned to the category of the nearest centroid.
A variant of the nearest centroid method (NCM) uses Mahalanobis distance.
F. Regression (REG)
Multiple linear regression was used to classify the test cases by taking the encoded category as the response variable (Y) and the attributes as the predictor variables (Xi), and performing regression on the training set to produce a set of linear functions. Each linear function was associated with a pair of categories, and was used to discriminate between those two categories by interpreting a Y value of less than or equal to 0.5 as assignment to the one category and greater than 0.5 as assignment to the other. In order to classify a new case, all of the linear functions were evaluated, producing a count of "votes" for each category. The case was then assigned to the category with the most votes.
Decoding of nominal attributes into a 1-out-of-n representation, as described above for neural networks, was not used, because on every problem having at least one nominal attribute, the decoded representation either produced poorer results or gave rise to a noninvertible matrix, making regression impossible. In addition, standardization of numeric attributes (by subtracting the mean and dividing by the standard deviation) produced no improvements in accuracy in preliminary trials involving a subset of 13 problems (data not shown), so the transformation was not applied during the experiment.
G. Genetic Programming (GP)
Genetic programming [Koza 1992] is the application of a genetic algorithm to syntax trees representing executable programs. For classification, each syntax tree can be considered a classification algorithm. We begin with a population of randomly generated syntax trees, and we test each tree's ability to classify the training cases.
Each tree is allowed to survive and reproduce with probability proportional to its fitness (classification ability). Reproduction consists either of cloning (20%), mutating (40%), or engaging in crossover (40%). Mutation involves replacing a randomly chosen node in (a copy of) the tree with a new randomly chosen node, with the children of the old node then being copied over to be the children of the new node. Crossover between two individuals involves randomly swapping one pair of subtrees between (copies of) the individuals.
The relative proportions of these genetic operators were chosen somewhat arbitrarily, because experimental evidence suggests that crossover and mutation are often equally effective at promoting adaptation [Angeline 1997, Luke and Spector 1997, Chellapilla 1997]. In addition to these operators, a low level (1%) of immigration occured, whereby randomly-generated individuals were added to the population in an attempt to replenish diversity lost to genetic drift [Falconer and Mackay 1996].
Individuals were selected for reproduction using tournament selection, in which several individuals (usually four to seven) are chosen uniformly at random to participate in a tournament that they will win with probability proportional to their fitness [Koza 1992].
For the purposes of this study, each individual actually consisted of a value-producing tree and one or more automatically defined functions (ADF), each of which is simply a separate syntax tree. An individual is exercised by evaluating the value-producing tree, which may contain calls to any of the individual's ADF's. An ADF may contain calls to other ADF's or even recursive calls to itself. To prevent infinite recursion, the call stack for an individual was limited to a fixed maximum depth of ten activation records.
Each individual was exercised on a random sample of the training set. The sample size was varied between runs, and was typically 30%-70% of the size of the training set. After three-fourths of a run had been completed, the sample size was automatically increased to 100%.
Terminals (nodes at the leaves of the tree) were either randomly generated constant real values in the range -10 to 10 (33%) or a randomly selected feature of the test case (67%). Nonterminals (interior nodes; operators) were chosen from the following set of operators:
(1) +,-,*,/,&&,||,!=,==,>,>=,<,<=,!,?:,
(2) exp,sin,cos,log,fabs,ceil,sinh,cosh,atanh,asinh,acosh,
cbrt,sqrt,atan,asin,acos,tan,hypot,
(3) log2,log10,fmod,min,max,ifgz,call,^
The first line consists of the usual C++ operators, and the second line contains functions commonly found in the standard C++ libraries. In the third line, log2 and log10 are the binary and common logarithms, respectively, fmod is fractional remainder after floating-point division, min and max return the smaller and larger (respectively) of their two parameters, ifgz(x,y,z) is equivalent to (x>0 ? y : z), call(f) is a call to ADF number f, and ^(x,y) denotes xy.
The trees in the initial population were generated to be between 2 and 4 nodes deep, inclusive. No maximum depth was enforced during execution, although time constraints (see below) may have placed an effective limit on depth due to the time cost incurred by executing deeper trees (i.e., terminating a run which is progressing very slowly due to tree size amounts to group selection against populations of large trees). Some form of depth control is usually necessary in genetic programming, because syntax trees naturally tend to grow without bound over the course of evolution, without necessarily experiencing a concomitant increase in fitness [Soule, et al. 1996, Langdon and Poli 1997] (but see [Soule and Foster 1998]).
Note that mutation occasionally replaced an operator with another operator of different arity (number of parameters). To accommodate this possibility, requests for subtree values by an operator were specified using the subtree index, and these indices were taken modulo the number of subtrees actually present (which was never zero for a nonterminal).
The population size was held constant by eliminating all individuals of the current generation after reproduction. The population size was typically set to 100 initially, and then changed to 200 to see whether a larger population was needed. If the larger population performed better, larger populations up to 1000 were tried. Likewise, the algorithm was typically run for 100 generations, and then longer runs were performed if additional generations appeared to improve performance.
However, both of these parameters were subject to the constraint that no individual run take longer than approximately 30 minutes of wall-clock time, and no problem may consume more than approximately 60 minutes total wall-clock time for all runs of the algorithm. In general, several short runs were preferred over one long run, because previous experience dictated that such a strategy tended to produce better results [unpublished data; also Gathercode and Ross 1997].
It should be noted that the hardware used in this study was extremely minimal relative to the resource requirements of GP. Some of the more successful applications of GP to real problems have involved the use of far superior computing facilities (for example, a 64-node PowerPC cluster processing a combined population size of 640,000 -- see [Koza, et al. 1997a and 1997b]).
H. Baselines (MAJ,RND)
For the purpose of comparison, two baseline methods were assumed. The first is the majority rule (MAJ), which simply assigns all objects to the most frequently occurring class in the training set. The accuracy of this baseline is taken to be the percentage of objects in the test set belonging to that class.
The second baseline is the random guess (RND); objects
are classified by randomly picking categories according to a uniform distribution.
The expected accuracy of 1/n, where n is the number of categories, was
used as the accuracy for this baseline.
III. STATISTICAL ANALYSES
To test the prediction of the No Free Lunch theorems that all algorithms would perform similarly to random guessing, analysis of variance (ANOVA) was applied to the randomized block design obtained by treating algorithms as treatments and problems as blocks. Pairwise comparisons were performed using the Tukey test. This analysis was performed both on the entire suite of problems and on the subset of 29 real-world problems, and was applied both to scores and to ranks, to produce four separate analyses.
To detect sensitivities of algorithms to various properties of tasks in the problem set, linear correlation coefficients (r) were computed between accuracy scores for an algorithm and corresponding task attributes. The task attributes considered were: number of categories, number of training cases, number of test cases, number of attributes, and the proportion of attributes that were nominal. Scores for all 38 problems were included in the analysis.
Pairwise comparisons between correlation coefficients were performed by simply comparing pairs of coefficients independently, rather than using the Tukey-type comparison suggested by [Zar 1996], because the statistical power involved was already quite low.
In addition, the mean rank of each algorithm was computed separately on eight subsets of the problems. The subsets consisted of those problems having:
Observed frequencies of achieving the best and second best ranks on real-world problems were tabulated for all algorithms, and for all possible groups of algorithms.
Because C4.5 could not be executed in the test environment, the replacement algorithm for inducing decision trees was compared to C4.5 by running both algorithms on a subset of the classification tasks (vote, soybean, crx, hypo, monk1, monk2, and monk3) and subjecting the accuracy scores to the Wilcoxon paired-sample test.
Ranks were computed by ordering the algorithms by decreasing accuracy scores, assigning indices starting at 1, and then averaging indices associated with tied scores to produce ranks. All significance levels were set at 0.05. All tests and analyses were performed using unpublished software written by the author, except for the Wilcoxon paried-sample test, which was performed using SPSS. All manually coded statistical procedures followed [Zar 1996].
The accuracy scores are presented in Table 2. Each score represents the percentage of the test cases that the algorithm classified correctly. A value of "ni" indicates that the algorithm could not be run because a matrix utilized by the algorithm was found to be noninvertible.
The algorithms are abbreviated as follows: RND=random guessing, MAJ=majority rule, BAY=naive Bayes classifier, NET=neural network, TRE=decision tree, NC=nearest centroid with Euclidean distance, KN=K-nearest-neighbors, FS=K-nearest-neighbors with feature selection, MAH=K-nearest-neighbors using Mahalanobis distance, KNW=K-nearest-neighbors with weighted attributes, KWM=K-nearest-neighbors using Mahalanobis distance with weighted attributes, NCM=nearest-centroid using Mahalanobis distance, REG=linear regression, and GP=genetic programming.
problem
RND MAJ BAY NET TRE NC KN FS MAH KNW KWM NCM REG GP
ocr
4% 4% 75% 59% 86% 58% 84% 89% 85% 56% 47% 66% 82% 8%
income
50% 76% 77% 85% 83% 55% 71% 73% 78% 70% 74% 79% 82% 80%
pendigits 10% 10% 79% 54%
94% 78% 97% 97% 96% 96% 96% 82% 95% 23%
optdigits 10% 10% 73% 69%
86% 89% 97% 98% ni 96% ni ni ni 24%
bands
50% 51% 51% 74% 69% 67% 72% 72% ni 79% ni ni 51% 74%
ind-diabetes 50% 64% 61% 68% 73% 65% 74% 76%
75% 69% 63% 76% 78% 76%
dermatology 17% 31% 53% 98% 97% 45% 87%
98% 84% 52% 74% 96% ni 63%
mushroom 50% 52% 100%100%99%
64% 100%100% ni 100% ni ni 79% 99%
haberman 50% 68% 69%
68% 73% 75% 71% 72% 71% 65% 65% 62% 68% 76%
liver
50% 49% 50% 64% 61% 67% 58% 60% 54% 63% 55% 64% 64% 67%
tae
33% 27% 55% 61% 60% 43% 53% 53% 59% 55% 57% 63% 52% 40%
glass
14% 31% 49% 43% 64% 40% 69% 69% 64% 62% 54% 58% ni 60%
wine
33% 36% 39% 98% 93% 71% 69% 71% 97% 67% 81% 98% 99% 88%
water-treatmt 8% 48% 48% 62% 66% 18% 55% 63%
56% 53% 57% 68% ni 48%
vote
50% 61% 79% 97% 97% 88% 89% 96% 93% 89% 80% 95% 96% 99%
soybean
5% 13% 82% 91% 85% 51% 60% 84% 88% 60% 72% 89% ni 16%
crx
50% 55% 65% 86% 82% 67% 66% 73% 83% 65% 65% 84% 84% 84%
hypo
20% 92% 95% 94% 97% 0% 96% 96% ni 94% ni ni ni
93%
ionosphere 50% 82% 95% 96% 97%
62% 95% 94% ni 91% ni ni ni 97%
problem
RND MAJ BAY NET TRE NC KN FS MAH KNW KWM NCM REG GP
hepatitis 50% 81% 80% 81%
83% 68% 74% 78% 83% 76% 80% 76% 76% 85%
brst-cancer 50% 66% 95% 97% 94% 96% 97%
97% 93% 97% 93% 96% 96% 97%
ecoli
13% 39% 40% 72% 80% 81% 86% 86% ni 85% ni ni ni
59%
iris
33% 31% 97% 93% 97% 97% 100%100%89% 96% 81% 84% 96% 99%
yeast
10% 27% 27% 49% 52% 48% 59% 59% 56% 54% 52% 47% ni 34%
abalone
3% 17% 21% 23% 23% 6% 26% 24% 22% 25% 19% 22% ni 17%
mpg
33% 45% 50% 85% 80% 70% 77% 78% 81% 76% 81% 78% 82% 77%
scale
33% 46% 90% 93% 79% 72% 92% 92% 91% 92% 90% 73% 89% 100
cmc
33% 40% 48% 56% 51% 39% 53% 53% 48% 51% 47% 47% 50% 42%
echocardio 50% 82% 79% 82% 82%
56% 76% 77% 79% 79% 80% 68% 82% 85%
monk1
50% 50% 71% 86% 93% 50% 70% 75% 73% 70% 62% 52% 52% 83%
monk2
50% 67% 62% 71% 87% 67% 79% 78% 68% 80% 72% 51% 67% 67%
monk3
50% 47% 97% 81% 97% 64% 67% 89% 84% 67% 63% 76% 77% 97%
nl1
50% 51% 85% 99% 87% 93% 96% 96% 95% 96% 95% 98% 98% 96%
nl2
50% 59% 89% 90% 91% 88% 92% 92% 91% 81% 82% 88% 89% 89%
nl3
50% 60% 76% 85% 79% 79% 89% 89% 86% 71% 70% 79% 79% 76%
nl4
50% 52% 82% 89% 85% 89% 90% 92% 89% 69% 69% 91% 90% 90%
nl5
50% 52% 83% 83% 82% 81% 82% 83% 81% 56% 54% 81% 82% 83%
nl6
50% 50% 88% 85% 91% 92% 91% 92% 89% 49% 48% 92% 92% 90%
Table 2: Accuracy scores. See text for abbreviations.
Table 3 gives the means and standard deviations of algorithm
ranks on the real-world problem set. The variances appear to be fairly
similar.
alg mean
sd
FS 4.33
2.85
NET 4.45
3.07
TRE 4.57
2.29
KN 5.45
3.46
GP 5.93
3.98
KNW 6.74
3.19
MAH 7.00
3.42
NCM 7.60
3.88
REG 8.14
4.21
BAY 8.26
2.69
KWM 9.00
2.84
NC 9.24
3.36
Table 3: Means and standard deviations of
algorithm ranks on real-world problem set.
All four ANOVA results (for ranks and scores of all and real-world problems) were significant (all F>1.75;P<0.05). All algorithms were found to perform significantly better than either baseline by at least one analysis of variance, and many by more than one. Furthermore, pairwise comparisons indicate that some pairs of algorithms were significantly different. However, the four analyses of variance did not agree on clearly delineated groups of algorithms.
Figures 1-4 show the pairwise comparisons. Each horizontal line indicates a set of algorithms which were not found to be significantly different by pairwise comparisons.
In looking at the figures, one seems justified in concluding that the leftmost methods (FS, NET, TRE, KN, and GP) performed significantly better than the rightmost (NC, REG, and KWM), but finer distinctions are not unambiguously supported.
![]()
Figure 1. Pairwise comparisons over all problems based on rank.
Accuracy decreases left-to-right. F13,481=26.33.
![]()
Figure 2. Pairwise comparisons over all problems based on
scores.
Accuracy decreases left-to-right. F13,481=23.73.
![]()
Figure 3. Pairwise comparisons over real-world problems based
on ranks.
Accuracy decreases left-to-right. F13,364=18.14.
![]()
Figure 4. Pairwise comparisons over real-world problems based
on scores.
Accuracy decreases left-to-right. F13,364=16.71.
Table 4 shows the significant correlations (all |t0.05(2),36|>2.028; P<0.05) that were detected between accuracy scores and the various properties of problems. The only algorithms not found to be affected by number of classes were MAH and NCM. No algorithm was found to be sensitive to the proportion of attributes that were nominal versus numeric (but see ANOVA results, below).
For the number of classes, the correlation with GP is significantly stronger than with any other algorithm (all Z0.05(2)>1.96; P<0.05) except NET (Z0.05(2)=1.89; P>0.05); none of the other correlations with this attribute are significantly different. However, the statistical power for most of these tests is quite low; the probability of detecting a significant difference between KNW and TRE, for example, is only 3%.
Likewise, although the significant correlations with the number of attributes were not significantly different, the power of the test between the most extreme difference (REG vs. KWM) was only 11%.
property of task
algorithm r
number of classes
GP -0.80
NET -0.57
REG -0.52
NC -0.46
KNW -0.44
TRE -0.42
KN -0.39
KWM -0.39
BAY -0.36
FS -0.33
number training cases
GP -0.46
number of test cases
GP -0.35
number of attributes
REG -0.51
MAH -0.42
KWM -0.37
Table 4: Significant correlations for accuracy scores (P<0.05).
The full
problem set was used.
Table 5 gives the mean ranks of algorithms on the eight
subsets of problems described above. Significantly different pairs
are underlined.
alg trn+ trn- tst+ tst-
2cat >cat nom num
FS 3.08 4.92 2.92
5.08 4.64 3.21 5.05 3.63
NET 4.82 4.26 5.29 3.79
4.26 4.88 3.35 4.96
TRE 5.61 3.76 4.76 4.61
4.90 4.41 2.95 5.30
KN 4.18 6.45 4.16 6.47
6.24 4.18 7.20 4.64
GP 7.18 4.50 7.05
4.63 3.76 8.41 5.60 5.93
MAH 6.76 6.87 6.63 7.00
7.36 6.15 6.20 7.04
KNW 7.50 7.16 7.32 7.34
8.19 6.26 7.20 7.38
NCM 6.68 8.26 7.71 7.24
7.79 7.09 7.70 7.39
REG 6.87 8.47 7.05 8.29
6.17 9.53 8.70 7.30
BAY 7.95 8.34 7.63 8.66
8.21 8.06 6.90 8.59
NC 9.03 9.18 9.47 8.74
8.60 9.74 10.85 8.48
KWM 10.18 8.55 10.00 8.74 10.50
7.97 9.00 9.50
Table 5: Mean ranks of algorithms on subsets of problems. trn+=large
training set, trn-=small training set,
tst+=large test set,
tst-=small test set, 2cat=two
categories, >cat=more than two categories,
nom=mostly
nominal attributes, num=mostly numeric attributes.
Significant results of ANOVA applied to the four problem dichotomies are shown in Table 6. Only six significant differences were found; however, most of the tests had fairly low power (P[Type II error]>45% in most cases), so it is quite possible that additional differences exist.
The elevated performance of GP on problems with fewer training cases may be an artifact of the experimental procedure, because some of the larger training sets caused GP to run too slowly and were therefore reduced through random sampling; this reduction may have created a disadvantage for GP on the larger training sets due to loss of vital training information. This may also explain the negative correlations involving GP and the sizes of the training and test sets reported above (Table 4).
Not surprisingly, two of the algorithms (GP and REG) performed significantly better when the task involved discriminating between only two categories rather than three or more. However, the difference is reversed for KWM; this may be spurious.
The reduced performance of TRE on problems involving more
numeric than nominal attributes may indicate that the decision tree induction
algorithm used for this study is not adequately handling continuous attributes,
and that improvements such as those described in [Quinlan 1996] might be
necessary to achieve more competetive results in this region of the problem
space.
dichotomy algorithm
ranks
F
#categories GP
two= 3.76 more=8.41 23.71
#categories KWM
two=10.50 more=7.97 9.03
#categories REG
two= 6.17 more=9.53 7.98
test cases FS
few= 5.08 many=2.92 7.43
attributes TRE
nom= 2.95 num=5.30 7.12
training cases GP
few= 4.50 many=7.18 5.56
Table 6: Significant differences between mean ranks of an algorithm
on a
partitioning of the problem set into two subsets (dichotomy).
All F shown
are significant (F1,36=5.44; P<0.05).
All algorithms exhibited a wide range of ranks on the
real-world problems. Table 7 shows the ranges of ranks of algorithms
when tied scores are assigned the best rank among the ties, rather than
averaging them. Most of the algorithms achieved top rank (rank 1)
at least once; most of them also ranked 9th at least once.
Algorithm
Range of ranks
TRE
1-7
NET
1-8
NCM
1-9
GP
1-10
FS
1-10
BAY
1-11
KN
1-11
REG
1-12
KNW
1-12
NC
1-13
MAH
2-9
KWM
2-10
--MAJ--------------2-12--
RND
6-14
Table 7: Ranges of ranks on real-world problems.
The dashed line highlights the MAJ baseline.
Table 8 gives the observed frequencies of achieving the
top rank (highest accuracy). Note that the frequencies do not sum
to 1 because of occasional ties for the top rank. Thus, although
it might seem that one could achieve top rank with at least 90% confidence
by simply employing the top three algorithms in Table 7, these would collectively
achieve top rank on only 55% of the problems.
Algorithm
Frequency
FS
35%
NET
28%
KN
28%
GP
28%
KNW
10%
NCM
7%
REG
7%
TRE
7%
--MAJ------------3%--
BAY
3%
NC
3%
Table 8: Frequency with which
an algorithm achieved top rank
on real-world problems.
The dashed line highlights the MAJ baseline.
As shown in Table 9, one would have to employ seven algorithms
to achieve top rank with 95% confidence; this table gives the probability
of achieving top rank on the real-world problem set using the given algorithm
groups.
group size P[#1]
group members
1
35%
FS
2
59%
FS GP
3
76%
FS GP NET
4
83%
FS GP NET REG
5
90%
FS GP NET REG NCM
6
93%
KN FS GP NET REG NCM
7
97%
KN KNW FS GP NET REG NCM
8
100%
KN KNW FS GP NET REG TRE NCM
Table 9: Number of algorithms required to achieve top rank with the
given frequency on
the real-world problem set. P[#1] is the frequency of achieving
top rank.
Table 10 gives the probability of achieving first or second
rank using the given group of algorithms. As can be seen from the
table, achieving first or second rank on the real-world problem set can
be assured by employing a group of only four algorithms.
group size P[#1
or #2]
group members
1
55%
NET
2
86%
FS NET
3
93%
FS GP NET
4
100%
KN GP NET TRE
Table 10: Number of algorithms required to achieve first or second
rank with the given
frequency on the real-world problem set. P[#1 or #2] is the
frequency of achieving first or
second rank.
Regarding the No Free Lunch theorems, it is clear
that one can in fact get a "free lunch" of sorts in the real world, because
the expected accuracy for any of the algorithms tested here is better than
random.
Unfortunately, none of the methods tested qualifies as a "silver bullet" algorithm which always or even almost always produces the highest accuracy scores on real-world classification problems. The algorithm most frequently ranking first (FS) did so only 35% of the time. Thus, one cannot simply keep a general learner handy and expect to always achieve the highest possible score. Two alternatives are to (a) pick an algorithm based specifically on the properties of the task at hand, or (b) maintain a "toolbox" of general learners and apply them all to each new problem, choosing the best learner a posteriori.
One could try to follow strategy (a) by looking up the problem's properties in Table 5 and picking an algorithm that is expected to have a favorable rank. However, most of the differences between corresponding pairs of properties shown in this table are not statistically significant. This could be due to lack of statistical power, but it seems likely that many of the nonsignificant differences did in fact result from sampling error, and their use for selecting an algorithm is therefore not recommended. Even if many of these differences are real, it is not possible using this data to tell which those are, so Table 5 is of little practical value in this regard.
Table 4 is also of questionable value. The negative correlation with the number of classes appears to be quite weak for FS, which has already been noted as one of the more promising algorithms. Likewise, the correlation appears to be relatively weak for TRE and KN. Although most of the differences in this table were not statistically significant, the power of the test was quite low, so it is not clear how these results should be applied in practice.
The negative correlations with the number of attributes were significantly stronger for REG, MAH, and KWM than for the remaining algorithms, but REG and KWM have already been seen to compete poorly, so again, the information is of questionable value.
Even following strategy (b) can be more difficult than it may seem, because achieving top rank with 95% confidence requires (for this problem set) a toolbox of at least seven algorithms. However, FS and NET together always ranked fourth or better, and on both the full problem set and the real-world subset, they had the best mean ranks (though they did not always rank best on individual problems). Armed with just these two methods, one can achieve first or second rank (on the real-world problems used here) with 86% probability. Extending the toolbox with GP yields first or second rank 93% of the time (again, assuming the real-world problem set used in this study). Thus, reliably achieving first or second rank does not appear to require a large suite of tools, but achieving top rank does. (Obviously, "top rank" in this context refers to performance relative only to the suite of tools examined here.)
It is difficult to recommend a single algorithm when only enough resources are available to try one method, because whereas TRE produced the highest mean accuracy in both analyses, FS produced the best mean rank and NET yields the highest probability of achieving first or second rank (55%). Given the lack of statistically significant differences between these three, selecting any one of them for a new task may be a reasonably safe choice, though one is still advised to try as many different algorithms as resources permit.
As noted above, picking an algorithm based on problem attributes such as those investigated here may not be an effective strategy, given the general lack of significant differences detected for most of the algorithms on most of the problem dichotomies. Possibly what is more imporant than generic properties such as the number of categories or the number of attributes in predicting how well an algorithm will perform on a new problem is the structure of the problem itself, and whether the inductive bias of a particular learner is in some sense consistent with the problem structure. Unfortunately, no fully general methods for predicting this consistency beforehand are yet known.
As suggested by [Wolpert and Macready 1996], if one can afford to analyze a problem and design an algorithm specifically for that task, that would seem to be ideal. According to those authors, "it is well known that generic methods (like simulated annealing and genetic algorithms) are unable to compete with carefully hand-crafted solutions for specific search problems," and one might presume that this is true of supervised learning as well.
The beauty of black-box algorithms, however, is their
ready application to arbitrary problems, with little preparation and virtually
no analysis. Indeed, one might conceive of using a standard set of
black-box algorithms to empirically measure the complexity of systems under
study [Oakley 1996]. Often these systems are so complex that deriving
useful analytical characterizations is simply not practical. As shown
by the experimental procedure followed here, it is possible to maintain
a library of general black-box algorithms which can be quickly tested on
a new problem once the training data is properly formatted. Once
these tests have been carried out, making exploratory modifications to
the standard algorithms may be a very rewarding exercise, and may be a
good starting point for a more in-depth analysis of the problem.
Some strategies for picking a single black-box algorithm based on certain generic properties of the task at hand have been considered, and have been shown to be rather unpromising. Suggestions were instead made for maintaining a library of standard algorithms to apply to each new task, possibly leading to modification and customization of the best-performing method for a particular problem. Alternatively, practitioners are encouraged to design custom algorithms specifically suited to the problem at hand, when this is feasible.
Additional problems and additional algorithms would enhance the value of this work. In particular, more problems would increase the power of the statistical tests employed, possibly revealing additional significant differences. Additional algorithms could be produced simply by constructing hybrids of existing methods; for example, applying feature selection and cross-validation to other algorithms besides K-nearest-neighbors. There are also other generic algorithms which were not tested here, such as logistic regression. It would be interesting to see if any of the inferences drawn here can be falsified by any algorithm(s) not included in this investigation.
Finally, it must be emphasized that the results presented here were all produced under rather stringent resource constraints. It is certainly conceivable that the results would be very different had the training phases and/or the exploration of the parameter spaces been significantly extended. The constraints imposed in this study were dictated by the available hardware and the amount of time available for the study. As a practical matter, these may or may not be roughly equivalent to the level of resources available to those seeking to apply these methods to real problems. Accordingly, the results obtained here will be of varying practical value for real practitioners.
Furthermore, because neural networks and the evolutionary processes modelled by genetic algorithms operate in parellel in the real world but were executed on a serial processor in this study, the results presented here should not be misconstrued as indicating bounds on the capabilities of analogous processes occurring in nature.
[Chellapilla 1997] Kumar Chellapilla, "Evolutionary Programming with Tree Mutations: Evolving Computer Programs without Crossover," in Proceedings of the Second Annual Conference on Genetic Programming, pp. 431-438, Morgan Kauffmann, 1997.
[Falconer and Mackay 1996] D. S. Falconer and Trudy F. C. Mackay, Introduction to Quantitative Genetics, Longman, 1996.
[Gathercole and Ross 1997] Chris Gathercole and Peter Ross, "Small Populations over Many Generations can beat Large Populations over Few Generations in Genetic Programming," in Proceedings of the Second Annual Conference on Genetic Programming, pp. 111-117, Morgan Kauffmann, 1997.
[Hassoun 1995] Mohamad H. Hassoun, Fundamentals of Artificial Neural Networks, MIT Press, 1995.
[Kauffman 1993] Stuart A. Kauffman, The Origins of Order, Oxford University Press, 1993.
[Koza 1992] John Koza, Genetic Programming: On the Programming of Computers by Means of Natural Selection, MIT Press, 1992.
[Koza, et al. 1997a] John R. Koza, Forrest H. Bennett III, Martin A. Keane, and David Andre, "Evolution of a Time-Optimal Fly-To Controller Circuit using Genetic Programming," in Proceedings of the Second Annual Conference on Genetic Programming, pp. 207-212, Morgan Kauffmann, 1997.
[Koza et al. 1997b] John R. Koza, Forrest Bennett III, Jason Lohn, Frank Dunlap, Martin A. Keane, and David Andre, "Use of Architecture-Altering Operations to Dynamically Adapt a Three-Way Analog Source Identification Circuit to Accommodate a New Source,"in Proceedings of the Second Annual Conference on Genetic Programming, pp. 213-221, Morgan Kauffmann, 1997.
[Langdon and Poli 1997] W. B. Langdon and R. Poli, "Fitness Causes Bloat," Technical Report CSRP-97-09, University of Birmingham, 26 March 1997.
[Luke and Spector 1997] Sean Luke and Lee Spector, "A Comparison of Crossover and Mutation in Genetic Programming," in Proceedings of the Second Annual Conference on Genetic Programming, pp. 240-248, Morgan Kauffmann, 1997.
[Manly 1994] Bryan F.J. Manly, Multivariate Statistical Methods, Chapman & Hall, 1994.
[Masters 1995] Timothy Masters, Neural, Novel & Hybrid Algorithms for Time Series Prediction, John Wiley & Sons, 1995.
[Mitchell 1997] T.M. Mitchell, Machine Learning, McGraw-Hill, 1997.
[Murphy and Aha] P. Murphy and D. Aha, UCI Repository of machine learning databases [http://www.ics.uci.edu/~mlearn/MLRepository.html]. Irvine, CA: University of California, Department of Information and Computer Science.
[Oakley 1996] E. Howard N. Oakley, "Genetic Programming, the Reflection of Chaos, and the Bootstrap: Towards a Useful Test for Chaos," in Proceedings of the First Annual Conference on Genetic Programming, pp. 175-181, MIT Press, 1996.
[Quinlan 1986] J. R. Quinlan, "Induction of Decision Trees," Machine Learning, vol. 1, pp. 81-106, 1986.
[Quinlan 1993] J. R. Quinlan, C4.5: Programs for Machine Learning, San Mateo: Morgan Kaufmann, 1993.
[Quinlan 1996] J. R. Quinlan, "Improved Use of Continuous Attributes in C4.5," Journal of Artificial Intelligence Research, vol. 4, pp. 77-90, 1996.
[Soule and Foster 1998], Terence Soule and James A. Foster, "Effects of Code Growth and Parsimony Pressure on Populations in Genetic Programming," Evolutionary Computation, vol. 6, pp. 293-310, 1998.
[Soule, et al. 1996] Terence Soule, James A. Foster, and John Dickinson, "Code Growth in Genetic Programming," in Proceedings of the First Annual Conference on Genetic Programming, pp. 215-223, MIT Press, 1996.
[Wolpert 1996] David Wolpert, "The Lack of a priori Distinctions Between Learning Algorithms," Neural Computation, vol. 8, pp. 1341-1390, 1996.
[Wolpert and Macready 1996] David H. Wolpert and William G. Macready, "No Free Lunch Theorems for Search," Santa Fe Institute Technical Report #SFI-TR-95-02-010, 1996.
[Wolpert and Macready 1997] David H. Wolpert and William G. Macready, "No Free Lunch Theorems for Optimization," IEEE Transcations on Evolutionary Computation, vol. 1, pp. 67-82, 1997.
[Zar 1996] Jerrold H. Zar, Biostatistical Analysis, Prentice Hall, 1996.
nl2:
if(x<3)
value=sin(x)+y*z-w*w;
else
value=x+sin(y+z)-w;
category=value<0 ? 0 : 1;
nl3:
if(a>b)
value=c*d-e*f;
else
value=a+b*c-d*e+f;
category=value<0 ? 0 : 1;
nl4:
value=-a+b*c-d*e+f;
category=value<0 ? 0 : 1;
nl5:
value=sin(a)-cos(b)+tan(c)-d+e;
category=value<0 ? 0 : 1;
nl6:
value=a/b-c*c+4*d/e+3*a;
category=value<0 ? 0 : 1;