Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany
Der thermische Wirkungsgrad htherm ist bei isothermem Wärmeübergang (TE in den H- und TC in den K-Zylindern sind konstant) und bei 100% Wärmeaustausch im Regenerator gleich dem Carnot-Wirkungsgrad hthermC = (TE - TC)/TE. Dieser ideale thermische Wirkungsgrad wird natürlich in der realen Maschine nicht erreicht. Der Wärmeübergang ist zwar gut, aber eben nicht isotherm; die Temperaturen TE und TC sind nur annähernd konstant. Die Grädigkeit des Wärmeübergangs läßt sich für einen sehr langsam verlaufenden Energieaustausch aus den Wärmekapazitäten der Beregnungsflüssigkeitstropfen (bzw. aus der Wärmekapazität der Metallspäne) und der Wärmekapazität des Gases errechnen. Siehe Kapitel 15. Dies ist experimentell bestätigt worden. Bei der Wärmeübertragung auf das Gas spielen die Gasgeschwindigkeit an der Wärmeübertragungsfläche, Abstand und Masse der Beregnungströpfchen, die Wärmeleitfähigkeit des Gases, sowie letztlich auch der Wirkungsgrad des Regenerators eine Rolle. Reibungsverluste in der Gas- und Flüssigkeitsströmung sind wegen der geringen Drehzahl ebenfalls gering; dennoch, diese, sowie die Verluste im Regenerator, verringern den Wirkungsgrad. Siehe auch das eingangs in Kapitel 1 Gesagte zur Definition der Betriebszustände für das Computerprogramm.
Neben dem thermischen Wirkungsgrad ist der Ausnutzungsgrad "n" eine wichtige Kenngröße. "n" ist das Verhältnis der Nutzarbeit dieser Maschine "W" zu der Nutzarbeit des idealen Stirlingprozesses " Wi " mit dem Regeneratorvolumen VR = 0 im gleichen Arbeitsraum zwischen Vmax und Vmin .
(4.1)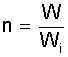
Für das Zylinderpaar H1-K1 -bei konstanten Temperaturen TE und TC- entspricht die Arbeit "W" der Fläche, die durch die Kurve im P-V (Abb.3) oder im T-S Diagramm (Abb.6) gebildet wird. Üblicherweise wird "W" aus dem gemessenen P-V Diagramm, dem Indikator Diagramm, ermittelt. Die ideale Stirling-Nutzarbeit " Wi " entspricht der Fläche in den Diagrammen, die durch die Isothermen TE und TC sowie durch die Isochoren bei Vmax und Vmin gebildet wird. (Fläche (I) - (II) - (III) - (IV) - (I) siehe das P-V Diagramm -Abb.3- und siehe auch den "Rahmen" im T-S Diagramm Abb.6). Im idealen Stirling Prozeß erfolgen die 4 Zustandsänderungen zeitlich nacheinander. Hier wird während der Abwärtsbewegung des Arbeitskolbens nur "positive" Arbeit verrichtet, also Expansionsarbeit, während bei der Aufwärtsbewegung des Arbeitskolbens das Gas stetig verdichtet wird; in dieser Phase wird also Kompressionsarbeit benötigt. Dies ist nur bei diskontinuierlicher Bewegung eines Verdrängerkolbens möglich, bzw. bei diskontinuierlicher Bewegung beider Kolben in einer idealen 2-Zylinder 2-Kolben Maschine. Siehe dazu im Gegensatz -Abb.3a- den Verlauf der Arbeit im Expansions- und Kompressionszylinder in der realen Maschine mit kontinuierlich phasenversetzter sinusförmiger Bewegung der beiden Arbeitskolben. Hier werden die sich zeitlich überlappenden Zustandsänderungen deutlich.
So ergibt sich Wi als die Nutzarbeit des idealen Stirling Prozesses als Summe von Expansionsarbeit bei der Temperatur TE und Kompressionsarbeit bei der Temperatur TC. Ersetzt man entsprechend Gl.(2.17) P nach dem idealen Gasgesetz durch: P = MG * RG * TE / VG , so erhält man für das Differential der Expansionsarbeit im idealen Stirling Prozeß:
(4.2)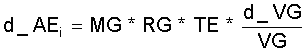
Hierbei ist zu beachten, daß die ideale Stirlingmaschine nur einen Gasraum haben kann -hier mit dem Volumen VG-, in dem die 4 Zusttandsänderungen zeitlich nacheinander ablaufen. Durch Integration des Differentials d_AEi von Vmin bis V max ergibt sich die Expansionsarbeit "AE" pro Umdrehung als Ausdehnungsarbeit während der isothermen Zustandsänderung bei TE:
(4.3)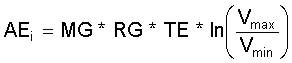
Analoges gilt für die Kompressionsarbeit "AC" von Vmax bis Vmin bei der Temperatur TC im idealen Stirling Prozeß:
(4.4)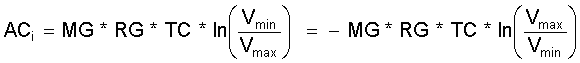
Die Nutzarbeit des idealen Stirlingprozesses ergibt: Wi = AEi + ACi :
(4.5)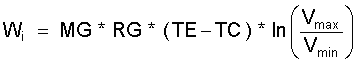
oder mit (P0 * V0)/T0 = MG * RG :
(4.6)
Da im idealen Prozeß der Regenerator intern die isochore Energiezufuhr bei Vmin mit dem isochoren Energieentzug bei Vmax ausgleicht, ist von außen keine weitere Energiezufuhr oder Kühlung erforderlich als die, die für die isotherme Expansion und für die isotherme Kompression benötigt wird. Die Nutzarbeit "Wi" des idealen Stirlingprozesses ist nach obiger Gleichung Gl.(4.5) oder Gl.(4.6) bestimmt durch die Temperaturen TE und TC sowie durch das erreichbare Volumenverhältnis Vmax / Vmin und ist direkt proportional der Gasmasse in den Zylindern, und damit auch bestimmt durch das Ruhevolumen V0 und den Ruhedruck P0. Grundsätzlich gilt dies auch für die Nutzarbeit "W" in der realen Maschine. Das Volumenverhältnis Vmax / Vmin wird durch Regelungsvolumen (siehe Gl.(2.6) und Gl.(2.7) ), Regeneratorvolumen "VR", sonstiges "Totvolumen", den Versatzwinkel δ und durch die geometrischen Verhältnisse der Kurbeltriebbewegung, die ja den idealen Bewegungsablauf nur annähern kann, bestimmt. Vmax / Vmin und damit "W" und der Ausnutzungsgrad "n" werden geringer mit steigendem "VR", bzw. mit steigendem "Totvolumen". Ebenfalls verringert sich Vmax / Vmin , wenn statt des rein sinus-förmigen Bewegungsablaufs der Kolben durch die Kurbelschleifentriebe, wie sonst üblich Pleuelstangen Kurbeltriebe verwendet werden. Anstelle von VE und VC nach Gleichungen Gl.(2.6a) und Gl.(2.7a) sind für einen Pleuelstangen Kurbeltrieb die Gleichungen Gl.(2.6b) und Gl.(2.7b) anzuwenden. Aus einem Pleuelstangen Kurbeltrieb resultiert ein geringeres Volumenverhältnis Vmax / Vmin bzw. jeweils größere Werte für Vmax und Vmin .
Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen