Numerical Solution to the Schrodinger's Equation
One dimensional Schrodinger Equation. This is one of the most familiar quantum physic equation. It is considered as trouble to solve this equation. I will explain how I solved this equation in this page by defining the problem and making it clear what exactly, someone need to do. I made that work around 1998 and I still get emails from people asking for the "Source Code." It became 2002 now. I am not going to give the source code out, but I want to tell some about solving the equation. If you have any questions, e-mail me I will try to help you. You can also search 'Numerov's Method' on the web to find out more information. But I recomend you to read this web page.
And you may also consider to read
the paper
"Computational Solutions to the Schrodinger Equation", P.C.CHOW, AJP Vol 40, pp
730-734, 1972
This excelent paper uses 'Numerov's Method' to solve the wave functions
numerically. But sometimes it felt like you are left out to your
own imagination, somehow. After you read what I wrote in this web
page, that paper will make much more sense to you.
After solving Schrodinger's equation, you can
confirm your own result with comparing to the results in the figure that
published in our journal paper,
C.Besikci, A.T. Bakir and B.
Tanatar, "Dielectric Screening Effects on Electron Transport in
GaInP/InGaAs/GaAs Quantum Wells," Journal of Applied Physics, vol. 88, pp.
1504-1511, 2000.
Some Notes on Solving Schrodinger's Equation
![]()
Let us define the problem: I will make that definition as simple as possible so that anyone can understand the thing we want to do.
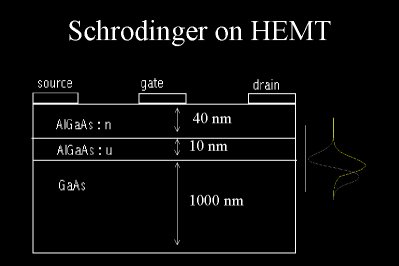
For example, we have an InGaAs/GaAs Quantum well. Which the conduction band is abruptly broken and sperated by a constant energy level due to differences in material properties (dopings, etc) to set up a phonemea which we call quantum well. The bottom of that well goes down to energy levels around few meVs, where electrons which have low energies are traped in two dimensional subbands. Now consider an free electron moving in 3D in InGaAs on conduction band. The question comes at the point where a free 3D electron goes into a 2D quantum well, (by electrical field force or by a photon hit on it or by anohter scattering event, etc). Where this electron will be? Say it is on the first 2D subband, then we know the total of 2D subband bottom energy (which is 'always' called as static energy) and kinetic energy of the electron will give us the total energy of that electron which that electron brought to there from the 3D system. Well, we accepted that our electron is in the 1st subband, now we want to find out how far away it could be from the point where quantum well is formed, the point or the border between two semiconductor material. Square of the wave function gives us the probability of being somewhere in quantum well. So we can say something like that, it is 70% possible that our electron is 10 nm away from the quantum well (DeltaEc) junction into GaAs. Or we can say, it is 10% possible that our electron is 50nm away from the point it entered into quantum well.
So when we solve that equation, we will get the subband energy levels (1, 2, 3, 4, 5, .....). Subbands will have energy levels lower than the first 3D conduction band. If the you find an energy level higher than the energy level of the first 3D (gamma) conduction band of GaAs, that means you are making a mistake. (Just a note, we have 3 3D conduction bands in GaAs).
The major problem about solving Schrodinger's equation is that we have only one equation but two unknowns for each subband quantization level. Those unknowns are quatized subband energy levels (Em) and appropriate Wave functions Y(z) for a subband.
What we know about Em and Y(z) are: Em is constant for a given material. Say it is around 43 E-3 eV for the first subband in a GaAs at 300K. Y(z) 's amplitude depends on the distance from the point that an electron enters into quantum well. (say -20 nm to 100 nm, where -20nm refers to Y(0)).
The solution is trial.
We will choose the subband energy level as say 0 eV, and will try to find out the wave function accordingly. if the wave function that we found does not satisfied the conditions to validate, then we will chose another subband energy and try over again to find the wave energy. we can say chose these new subband energy level with a resolution of 0.001 eV..
Now, how we know the wave function we have for the choosen subband energy is correct? So if we know it is the right wave function, we will know that we have the right solution to the equation and the subband energy we choosed is the right energy level for that subband.
To find the wave function, we will devide the wave function into two parts at the point where quantum well abrupt junction occures. we will call this point as default 'turning point'. But the real 'turning point' is the first point where the square of the wave function changes it's sign. (say from possitive to negative, or negative to possitive for the first time). If we cannot find a 'real turning point' we may consider to use the default turning point. Well, that 'square of the wave function' it is found from =a_constant*(V(z)-Em), since we know V(z) is the potantial energy, which could be found by solving Poisson's equation, Em is the subband energy.
Now we have two wave functions artifically separated at that 'turning point'. since this is a continues function, the slope of these two functions should be the same at the turning point. Math says, 'the slope of a function' is the first derivative of that function. Then we are required to find the derivative of these two functions and check if they match at that turning point.
Ok, then we know how we will validate the wave function, but where is the wave function?
Numerov's Method comes to our help at that point. It is a method to solve the equations that have second order derivative parts in it. You may set the boundary conditions according to the Chow's paper or to the values that you might find reasonable according to the constants you use in the calculations. I have choosen 0 and 1 as initial border values for the appropriate places. Chow's paper gives us the derivative in form of Numerov's equation to solve the inner and outer ingegrals. In the paper there is radial part of the schrodinger's equation. You can simply ignore it, if it is going to be 'zero' all the time within your case. I had no radial parts to include, so I ignored it.
By simply solving the wave function from 'turning point' to left, we will find the left part of the wave function. and by solving from the 'turning point' to right, we will find the right part of the equation. No we have two parts of the equation, so we can check if these two parts satisfy our rule of same slopes (matching the first derivatives).
If everything is Ok, then we have the solution of a 'hard to solve' equation. And it becames easy to solve, once you did that work.
Some results from my preliminary works are shown beneath
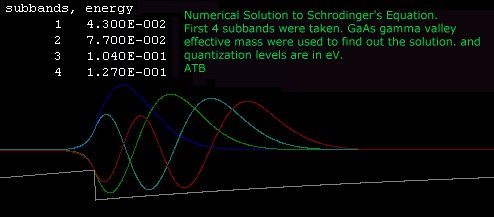
While the square of the wave function gives us electron occupancy. We can use schrodinger for device simulations. That is why I needed Schrodinger solution. Here is two examples where we can use Wave Function to simulate devices.
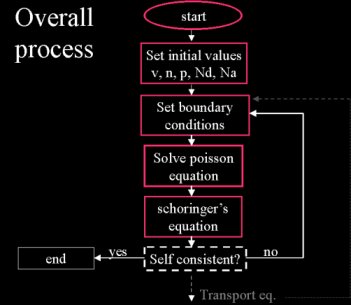
Self Consistent
Solution of Schrodinger's Equation Coupled with Poisson's
Equation:
And MODFET 2Deg
Quantum Well Solutions