The Sun as a
Pulsar
The sun has been found to oscillate with a period of 2 hours, 40 minutes, or 160 minutes. We are now going to ask an interesting question. Does the sun’s gravitational force oscillate as well?
For an answer to this intriguing question we turn to some recent ongoing studies of the earth’s gravitational field and the tidal effects of the sun and moon. In 1992 a newly developed Superconducting Gravimeter was activated in Potsdam, Germany. This device, intended to provide the most accurate long-term measurements of the forces of gravity at one place, has been taking highly accurate measurements of the earth’s gravity once a minute since it was put in place. These measurements provide a baseline from which we may observe the gravitational effects of the sun.
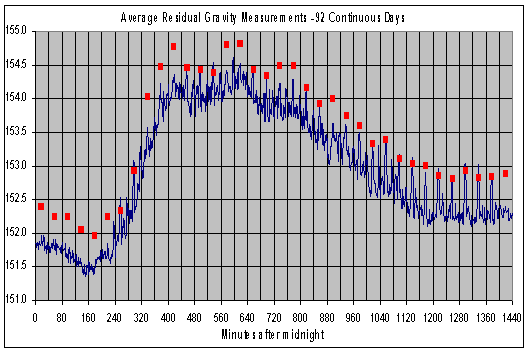
Data are available from the Internet for the six-month period of July 1, 1992 through December 31, 1992.[1] This data consists of readings, taken every minute, of the absolute gravity measurement, and a residual measurement which is the absolute measurement corrected for the known tidal effects of the sun and moon. The above figure is a plot of the daily average residual over the period of October 1992 through December 1992. Note that each point is the average of 92 days of residual readings at exactly the same time of day. The square markers on the chart are exactly 40 minutes apart, and correspond almost exactly with a peak in every 40-minute time period. In other words, this chart shows an unmistakable pulsing of the residual gravitational reading of the superconducting gravimeter at exactly once every 40 minutes, or four times more often than the 160-minute period we were seeking from the sun’s known pulsation.
To illustrate the effect even more distinctly, the data from this three-month period was divided into blocks of 160 minutes, starting at midnight. To eliminate the trend which is apparent in the residual measurements, the residuals for each 160 minute period were normalized to the average residual for the period. The figure below provides the result of averaging each 160-minute block over the three-month period. Each point is an average of 827 measurements, taken at exactly the same time within the 160-minute period. The 40-minute cycle for the residual measurements is indisputable! (Several smaller cycles appear to be present as well, but we shall not consider these here, except to note that similar side lobes appear in the light curves of many pulsars.)
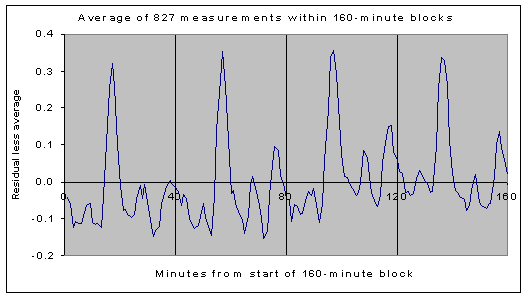
Analysis of blocks of 160 minutes. Each point is an average of 827 residual measurements, taken 160 minutes apart, for three months. Potsdam Superconducting Gravimeter.[2]
An interesting anecdote will, I hope, make clear how well defined this cycle is, and why the analysis considers only three months of data. During my studies I compared results of this test on a month-to-month basis over the six months of data available. And while each month’s chart was virtually identical to the first figure above, the peaks of the first three months were displaced from the peaks of the second three months by exactly 20 minutes. This was very puzzling!
Reviewing the data a day at a time, the
discrepancy was finally isolated to a single day—September 30. The peaks on September 30 and earlier were
displaced 20 minutes from the peaks on October 1 and later. After pondering
such a puzzle for several weeks it suddenly occurred to me that such a displacement
would occur if there had been a change of one hour in the test baseline time
(60 minutes – 40 minute period = 20 minute shift). And such an hour shift could occur if there were a change from
daylight savings time to standard time on that day. But the observed change occurred on September 30, while in the
United States the change from daylight savings time to standard time takes
place in late October.
A
search of the Internet turned up the answer.
Indeed, in Germany where the tests were being conducted, the change from
daylight savings time takes place September 30 at midnight. Clearly, someone
had changed the master clock for these experiments from daylight savings time
to standard time. Imagine being able to determine the date of changing from daylight
savings time in Germany from pulsations in gravitational measurements.[3] This is very convincing evidence that the
pulses are real.
Of course, changing the master clock for a multi-year project is poor judgement.
Interpreting the gravity pulses
There are several reasons to believe that the pulses are caused by the sun. In the first place, we were looking for just such an effect based on the sun’s known 160-minute oscillation. The second reason is that the pulses are very sharp and short-lived, and unlike a slow oscillation that would be expected if the earth were to resonate at this frequency.
At
first it is tempting to think that the super-sensitive gravimeter is detecting
some rapid change in the gravitational attraction of the sun (at least that is
my mindset). However, the sun’s
gravitational force at this distance is so weak that its effect on any small
object such as the gravimeter sensor would be negligible. Furthermore, if it were the sun’s
gravitational force that were being measured, there would be a difference in
effect during the day, when the sun is overhead, and at night, when the sun’s
forces add to the earth’s gravitational attraction. But no such effect is apparent.
Instead, all peaks are toward greater attraction to the earth. It is as if the oscillation of the sun
causes a change in the earth’s gravitational field.
My explanation is as follows: The core of the sun is, of course, extremely hot, but not always hot enough to create significant fusion processes. Those that do occur, however, gradually increase the heat within the core until at some point significant sustaining fusion reactions take place. At this time enormous amounts of free atomic nuclei exist, and the sun’s core becomes super-gravitational. In its super-gravitational state a large number of gravitons are emitted (as well as neutrinos[4]).
However, this super-gravitational state is unstable, and the core collapses due to gravitational forces until the fusion process stops and the core cools slightly. The collapse does not have to be total, or even physically large—just enough to slow or stop the fusion process and begin the cycle again. The whole process could take just a few seconds, and would not create a major impact on the sun as a whole, although it probably is the source of the observed 160-minute oscillation.
When
the burst of excess gravitons emitted by the sun during its brief
super-gravitational state reach the earth, they trigger the earth’s matter to
emit a corresponding burst of gravitons, and the earth’s gravitational field
briefly becomes stronger than normal. It is this brief increase in the earth’s
gravitational field (about 0.3 percent), caused by responding to a brief
intense burst of gravitons from the sun, that is measured by the gravimeter and
shown in the figures above.
A new phenomenon
This observation of the 40-minute
pulses in the residual gravitational measurements of the Potsdam
Superconducting Gravimeter (SG) has led us to several conclusions. First, they are real, and show up indisputably
in the data. Secondly, they are most probably caused by the oscillation of the
sun. And third, they are centered on
the earth. This leads then to the
conclusion that changes in the gravitational field of the sun lead to changes
in the gravitational field of the earth.
It then follows that, for all objects, the gravitational force of an
object depends in part on the strength of the gravitational field in which it
resides.
I
will leave it to others to integrate this conclusion with observations
currently ascribed to the general theory of relativity.
Nothing
new under the sun!
When
I wrote the previous paragraphs I thought I was on to something completely new. Only recently, while continuing my
research on the internet, did I discover that scientists at Harvard have known about this for almost 50 years! Imagine that—knowledge that gravity does not
follow the accepted physical laws being suppressed or ignored by one of our
leading scientific institutions for half a century because they don’t know why
it happens. It’s no wonder I do my own scientific research! At least I try not
to ignore things just because I don’t understand them.
Actually it began with a French
scientist named Maurice Allais, who later received a Nobel Prize for economics.
In 1954 he was conducting a very detailed long-term experiment on the motion of
a Foucault pendulum, trying to establish a relationship between gravity and
magnetism. On June 30, 1954, a solar eclipse occurred as he was conducting his
experiment. To his great surprise he observed a significant deviation in the
swing of his pendulum during the eclipse, which disappeared after the eclipse
was over, as if the presence of the moon in front of the sun had changed the
earth’s gravitational field. He repeated this experiment during an eclipse in
1959 with similar results. Note that the effect was several million times
greater than could be attributed to the gravitational forces of the sun and
moon.
Since Allais’s amazing discovery,
similar experiments have been conducted during numerous other eclipses, mostly
with positive results.[5] The following figure
is an illustration of a
gravimeter experiment conducted during an eclipse in 1995, showing very clearly
the anomaly which occurred during the eclipse.
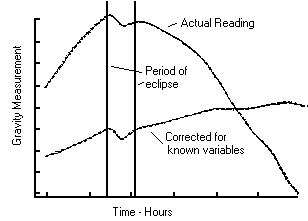
Effect of a 1995 eclipse on gravity measurements. The dip in measurements seen during the eclipse indicates an increase in the earth’s gravitational force of about 5%. (From Current Science, 72(11) 1997(783).
The evidence now in appears to show that an eclipse increases the gravitational field by up to 5% while the sun is behind the moon, but has no effect outside the path of the eclipse. There is also clear evidence that there is a 24 or 25 day periodicity in the earth’s gravitational field, presumably related to the rotation of the sun, but possibly related to the moon as well. Other experiments also seem to show that the earth’s gravitational field differs slightly when the moon is on the side away from the sun from that when the moon is on the solar side of the earth.
This remarkable phenomenon, now
established almost without doubt, is completely unexplainable within either
Newton’s or Einstein’s gravitation theories. It is a major mystery, which is
perhaps one of the reasons it has received little attention. Scientists have a
way of pushing nasty little things they don’t understand into the closet where
they forlornly hope they will go away. But this problem won’t.
Such a puzzle concerning gravity, as
you can imagine, is grist for my mill. So pardon me while I do a little
speculation on the cause.
The fact that gravity increases only
when the moon is directly in line with the sun during an eclipse suggests to me
the following. When the moon is not present, something coming from the sun
(particles?) adds a small amount to the earth’s gravitational force, as the
gravimeter experiments discussed earlier in this chapter suggest. Then when the
moon is between us and the sun, that same something alters the moon’s
gravitational field, which in turn causes the moon to radiate even more of
these ‘particles’, causing the increase in gravity which has been measured.
Thus
both the moon and earth are radiating something in response to something coming
from the sun. What is that something?
Perhaps neutrinos, or gravitons, or some other particle as yet unknown. But the
idea that it is a particle fits very nicely with observations.
This suggests to me that there may be two different kinds of gravity—the normal mass-related gravity
we take for granted, and a second form resulting from the ionized interior of
the sun or stars. In other words, the
excess gravity theorized for free nuclei may be an entirely different form of
gravity, with unique properties. The apparent gravitational force of the
sun would then consist of the addition to a mass-related gravity and the
gravitational force created within the super-hot core.
Playing with new definitions of
gravity may seem a real stretch of science, but remember that what has been
observed during eclipses cannot be explained with the old ideas of gravity, so
it is perfectly legitimate to create new ideas and concepts.
Conclusions
The sun is pulsating at a rate of once every 40 minutes,
exactly like a pulsar, and this pulsation is observed in measurements of
gravity here on earth.
The gravitational force of an object depends in part on the
strength of the gravitational force within which it resides.
Return
to the Main Page
Contact Me
Note: My original internet data source is no longer valid. If you wish to obtain the data to validate my studies, search the internet for "potsdam gravimeter gfz" or similar. If you can't find what you are looking for, contact me and I will e-mail the original data files (relatively large).
[1] Data taken originally from URL http://www.gfz-potsdam.de/pbl/pg3/ggp/sgdata.html (no longer available)
[2] The data available has been sanitized by eliminating values which fall outside that which was expected. It is possible that the actual data might tell an even more significant story.
[3] It is very surprising that the baseline time should be changed on a multi-year, continuous measurement study such as this. But the data proves it.