Shedding Light on the Solar System
This page is a little different than the other pages on this web site in that it addresses observations within the solar system, instead of in the distant universe. But these are observations for which there has never been an explanation. This page presents what I believe are some novel concepts about some of the puzzling mysteries of our solar system. Read this page with an open mind and a light spirit, and maybe it will give you a warm and fuzzy about some of the deepest puzzles of solar system astronomy.
Einstein’s Explanation for the Orbit of Mercury
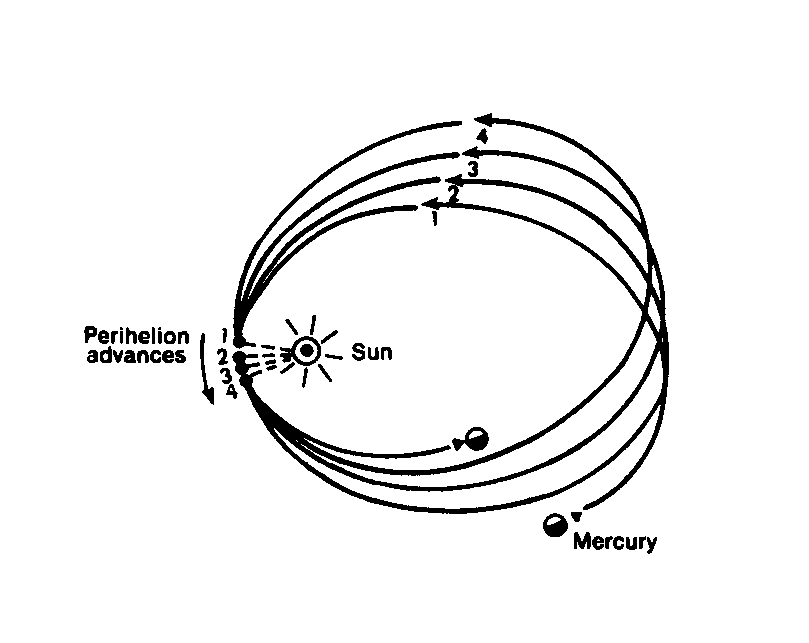
One of Einstein’s earliest successes with his General Theory of Relativity was an explanation for the advance in the perihelion of the planet Mercury. After very carefully adjusting for all known perturbations to the orbit of Mercury using Newton’s laws of gravity, astronomers had puzzled over a very small but measurable advance in the perihelion of the planet Mercury which could not be explained. They even hypothesized the existence of a planet between Mercury and the Sun to explain the effect. This hypothetical planet was named Vulcan, and of course it was never found.
The amount of deviation of the perihelion of Mercury was quite small - a mere 43 arc-seconds per century, yet all efforts to determine its cause were fruitless. The figure below illustrates the effects observed.
Einstein showed that by adding a small relativistic correction to the motion of Mercury, calculated from his general theory of relativity, the advance in the perihelion could be explained very accurately. Einstein himself made the following observation regarding the computations:
"These facts must, in my opinion, be taken as a convincing proof of the correctness of the theory."
Einstein’s correction was a very small reduction in the transverse velocity of Mercury (velocity along its path) caused by the effect of the sun’s gravitational field. I call this effect gravity drag, since it is exactly the equivalent to a drag on an object moving through a gravitational force field, and affects every object passing through a gravitational field. The figure below illustrates the gravity drag effect.
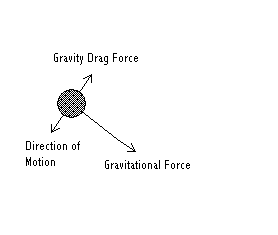
Gravity Drag in the Solar System
Gravity drag influences every object passing through a gravitational field. The magnitude of the ‘drag’, or negative force vector, is a function of the strength of
the gravitational field, and the mass and velocity of the object passing through it. That is, the stronger the gravitational field, the more mass or more velocity an object has as it passes through the field, the greater is the force tending to oppose its motion.
It has always been a puzzle to astronomers why most of the planets and moons within the solar system have nearly circular orbits (low eccentricity). If they were objects captured from outer space by the sun’s gravitational force, or if they were formed from material ejected from the surface of the sun, the most likely orbit would be a highly elliptical one such as seen with most comets. Conventional wisdom has it that these orbits would remain essentially unchanged for the object’s lifetime, except for perturbations caused by close encounters with other objects. Yet the orbits of most planets and moons within the solar system have quite low eccentricity (nearly circular). What causes low eccentricity when high eccentricity is to be expected?
Enter gravity drag. This is the mechanism by which high-eccentricity orbits could gradually (over billions of years) lose their eccentricity—that is, to change their orbits from very elliptical to nearly circular, with the sun at the center.
In a highly elliptical orbit, an object passes quite close to the sun’s surface during perihelion. At this time in the orbit two of the factors which influence gravity drag—velocity and gravitational force—are at their greatest. As a result, the planet would experience the maximum gravity drag effect. It would tend to slow slightly as it passed near the sun. As it returned to outer space, its orbit would be slightly less eccentric, causing it to reach a little less distance on the return to aphelion (the furthest point of its orbit from the center of gravity). With each orbit, the planet’s orbital path would become just a tiny bit more circular. Over millions or billions of years the orbit would eventually reach its equilibrium with gravity drag—a perfectly circular orbit (less the effects of perturbations of nearby planets and/or moons). Thus the oldest planets, those which have been orbit around the sun the longest, would have the most circular orbits, while those with more elliptical orbits would be relatively younger (i.e. acquired by the sun more recently). In a similar but more complicated way, orbits which are originally at a large angle relative to the sun’s equator will gradually shift until they are nearly perpendicular to the rotational pole of the sun, as it is for Earth, Mars, Venus and Mercury. That is, the equilibrium orbit caused by gravity drag is circular, and around the equator of the sun or gravitational object. All objects, if they are in orbit long enough, will have such an orbit, barring significant perturbations from other nearby objects.
Research in a similar vein won astronomers Joseph Taylor and Russell Hulse of Princeton University the Nobel Prize in 1993 for using a radio telescope to find two neutron stars orbiting each other. One of these stars is a pulsar—emitting regular pulses of electromagnetic energy. What is prize-worthy about this pair of stars, orbiting each other once each 8 hours, is that they have been discovered to be spiraling together at precisely the rate predicted by Einstein’s theory of relativity (2.7 parts in a billion per year). In other words, they are doing exactly what I have been suggested happened to the earth, moon and other planets—doing the gravity drag!
There is a possibility that the gravitational attraction of the sun might have been much higher in the past than we now observe it to be. If this were so, then the gravity drag effect could have been much higher in the past, causing the planets to move into nearly circular orbits much faster than with the gravitational forces present today. We might even speculate that the earth had super-gravity at one time, to explain the orbit of the moon, but then that’s carrying speculation as far as I care to go.
So we see that the gravity drag effect from Einstein’s general theory of relativity, which explains Mercury’s perihelion advance, can also provide an explanation to the observed orbits of our planetary neighbors. But there are more mysteries which can be solved by gravity drag.
One of the more puzzling aspects of planetary and lunar astronomy is why many objects orbit with one side always facing the source of gravity. Mercury, for example, rotates just three times for every two revolutions around the sun, presenting the same view toward the Sun for much of its orbit, and a very hot place it must be. The moon, of course, orbits the Earth with always the same side facing us. Put in slightly more technical terms, its rotation and revolution are synchronized. That is, the moon is rotating, but at the same rate that it revolves around the earth.
But it is not just here in the solar system that this synchronization occurs. This is also a prominent feature in close spectroscopic binary star systems, where the rotational rate of each star can be accurately measured. One must surely wonder why such an effect should occur.
Again enter gravity drag, but with a little more sophistication and complexity. Imagine a planet orbiting the sun. For simplicity we assume an essentially circular orbit. Suppose further that the orbiting planet is rotating. For the moment we will take the case shown below. This figure illustrates a point on the surface of the planet closest to the Sun (the inner rim), and another point on the outer rim on the opposite side of the planet. Each point is subjected to the gravity drag effect, but in slightly different ways. Remembering that the strength of the gravity drag depends on the strength of the gravitational field and the velocity through this field, it is apparent that velocity of motion of the point on the inner rim is slightly lower than that of the outer rim. This is because the rotational velocity of the planet is subtracted from the orbital velocity, while the rotational velocity of a point on the outer rim is added to the object’s orbital velocity. Put hopefully in a simpler manner the velocity of the inner and outer rim relative to the gravitational field are different. On the other hand, the gravitational force on the outer rim is lower than that of the inner rim because of its greater distance from the gravitational force.
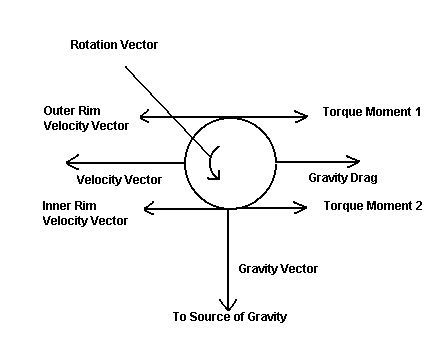
The forces at work on an object passing through a gravitational field. The general velocity vector of the object creates a gravity drag in the opposite direction, causing a very gradual decrease in velocity and causes the orbit to become slightly more circular. Because of the rotation of the object the outer rim velocity relative to the source of gravity differs from the inner rim velocity. However, the outer rim is in a slightly lower gravitational potential than the inner rim. The net effect is a small torque moment on the object, tending to increase or decrease its rotation rate until equilibrium of torque moments is reached. That equilibrium occurs when the rate of rotation equals the orbital period, as is the case with our moon.
That’s quite a lot to swallow, but the bottom line is simple. The forces created by gravity drag on the inner and outer rims are different. The net effect is that there is a torque moment on the rotating planet. The effect of this torque moment is that there will be a torque force on the planet to either increase or decrease its rotation until all torque moments due to the gravitational field equalize. And that equilibrium occurs when the rotation rate of the planet (or moon) just matches its orbital ‘year’. It does not matter which direction the initial rotation occurs, or even if there is any initial rotation at all. The torque forces will work to speed up or slow down any present rotation until equilibrium is reached. Thus the gravity drag effect explains why we always see only one side of the moon and the gradual slowing of the Earth’s rotation. Of course these torque moments are very small, and act not only to speed up or slow down the rotation until equilibrium is reached, but also to change the ‘tilt’ until the spin axis is perpendicular to the rotational plane of the gravitational force.
One indication that the earth’s rotation is slowing, for instance, is that many modern corals show well-defined growth bands that contain 365 fine bands between them, one per day. Corals of 370 million years ago show this same characteristic, but contain 400 fine daily bands. This suggests that a year at that time was 400 days long. Mounting evidence indicates that a day during the primal earth stage, 4.6 billion years ago, was only 4 ½ hours long! Clearly the earth’s rotation rate is slowing, as we would expect from the gravity drag effect.
So now that we’ve solved all the mysteries of the solar system using gravity drag, it would be great to report that the moon is slowly approaching the Earth, as would be expected from gravity drag. Unfortunately, this is not so. Laser experiments to measure the Earth/Moon distance, using laser reflectors left on the moon by several Apollo landings, indicate that the moon is receding from Earth about 3.86 cm/year. Rather than throw out all the elegant explanations for gravity drag’s effects in the solar system (the only explanations every put forth!), we will just have to speculate that other forces may also be at work with the Moon, such as changes in the Earth’s orbit due to gravity drag, interrelationships between the Sun, Earth and Moon’s gravity fields, the gradual slowing of the earth’s revolution, and maybe even the Shapiro effect. We do know that the moon has not always been receding from Earth. Tracing backward in time at the present rate of recession would place the Moon quite close to the Earth a billion years ago. Such a proximity would have created enormous ocean tides which would have swept over the Earth’s surface, causing massive erosion and other very noticeable effects. There is ample geological evidence that such an effect surely did not occur, so this recession of the Moon from Earth is fairly recent and not a long-term effect. Thus there is no conflict that the gravity drag effect is still there, working on the Moon and every other solar object as it has for billions of years.
Return to the Main Page Contact Me