Midlevel Control of Stepping Motors

• Introduction

• Hardware Solutions
• - Practical Examples

• Software Solutions
• - Simple Practical Examples
• - An Object Oriented Design
• - When Objects Won't Do

Introduction

All of the low-level motor control interfaces described in the previous sections are quite similar, at an abstract level. Each interface has some number of logic inputs. Some of these inputs may be used to directly control which switches are open or closed, others may be encoded, while others may control subsystems such as the analog to digital converter in a microstepping interface.

The states of each of these logic inputs is referred to as the control vector for the motor, and a sequence of states used to rotate the motor is referred to as a control trajectory for the motor.

For example, the control vector for controlling a permanent magnet or hybrid stepping motor using any of the control circuits shown in Figures 3.4, 3.5, 3.13, 3.14, 3.15, 4.7, 4.8, 4.10, 4.11 or 4.12 will contain 4 bits, 2 bits to control each motor winding. In each case, the control vector can be expressed as <X₁Y₁X₂Y₂>, where X₁ and Y₁ control the current through motor winding 1 and X₂ and Y₂ control the current through motor winding 2. For any interface with this control vector, the following trajectory will step the motor through one full electrical cycle, using full stepping:

1010

1001

0101

0110

1010

1010
1000
1001
0001
0101
0100
0110
0010
1010

10001000

10001010

10101010

10101000

10001000

10001000
10000000
10001010
00001010
10101010
10100000
10101000
00001000
10001000

The control vectors required for microstepped motors are more complex, but the basic idea remains the same. The problem we face here is to develop higher level control systems that will generate appropriate control trajectories, moving the motor one step, half-step or microstep each time the higher level control system requires a move.

Hardware Solutions

Early solutions to the problem of generating appropriate control trajectories for stepping motors were almost always based on direct synthesis of the control trajectory in hardware. Such solutions are still appropriate for some applications, but these days, when programmable interface controller chips are commonly used to replace random low-speed logic and when most stepping motor applications are ultimately controlled by computer systems of one kind or another, it is common to use software to generate the control trajectory.

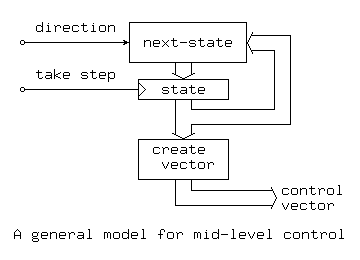
All hardware solutions to generating the control trajectory are subsumed by the general model illustrated in Figure y.1:

Figure y.1 

It is worth noting that some stepping motor control systems include addtional inputs to the mid-level control system. Common additions include half-step and brake inputs. Braking control is meaningless in full-step mode but it is of some use in half-step mode. In the latter mode, shorting unused motor windings at low speed is an excellent way to limit resonance while at higher speeds, unused motor windings should be left open for efficiency. Finally, some motor control systems include a disengage input that removes power from all windings; in this case, if brake is asserted, it typically shorts all motor windings.

Practical Examples

Amature astronomers frequently need very slow motors to turn their telescopes, and in recent years, stepping motors have taken the place of synchronous motors and gear trains for many applications, particularly for barn-door or Scotch mounts, a class of extremely simple camera mounts used in astrophotography. For this application, circuits as simple as that shown in Figure y.2 are common:

Figure y.2 

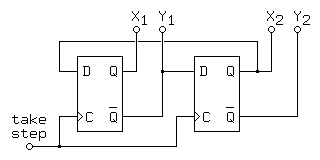
Modifying this circuit for bidirectional operation is straightforward, as is illustrated in Figure y.3:

Figure y.3 

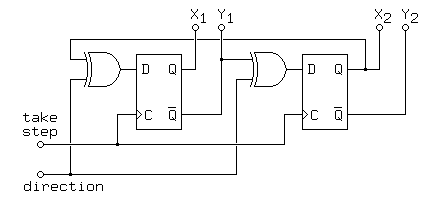
A number of manufacturers of stepping motor control circuitry make integrated circuits that include slightly more complex logic allowing both full and half stepping modes. For example, the Motorola (and others) MC3479 chip includes a 16 volt 350mA H-bridge and control logic with step, direction, and mode inputs to control half-stepping.

The SGS-Thompson (and others) L297 includes just the mid-level control logic for full or half-step control of a pair of H-bridges used to control a permanent magnet or variable reluctance motor. This chip is specifically designed to control the L298 dual 2 Amp H-bridge, and in addition to the mid-level control logic, it includes the one-shots and comparators required to use this H-bridge as a current limited chopper.

Software Solutions

If a microprocessor, programmable interface controller or other computer system is used to control a stepping motor, the computer can directly generate the control vector in software and present it to the motor interface through a parallel output port, as shown in Figure y.4:

Figure y.4 

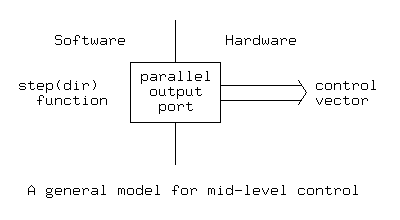
The control trajectory for any motor can be described as a circular array of control vectors. The simple full-stepped trajectory given in the introduction can be represented as:

t, a 4 element array where

t[0] = 10
t[1] = 9
t[2] = 6
t[3] = 5

t, an 8 element array where

t[0] = 10
t[1] = 8
t[2] = 9
t[3] = 1
t[4] = 5
t[5] = 4
t[6] = 6
t[7] = 2

The step routine itself does not depend in any way on the control vector. For all of the above examples, the step routine is:

p, a statically allocated integer variable, initially zero.

step( d )

-- a function of one argument d
-- where d must be either +1 or -1
-- no value is returned

p = p + d ( mod size( t ) )
output( t[p] )

Note that, when translating the above code into real programming languages, the simple use of the mod operator above can rarely be preserved. Mathematicians generally agree that

y > x ( mod y ) > 0

Simple Practical Examples

The following C code will control a single 3-phase variable reluctance motor taking its control vector from the three least significant bits of the parallel port of a Unix or Linux system, assuming that the parallel port has been opened in the correct mode using the file descriptor pp:

    #define STEPS 3
    int t[STEPS] = { 1, 2, 4 };

    int p = 0;

    void step( int d )
    {
        char c;
        p = (p + STEPS + d) % STEPS;

	/* output t[p] using low-level Unix I/O */
        c = t[p];
        write( pp, &c, 1 );
    }

    #define STEPS 8
    int t[STEPS] = { 10, 8, 9, 1, 5, 4, 6, 2 };

An Object Oriented Design

Things are more complex if multiple motors are in use! Although ad-hoc solutions can are common, a systematic approach is appropriate, and even in languages with no support for object oriented methodology, the easiest way to describe such solutions is in object oriented terms.

After initialization, which may depend on many low level details, the high level software isn't interested in how the motor works. Therefore, for each motor object, the visible interface needs only the step function. The class of motor objects is polymorphic because the details of how step operates for one motor may differ considerably from the details of how it works for another.

The following code is given in Java; translation to C++, Simula 67 or other object oriented languages should be straightforward:

    abstract class StepMotor
    {
        public abstract void step(int d);
            // step the motor in direction d (+1 or -1)
    }

    class UniversalStepMotor extends StepMotor
    {
        private int s;         // the size of the trajectory
        private int[] t;       // the trajectory for this motor
        private int p;         // motor's position in trajectory
        private OutputStream o;// the output port to use

        public void step(int d)
            // step the motor in direction d (+1 or -1)
        {
            p = (p + s + d) % s;
            o.write( t[p] );
        }

        public UniversalStepMotor( int[] table, OutputStream out )
	    // initializer
        {
	    s = table.length;
            t = table;
            p = 0;
            o = out;

            o.write( t[p] );
        }
    }

Given that MotorPort is an object of type java.io.OutputStream, the following Java code will create a UniversalStepMotor object m for a 3-phase variable reluctance motor:

    StepMotor m = UniversalStepMotor(
        new int[] {4,2,1}, // step table for the motor
        MotorPort          // OutputStream for the motor
    );

For many applications, the class StepMotor defined above will need to be extended with a reset procedure, used to reset both the motor object and the motor interface. This procedure should probably be incorporated directly into the definiton of the StepMotor class, as opposed to adding it by class extension. This procedure would typically be called as the first step in recovering from an error detected at higher levels in the control hierarchy.

When Objects Won't Do

For programmers who can't use object oriented design, for any reason, the following exmaple illustrates an appropriate mid-level design that avoids the use of such features. Using Pascal, the following types can be used to describe each motor:

    type
        direction = -1 .. +1;

        trajectory = array [0 .. MaxTrajectorySize] of int;

        StepMotor = record
            s: integer;    { size of this motor's trajectory }
            t: trajectory;
            p: integer;    { this motor's position in trajectory }
            o: port;       { the output port to use for this motor }
        end { record };

Given the above definitons, we can now construct a general purpose step procedure:

    procedure step(var m: StepMotor, d: direction);
        { step motor m in direction d }
    begin
        with m do begin
            p = (p + s + d) mod s;
            output( o, t[p] );
        }
    end { step };

In effect, in abandoning programming languages with direct support for object orientation, we have had to chang our notation from:

    motor.step( dir );

    step( motor, dir );