Motors

Introduction
This section contains information about implementing dc motors in a mechanical system, such as those that are typically encountered in ME 3110. Although there is some limited information on stepper and other, specialized types of motors, primary emphasis is placed on DC permanent magnet motors, since these motors are the most common, least expensve, and lightest type of motors.



Contents

Types of Motors
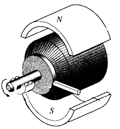
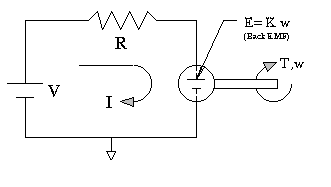
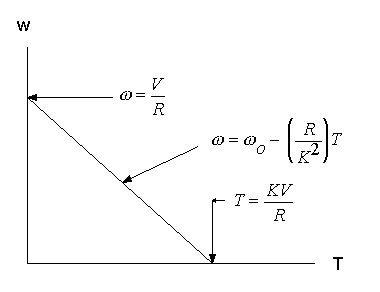
The Theory of Permanent Magnet DC Motors
Characterizing Motors in Practice
Places to find motors
Common Problems when using Motors
References

Types of motors
There are several different types of dc (dirrect current) motors that are available. Their advantages, disadvantages, and other basic information are listed below in tabular form.

Type	Advantages	Disadvantages
Stepper Motor	Very precise speed and postion control. High Torque at low speed	Expensive and hard to find. Require a switching control circuit
DC Motor w/field coil	Wide range of speeds and torques. More powerful than permanent magnet motors	Require more current than permanent magnet motors, since field coil must be energized. Generally heavier than permanent magnet motors. More difficult to obtain.
DC permanent magnet motor	Small, compact, and easy to find. Very inexpensive	Generally small. Cannot vary magnetic field strength.
Gasoline (small two stroke)	Very high power/weight ratio. Provide Extremely high torque. No batteries required	Expensive, loud, difficult to mount, very high vibration.

Almost without exception, dc permanent magnet motors are by far the best choice for ME3110 projects. Their small size, compactness, and common availability make them a good choice on almost any machine that doesn't require a huge amount of power output.

Because permanent magnet motors are so commonly used, the rest of this section will be dedicated to their operation and application.

Elementary Theory of DC Permanent Magnet Motors

Since this type of motor uses a permanent magnet to generate the magnetic field in which the armature rotates, the motor can be modeled by the electrical circuit in the armature alone. If we further simplify the circuit by ignoring the inductance of the armature coil, we arrive with the following circuit diagram for a simple motor:


V is the voltage supplied by the power source (usually a battery), and R is the resistance of the motor's armature coil. This resistance cannot be measured at rest, since it changes as speed increases towards the steady state speed. Kirchoff's voltage law leads to the following equation:



By examining the effect of the magnetic field in the motor, and realizing that magnetic flux is constant, we can arrive at the following two equations relating the torque and speed output of the motor to the supplied current and voltage:


These are often known as the transducer equations for a motor, since a motor is really an electro-mechanical transducer. The constants Kv and Km are dependent on the particular motor, but if they are expressed in SI UNITS, their values are always equal, thus



It is important to remember that, in this equation, T is the total torque acting on the motor, and is generally non-zero even with no applied load, due to the internal losses in the motor. This equation implies that the speed of the motor is equal to some constant, which is a function of the applied voltage and the motor constant, minus another constant times the applied torque. This is an important relation, since it reveals that for this motor model, Torque is a linear function of speed If torque is plotted vs. speed for a motor, the plot will typically look like this:



The intercepts of the line at the T and w axes are especially important, since they give the values of the stall torque and the no-load speed.The stall torque is the torque which the motor provides when the rotor of the motor is held at zero velocity. It is not difficult to derive from the diagram holding speed and torque, respectively, at zero, that:



It is very important to note that in our development, we have included the Torque on the motor, T, as only one term, which includes both a load torque and the torque that is provided by the bearings of the motor and the frictional losses within the motor. The consequence is that, in practice, the torque on the motor is never really zero, and the no-load speed is really only approximately given by the relation above. Similar arguments apply to the stall torque, although in this case the difference is much smaller since there are no frictional losses in a motor when the speed is zero.

Since we commonly find the no-load speed given when we buy a motor, we can substitute the no-load speed into the general equation above and find a bit more useful relation for the loaded speed of a motor:



Finally, by taking the derivative of this equation with respect to power, we can find that the maximum power that can be output by the motor is given by the relation:

This equation is especially useful when evaluating how large a motor might be required for an application.


Limitations of this motor model

There are several assumptions that we have made in the development of this model, which are very important to keep in mind when using the above relations to implement a dc permanent magnet motor:

1. The torque on the motor has all been lumped into one term, which includes the torque provided by the bearings of the motor and other frictional losses. The consequence of this assumption means that in general, the no-load speed will only approximately be given by the relation w=V/K, since in practice a small, non-zero frictional load is always present.
2. We have assumed that the inductance of the motor is zero, which is normally a good assumption (especially for steady state), but must be re-evaluated if transient response of the motor is to be analyzed.
3. We have assumed that the resistance of the motor is constant, which is ideally not true. The resistance of the motor acutually changes slightly with speed, and also with temperature. These changes are normally small, however, so this is a valid assumption unless the motor is operating at very high temperatures
4. We have assumed in the development that we acutually know the motor constant, K, and the resistance, R, which is in general NOT the case. The motor specifications section is devoted to characterizing motors given information which we in practice are able to obtain.

Motor Specifications

Normally, when you obtain a motor from a commercial source, you will not immediately know all the information necessary to characterize the motor in terms of the theoretical development above. Some motors include the Stall Torque, the no-load speed, and the Resistance, while others include only the rated voltage and the power output at maximum power. In these cases, there are several things you can do to experimentally determine the motor constant, internal resistance of the motor, etc. Here are some basic steps to take to characterize your motor:

1. Look on the package of the motor, and obtain all the information you can from there. Then use the given information in the above equations to calculate the values of K, R, or other values that you don't know. For example:
   
   
   • Usually at least the Voltage and the no-load speed are given. If they are, you can use the above equations to caculate K=w*V. Be sure to use the correct units.
     
     
   • If the stall torque is given, and you have already found K from step 1, you can find the value of R, the internal resistance of the motor.
   
   If the package of your motor does not contain the information you need, you can always contact the manufacturer, who will be able to give you all the details of the motor that you require.
   
   
2. If step one did not yield enough information to calculate all the parameters, you can test the motor to find some of the values yourself:
   
   
   • Use an ammeter(measures current) to measure the current the motor draws. Apply a voltage to the motor, and allow the motor to run with no load. Measure the no load current. From above, knowing K, the motor constant, we can calculate the friction torque, Tf, on the motor is I(no load)*K. This torque is present at all times when the motor is running. (It is actually not constant with speed, but it is small, and we can assume without much loss in accuracy that this is the case).
     
     
   • If you have access to a tachometer, measure the no-load speed, and from the measured Voltage applied calculate K. You can also measure the no-load speed if you have a strobe light by adjusting the strobe period until the motor appears to "stand still".
     
     
   • Attach a large gear to your motor, and hang a weight from a string that will be wrapped up as the motor turns. At the bottom of the string, hang an object of known mass, or a cup that can hold water. Then, apply a voltage, and continue to increase the voltage until the motor just supports the weight of the object. By calculating the weight of the object and the radius of the gear, you can calculate the stall torque of the motor. You know the Voltage applied, so from the relations above you can then calculate (since w=0) that R=Tstall/(K*V). This type of test is called the locked rotor test. Another way to perform this test is by applying a constant voltage and varying the applied weight until the stall torque is reached.
     
   
   
3. Finally, if you cannot obtain the information from the motor itself, and for some reason you cannot obtain the information using the above tests, you can get an idea of the performance of your motor by using information from other motors. For example, if another motor where you got yours has the internal resistance, you could guess that the resistance of your motor is similar, and make the rest of your analysis more conservative to account for the error.

Finding Motors
DC permanent magnet motors are widely available and relatively inexpensive. Below is a list of some common places to find motors, along with a brief description of the types of motors you can expect to find there:

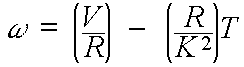
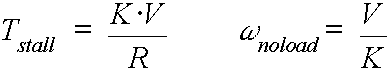
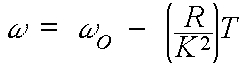
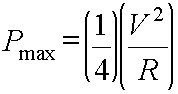
Supplier	Selection	Types of Motors Available
Radio Shack	Good	Small motors from 3-12V. Most are less than $10.
Hobby Stores	Good	9-18V motors- Most made to run on multi-cell rechargeable battery packs. Most are $20-$40. Generally pretty powerful motors.
Electric Screwdrivers	Fair	Very compact, high torque motors. Recharger, batteries, etc, are all included. Also has a planetary gear train too. Most are $20-$30.
Vendor Catalogs	Excellent	Many different available. Must normally wait for shipping and handling, and sometimes there is a minimum order. See www links for a URL's of some vendors to get free catalogs..
Toy Stores	Poor	Motors available in various, small motorized toys. These motors normally very small, and run on 3V or 6V at the most..

Common Motor Application Problems

Problem:

Our motor doesn't have enough power to perform the necessary task in our machine, but we have already bought the motor: what can we do?

Solution:

From a conservation of energy standpoint, if you don't have enough energy out of the system, add more into the system. In other words, increase the size of your batteries. If you add more batteries in series with the ones you already have, you will give the motor a higher top speed. On the other hand, if you need more torque, you can add more batteries in parallel with the existing ones, and your batteries will provide more torque at the same voltage. This is the way to go if your batteries are already supplying the rated voltage to the motor. Another obvious solution is to reduce the load on the motor.

The final, and most commonly implemented solution to this problem is to use a gear train to gear your motor down or up. You can gain torque or speed at the expense of the other. (See Gears).

Our machine works ok, but it drains the batteries very quickly. Batteries are getting expensive! What do we do?

Batteries are rated for a certain number of amp-hours. Alkaline batteries will typically have a larger rating than rechargables, for example. An amp-hour rating of 9 means that the battery can supply 1 amp for 9 hours, or 9 amps for 1-hour, or anywhere in between. If you know the characteristics of your motor (see the motor specifications section), you can calculate the current that your motor is drawing, and from the amp-hour rating of your batteries, you know how long they will last. Because it is more of an issue with rechargables, they are more likely to supply this information when you purchase them.

There are two solutions to this problem: reduce the load on the motor so that it draws less current, or get more batteries so that your battery pack can supply the same amount of current longer. Keep in mind that adding a gear train will in general NOT cure this problem, since the amount of power that is consumed by the motor will be the same. If your machine was alreading moving forward, adding a gear train will reduce the torque load on the motor, but the vehicle will move faster, and the motor will end up consuming the same amount of power. (Actually, the gear train will have some losses, and you might actually make the problem worse!)

We are still in the design phase, and have no good idea how big of a motor we need to buy, or how big the batteries should be. What is a good way to figure this out?

The answer to this very common problem is not trivial- that's why it's a common problem. The following steps might help you make a good guess:

1. Gather the most complete and specific information you can about the task that the motor will need to perform. For example, get a good guess at the size of the machine, the angle of the incline it will need to climb, the amount of time it will run, the torque the motor will need to provide. If you can't quantify the applicable variables, then make a conservative 'best guess'.
   
   
2. Use the information gathered in (1) and physical relations to calculate the power that will be necessary, the torque that will be necessary, the time required, or whatever items are applicable.
   
   
3. Compare the information calculated in (2) to available motors and batteries. Start by finding the power you need, and then choose a voltage that is commonly available. Then use conservation of energy and the power equation in the theory section to calculate how much current the motor might draw at this voltage. Finally, multiply this current by the time of operation and find the rating of the battery that might be required.

1. Shigley, J.E, and Mischke, C.R., Mechanical Engineering Design, 5th Ed., McGraw-Hill, New York 1989. (The ME4180 textbook, available at the bookstore or the Georgia Tech Library.)
2. Buchsbaum, Frank, Design and Application of Small Standardized components Data Book 757 Vol. 2, Stock Drive Products, 1983 (Free copies available at Stock Drive Products).

WWW links

Stock Drive Products Free design guides and a large number of mechanical components available here
Boston Gear Division Another gear Vendor
AutoMationNET List of several vendors for a comprehensive list of mechanical components.
List of Mechanical Engineering Vendors

[ Finding Motors || Basic Theory || Common Problems || Motor Specifications ]

[ Gears || Where am I? || Element Index || ME 3110 Page || Electrical Components ]
Created and Maintained by David H. Cowden. gt0199f@prism.gatech.edu