Diseño de un

Controlador Fuzzy Adaptivo

para el control de un péndulo invertido

Iván Socolsky

Rodolfo Campero

Cátedra de Inteligencia Computacional

Facultad de Ciencias Exactas y Tecnología

Universidad Nacional de Tucumán

Indice

Introducción

Links

Home Page de trabajos de Inteligencia Artificial

Este trabajo en formato pdf

Curriculum Vitae de Rodolfo Campero

Curriculum Vitae de Iván Socolsky

Enviar e-mail a Rodolfo Campero o a Iván Socolsky

Introducción

El presente trabajo tiene como objetivo mostrar las técnicas de sistemas expertos basados en reglas y redes neuronales de retropropagación (ambos de tipo fuzzy) y la combinación de ambas técnicas para la construcción de un controlador adaptivo.

Se aplican estas técnicas al conocido problema del péndulo invertido al construirse una aplicación de fácil uso diseñada especialmente para ilustrar estos conceptos y para realizar simulaciones.

Finalmente, se comparan los resultados y se obtienen conclusiones al respecto.

Planteo del problema

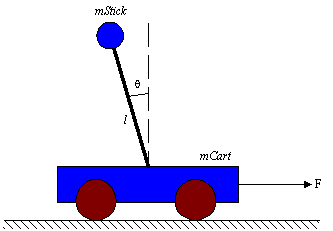
El sistema que se intenta controlar consiste de un carro que tiene adosada una varilla en cuyo extremo se encuentra un cuerpo de cierta masa.

El carro solo puede moverse hacia delante y hacia atrás en una línea recta, al aplicársele una fuerza F.

La varilla está unida al centro del carro mediante una juntura sin rozamiento, que le permite girar sobre un eje situado en la juntura y con un grado de libertad sobre el plano determinado por la dirección de movimiento del carro y la normal al suelo.

Puede considerarse que la varilla no tiene masa.

Los datos del problema son la masa del carro y del extremo de la varilla, la longitud de la varilla, y el ángulo y la velocidad angular.

Se necesita controlar la fuerza F para llevar la varilla a posición vertical, pudiendo conocer el ángulo y la velocidad angular en cualquier momento. El ángulo y la velocidad angular inicial pueden ser cualesquiera dentro de los rangos que la solución especifique (para un dado valor de F máxima); los parámetros tales como mCart, mStick y l pueden variar de un caso a otro.

Esquema general y arquitectura de la solución

A continuación se esquematiza el controlador en su entorno operativo. Más adelante se describirán cada uno de sus componentes constitutivos.

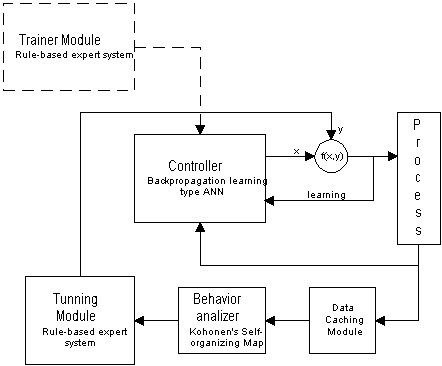
El sistema está centrado en el módulo Controller que está implementado con una red neuronal de tipo backpropagation. Esta red debe entrenarse previamente. Para este fin, puede utilizarse el sistema experto mostrado en la figura en líneas punteadas o bien puede utilizarse algún método de datamining si es que no se dispone de conocimiento experto y se tiene acceso a información acerca del sistema (en forma de mediciones).

Al comenzar el ciclo normal de operación, el Controller recibe datos del proceso (a través de sensores) y los propaga a través de la ANN para obtener la salida. Simultáneamente, las variables medidas del proceso son almacenadas en un bloque Data Caching Module y utilizadas para alimentar un reconocedor de patrones del tipo de un SOM de Kohonen. Este mapa (Behavior Analizer) ha sido previamente alimentado con diferentes patrones tomados del proceso y es capaz de describir comportamientos del mismo en el tiempo: "converge rápidamente", "converge lentamente", "diverge", "oscila", etc. Una vez que se ha encontrado el comportamiento del sistema, se procede a ajustar el comportamiento natural por medio de un tunning que es realizado por el módulo que contiene el sistema experto (Tunning Module). La salida de este último módulo también es utilizada para realimentar a la ANN del controlador y así poder hacer que el sistema se adapte al nuevo entorno.

Red Neuronal

Se utilizó una red de retropropagación para construir el eje central del controlador. Como se disponía de un controlador funcional basado en sistemas expertos fuzzy, se diseñó la red mapeando las reglas de la base de conocimiento en un conjunto de neuronas interconectadas.

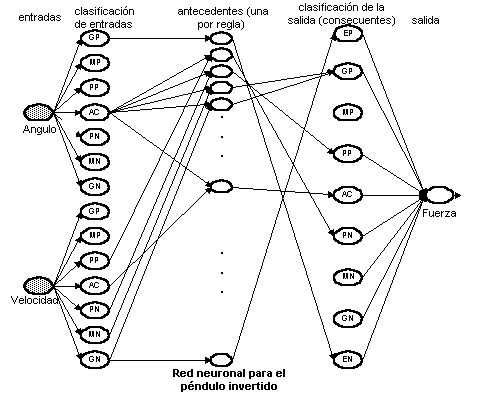
La red Controller tiene 4 capas. La primera capa consta de 14 neuronas que clasifican a las variables de entrada (ángulo y velocidad) en los conjuntos fuzzy utilizados en el sistema experto; la segunda, de 35 neuronas, representa los antecedentes de las reglas; la tercera, de 7 neuronas, representa la clasificación de la variable de salida y la cuarta, de 1 neurona, es la capa de salida de la red.

Los círculos grises de la figura no son neuronas, sino interfaces de entrada a la red.

Con respecto al entrenamiento, este se realizó utilizando las salidas del Training Module para dos casos (simétricos entre sí), ambos simultaneamente. Se entrenó hasta obtener una diferencia de 0.07 entre la salida de la red neuronal y la del sistema experto (en una escala de 0 a 1). Esto llevó aproximadamente 5 minutos (procesador Celeron 333Mhz) con una velocidad de aprendizaje igual a 0.2. El caso de entrenamiento fue el siguiente:

mCart = 10 kg.
mStick = 1 kg.
l = 1 m.
q = 43º; caso simétrico q = -43º.
dq / dt = 0º/seg.
F_max = 100 N

Módulo de entrenamiento

El Training Module es el encargado de darle a la red el entrenamiento necesario para trabajar bajo condiciones preestablecidas. Este conocimiento es obtenido a su vez de un sistema experto diseñado para trabajar en estas condiciones.

En cuanto al controlador, se trata de un sistema experto basado en conjuntos fuzzy cuya configuración es la siguiente:

Funciones de pertenencia

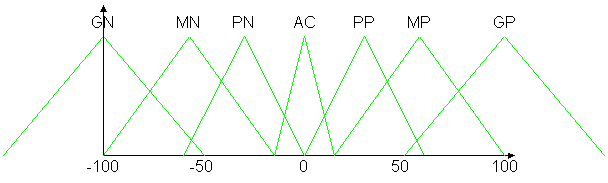
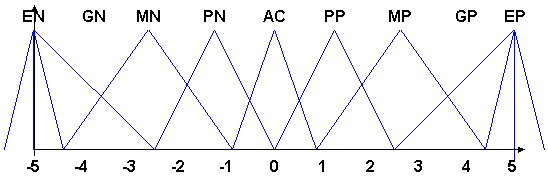
A continuación se grafican las funciones de pertenencia a los conjuntos fuzzy referidos a la variable ángulo. Las unidades en el eje horizontal son grados.

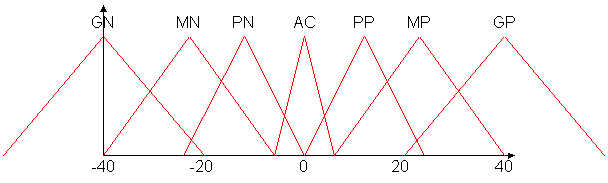
Los conjuntos de pertenencia son GN = grande negativo, MN = mediano negativo, PN = pequeño negativo, AC = aproximadamente cero, PP = pequeño positivo, MP = mediano positivo, GP = grande positivo.

Las funciones de pertenencia correspondientes a la variable velocidad angular se grafican a continuación. Las unidades son grados por segundo y los nombres de los conjuntos son los mismos que en el caso anterior.

Función de defuzzificación

Las funciones de pertenencia son las siguientes:

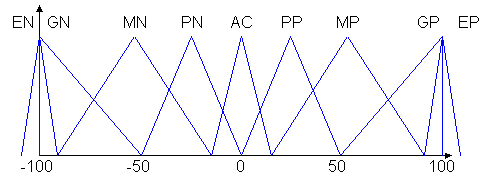
Los nombres de las funciones son los mismos que las funciones de fuzzificación, además se agregaron EN = enorme negativa y EP = enorme positiva.

Los valores de la fuerza se indican en newtones.

La defuzzificación se realiza con el método del centroide.

Reglas del sistema

Se presentan las reglas del sistema experto. Las variables son: a = ángulo, v = velocidad, f = fuerza. Los conjuntos de pertenencia son GP = grande positivo, MP = mediano positivo, PP = pequeño positivo, AC = aproximadamente cero, PN = pequeño negativo, MN = mediano negativo, GN = grande negativo. En el caso de la fuerza se agregan dos conjuntos más; estos son EP = enorme positivo y EN = enorme negativo.

Módulo de sintonización

La labor del Tunning Molule es monitorear el comportamiento del sistema con el fin de detectar la divergencia del sistema (en caso de que ocurra) y modificar la salida sugerida por el Controller para corregir la situación, o intentar mejorarla en caso de que converja. La salida real hacia los actuadores (que queda determinada por la suma de las fuerzas sugeridas por el Controller y el Tunning Module) se retroalimenta a la red neuronal del Controller como verdadero valor para las condiciones dadas en ese instante.

Este bloque es otro sistema experto cuya configuración es la siguiente:

Funciones de pertenencia

Se presenta una gráfica de las funciones de pertenencia. El eje horizontal indica el valor de la variable en su unidad de medida. Las variables que intervienen son angle (última medición del ángulo, en grados) y delta (diferencia entre la medición del ángulo actual y la anterior, en grados por segundo).

Las funciones de angle son las siguientes:

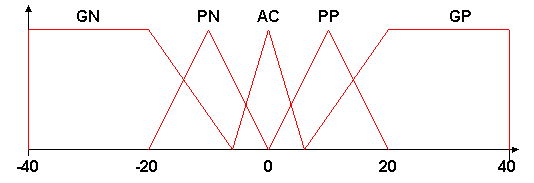
Las funciones de delta son las siguientes:

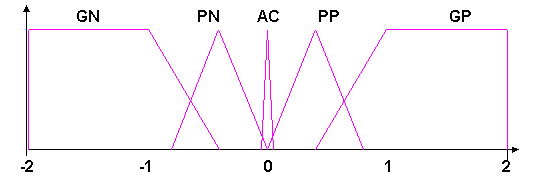
Función de defuzzificación

Las funciones de pertenencia son las siguientes:

Los nombres de las funciones de pertenencia son los mismos que los del Training Module.

Los valores indicados en la figura son los valores de fuerza en newton.

La defuzzificación se realiza con el método del centroide.

Reglas del sistema

Se presentan las reglas del sistema experto. Las variables son: a = ángulo, d = delta. Los conjuntos de pertenencia son EP = enorme positivo, GP = grande positivo, MP = mediano positivo, PP = pequeño positivo, AC = aproximadamente cero, PN = pequeño negativo, MN = mediano negativo, GN = grande negativo, EN = enorme negativo.

Analizador de comportamiento y almacenamiento de datos

Los módulos Behavior Analizer y Data Caching Module generan las entradas del sistema experto del Tunning Module. El Data Caching Module, en esta implementación, consiste en una variable que contiene el valor de la última medición del ángulo. Por otra parte, el Behavior Analizer le resta a la medición actual del ángulo su última medición para obtener la diferencia delta.

Las variables angle y delta son las únicas necesarias para que el Tunning Module realice su tarea.

En un problema de mayor complejidad, puede ser necesario implementar el Data Caching Module como un buffer que almacene varias mediciones no necesariamente consecutivas, y el Behavior Analizer como una SOM de Kohonen que clasifique el comportamiento del proceso en alguno de los patrones con los que fue entrenada.

Programa de aplicación

Se construyó un programa de aplicación que implementa el diseño antes expuesto, que permite al usuario ingresar distintos valores a las variables intervinientes.

Además permite escoger entre un controlador basado en redes neuronales y uno basado en sistemas expertos. Para ambos permite activar y desactivar el módulo de corrección de fuerza (Tunning Module).

Para el caso de la red neuronal, permite escoger entre tres posibles velocidades de aprendizaje: rápido (velocidad de aprendizaje = 0.5, incidencia del corrector = 2), normal (velocidad de aprendizaje = 0.3, incidencia del corrector = 1) y lento (velocidad de aprendizaje = 0.1, incidencia del corrector = 0.5).

La incidencia del corrector (factor de multiplicación de la fuerza agregada por el corrector) cuando trabaja el sistema experto es de 10.

Se brinda la posibilidad de hacer zoom para tener mayor detalle en aquellas zonas de las curvas donde las variables se aproximan a cero, además de indicar los valores correspondientes a los puntos de las curvas que señale el cursor.

A continuación se presenta la salida de la aplicación en un caso de uso:

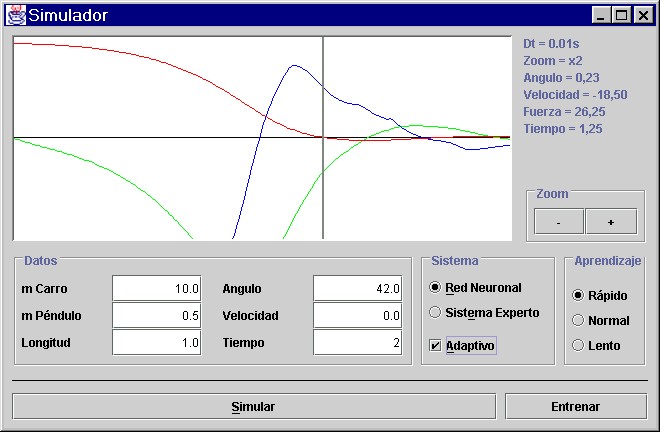
El sistema fue diseñado utilizando modelado orientado a objetos y el código fue escrito en Java versión 1.2 de Sun Microsystems.

Resultados de simulaciones

Consideramos primero aquellos casos que están dentro de la gama de casos que el sistema experto puede considerar, esto es, todos aquellos en los que la masa del carro es igual a 10 kg, la de la varilla 1 kg y su longitud 1 m. En estas circunstancias, el comportamiento del sistema experto es superior al de la red neuronal en las primeras ejecuciones; con el tiempo la red evoluciona al punto de alcanzar (y hasta superar) la calidad del sistema experto.

Consideramos que el sistema convergió cuando el valor absoluto del ángulo cae por debajo de 1 grado sin superarlo después durante el resto de la simulación.

En las condiciones mencionadas, con un ángulo inicial de 40º, velocidad angular inicial igual a 0º/s,el tiempo de convergencia para el sistema experto sin Tunning Module fue de 1,56 s; con el Tunning Module activado fue de 1,15 s.

En el caso de la red neuronal (adaptiva), se obtuvo la siguiente tabla (siempre se trabajó con una red con entrenamiento mínimo para la ejecución número 1):

Condiciones:

Masa del carro 10 kg
Masa de la varilla 1 kg
Longitud 1 m
Angulo inicial 40 º
Velocidad inicial 0 º/s

Resultados:

El salto brusco en los valores de la tabla para el caso de aprendizaje rápido (número de ejecución 20 al 30) se debe a que una pequeña oscilación del ángulo superaba 1º en valor absoluto en su pico, lo que obligaba a considerar la convergencia después de la oscilación; una vez que el sistema controló la oscilación, se pudo tomar el tiempo antes de la oscilación.

Se muestran gráficas que ilustran los resultados anteriores (en todos los casos, el tiempo de sampleo fue de 2 segundos):

Código de colores utilizados:

Angulo
Velocidad
Fuerza

Sistema experto con corrector

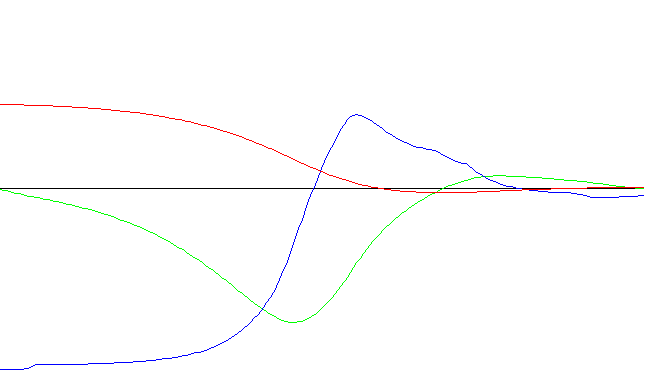
Red neuronal con aprendizaje rápido - Ejecución nro. 1

Red neuronal con aprendizaje rápido - Ejecución nro. 32

Cuando las condiciones del proceso cambian (la masa del carro o de la varilla, o la longitud de esta última), el sistema experto no puede controlar el péndulo aunque el ángulo inicial sea tal que la fuerza disponible sea suficiente para hacerlo.

Se presenta el caso con las siguientes condiciones:

Masa del carro 20 kg
Masa de la varilla 1 kg
Longitud 1 m
Velocidad inicial 0 º/s

En este caso, el primer ángulo entero que el sistema experto adaptivo no puede controlar es 25º. Se presenta una tabla con los valores obtenidos la utilizar red neuronal con las condiciones mencionadas y este ángulo inicial:

Al realizar estas simulaciones pudo apreciarse en las gráficas que cuanto más veloz es el aprendizaje, más irregular es la curva que describe la fuerza; inclusive oscila. En algunos casos las oscilaciones se hacen de mayor amplitud a medida que el tiempo avanza. Las curvas para aprendizaje más lento son más suaves.

Gráficas ilustrativas (tiempo total de sampleo: 5 seg.):

Sistema experto con corrector

Red neuronal con aprendizaje rápido - Ejecución nro. 1

Red neuronal con aprendizaje rápido - Ejecución nro. 2

Red neuronal con aprendizaje rápido - Ejecución nro. 5

Red neuronal con aprendizaje rápido - Ejecución nro. 36

El sistema se comporta adecuadamente aún en situaciones más extremas, como la que se presenta:

Masa del carro 55 kg
Masa de la varilla 10 kg
Longitud 1 m
Angulo inicial 5 º
Velocidad inicial 0 º/s

Los resultados:

En este caso, la velocidad de aprendizaje fue bajando a medida que el sistema necesitaba menos ayuda. Esto ayuda utilizar más eficientemente la fuerza.

A continuación se presentan las gráficas (sampleo: 10 segundos):

Red neuronal con aprendizaje rápido - Ejecución nro. 1

Red neuronal con aprendizaje rápido - Ejecución nro. 35

Red neuronal con aprendizaje normal - Ejecución nro. 46

Red neuronal con aprendizaje lento - Ejecución nro. 57

Una característica que es remarcable es el comportamiento de la red neuronal durante el entrenamiento ante los casos extremos. Cuando se ingresa por primera vez una condición extrema a una red neuronal con entrenamiento mínimo, es probable que esta nunca aprenda a dominar el proceso; un ejemplo sería la configuración anterior con masa del carro igual a 60 kg en lugar de 55 kg. Sin embargo, si se entrena la red con casos de dificultad creciente, paso a paso, sin avanzar hasta que no domine una situación, la red aprenderá este caso que al principio parecía imposible. Con este método se llegó a levantar más de 100 kg en las condiciones del caso anterior (notar que con mínimo entrenamiento nunca pudo aprender a levantar 60 kg).

Asimismo, una vez que el sistema aprendió a controlar un caso, el caso simétrico (el que se obtiene al multiplicar por -1 el ángulo y la velocidad iniciales) es controlado en menos iteraciones.

En todos los casos, el sistema nunca deja de poder controlar los casos más sencillos (o sea, los más similares a las condiciones del entrenamiento básico).

Conclusiones

Las simulaciones ilustran el comportamiento del controlador ante distintas situaciones. Del estudio de estos resultados, se puede concluir que la implementación de un sistema de características similares a este en un entorno real requeriría de un dispositivo (tal vez parte del Behavior Analizer) que automáticamente ajuste la velocidad de aprendizaje. De esta manera, durante los primeros momentos de la interacción del sistema con un proceso de características desconocidas el controlador manejaría la situación sin que el proceso colapse; una vez que el sistema esté bajo control, bajaría la velocidad de aprendizaje cada vez más de manera tal que se economice en energía al optimizar la aplicación de la fuerza (o la variable que se esté controlando) y el comportamiento del controlador sea más suave.

Otra conclusión importante es que el controlador trabaja mejor en aquellos procesos donde los cambios en el entorno son menos bruscos.

Aparentemente, si en un proceso determinado existe la posibilidad de controlar una situación extrema con las limitaciones impuestas a las variables controladas, la red neuronal encontrará la manera de hacerlo (aunque requiera entrenamiento de manera tal que el entorno se aproxime gradualmente a esta situación límite).

En general, modelo presentado es ampliamente superior a un controlador basado en un solo sistema experto; su ventaja radica en su adaptabilidad una vez instalado y trabajando en un ambiente real.