V.A.Kaimanovich (1), E.M.Krupitski (2) and A.V.Spirov (3)1) Department of Mathematics and Statistics, University of Edinburgh, Edinburgh EH9 3JZ, Great Britain 2) Research Laboratory of the Regional Narcological Center, St.Petersburg, Russia 3) I.M. Sechenov Institute of Evolutionary Physiology & Biochemistry St.Petersburg, Russia
Connections between the activity of ionic pumps/channels and the cell form were discussed by many authors who observed shape changes at the same time as activation of memebrane pumps (25). At present, a number of electrically active membrane enzymatic systems with lateral diffusion of components is known which could play the role of generators of the electric pattern of the cell surface (i.e., of the cell electric polarity). In the first place one should mention here systems of assemblage of ionic channels and ionic pumps from laterally diffusing molecular components, systems of ionic channels and ionic pumps and their natural modifcators and inhibitors (26, 27, 28).
For modelling of the interactions between the membrane electric activity and sub-membrane cytoskeletal components we use a generalization of Fromherz' model of self-organization in the system of ionic channels in biomembranes (24, 29, 30).
According to this model, electrically charged channels in a fuid membrane may form dissipative structures driven by a concentration gradient of salt. On a molecular level the effect is due to dissipative attractive forces; the channel currents induce local gradients of the membrane potential that interact with the protein charge. The ion flow through each channel induces a halo of lateral current and a radial gradient of electric potential. Other channels are attracted if the sign of the charges is matched to the polarity of the ion current. Around a transient cluster, however, the gradients are superposed such that drift may overcome Brownian motion. As a result, a macroscopic pattern may arise from the fluctuation. This self-organization by charged channel condensation is treated by a coupled system of equations: Smoluchowski's equation describing diffusion and drift of the membrane channels (dynamics of the channel density N) and Kelvin's equation describing the dynamics of the membrane potential V.
Equations of the model describe dynamics of the membrane electric
potential V and of the ionic channel density N on
the membrane surface (in dimensionless variables):
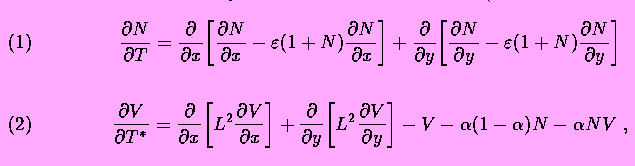
where x and y are space coordinates, 
;
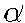and L are parameters,
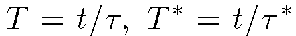with 
,
being time intervals, and t
is the physical time.
In order to formalize the connection between the membrane electrical activity and the cell form, we add to Fromherz' model an equation which describes the above property of membrane generated intracellular fields to determine space orientation of MT assemblage in the submembrane layer of the cytoplasm, so that the higher is the local membrane potential, the "more oriented" are MT. As we have discussed above, the reason for MT orientation in submembrane layers of the cytoplasm is a suffciently high value of the potential V of the intracellular electric field. Under condition that the local stationary value of V is greater than a given threshold critical value V cr , we have used the following empirical formula connecting the behaviour of parameter ff with the over-critical value V>Vcr :
where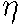 
is a constant coeffcient.
The dimensionless parameter 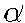has
the form
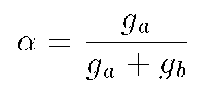where g(a)
is the channel conductivity , and g(b)
is the conductivity of membrane matrix proteins (24). So,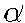
increases when either the channel conductivity g a increases or
the conductivity of membrane matrix proteins g(b)
decreases.
According to Fromherz, changing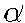
prompts instability (24). Thus, locally high membrane electric
potential values lead to creation of the regions in the submembrane
layer with a high local directionalization of MT bundles. In their
turn, these regions with MT mostly perpendicular to the membrane
inner surface change local conductivity of matrix membrane proteins
or local channel conductivity (see equation (3)), thereby leading
to a loss of stability of the steady membrane electric pattern.
As a result, the membrane electric pattern is changed into a new
stable one, which, in its turn, reorganizes the structure of the
submembrane cytoskeleton.
Get your own Free Homepage