Alexander V. Spirov
Institute of High Performance Computing and Data Bases
Sechenov Institute of Evolutionary Physiology & Biochemistry; S.-Petersburg; Russia
The problem of how the information coded in linear DNA molecules becomes translated into a three-dimensional form we treat from the viewpoint of Pattern-Form Interplay Models. The characteristic feature of these models is the feedback loop from (bio)chemical pattern formation to modeling embryo form changes. In accordance with the model the system is open and changes in a pattern give rise to changes in form and these changes in form (surface geometry) cause further pattern changes, and so on. Spontaneous pattern formation takes place in the model as primary and secondary bifurcations of non-linear parabolic PDEs describing reaction-diffusion systems with imposed gradient. We consider phenomenon of axis tilting as the case of symmetry breaking via secondary bifurcations. Besides that we describe a new case of bifurcation in the reaction-diffusion system. It occurs as a result of gradually decreasing of reactants concentrations and assumes the description not in a terms PDEs but as a stochastic simulation of a few particle ensemble. The explicit demonstration of this phenomenon is believed to be new.
Nowadays morphogenesis is becoming a commonly used term in some interdisciplinary fields. This term reflects general ideas of structure formation governed (directly or indirectly) by sets of rules or algorithms [Mjolsness et al., 1991; deBoer et al., 1992; Cangelosi et al., 1994; Dellaert and Beer Kitano, 1994]. The main idea of this approach is to encode rules that will themselves self-organize to produce a phenotype, as is the case with biological morphogenesis. However, the biological understanding of morphogenesis was inspired by concepts of ''Mechanics of Development'' that have been worked out in experimental embryology in the first half of our century. The biological conception of morphogenesis includes, apart from the idea of self-organization, so-called ''regulation'' principles. Biological morphogenesis, as a distinct self-organizing processes, requires effective non-linear feedback between its dynamic components [Beloussov et al., 1994]. This feedback should, on one hand, rapidly and precisely trace the deformation of embryonic layers caused by active mechano-chemical processes and, on the other hand, affect these very processes.
It is the approach of coupling a morphogen to geometrical changes, and having the geometrical changes in turn give rise to a change in the morphogen pattern, and so on, which is employed here, as an extension of the same approach of previous works [Spirov ,1992; ,1993a, ,1993b; Cummings ,1990; ,1994]. According to Harrison ,1981, morphogenesis is the creation of a complicated shape out of a simpler one by chemical processes in living organisms. The essence of it is symmetry-breaking. The early embryos of many species undergo form changes almost entirely by expansion and folding of a simple epithelium (Cf. Fig.1). Let us overview schematically the changes in symmetry considering as an example the morphogenesis of sea urchin embryo from the blastula stage. By the symmetry criteria this period of development could be subdivided into the following stages [Beloussov, 1987]:
In this article we will pay attention on the mechanisms of decreasing of symmetry order (desymmetrization) from m*µ symmetry to 1*µ one.
Recently we [Spirov and Boinovich, 1992; Spirov, 1993a, 1993b] had analyzed a system of Turing-like equations coupled to geometric changes, where these geometric changes in turn couple back to alter Turing diffusion coefficients of morphogens. In other words, I use known idea of coupling of one pattern to the formation of another. Development of sea urchins was analyzed using this approach. I briefly review the main results of previous works including axis tilting bifurcation as the case of symmetry breaking via secondary bifurcations. Particularly, a very simple algorithm of making of secondary bifurcations results in transition from initial unipolar gradient pattern to bipolar pattern with axis tilting.
Then we describe one more and a new case of bifurcation in the reaction-diffusion system when we gradually decrease concentrations of reactants and thus achieve transition from continual description by PDEs to stochastic simulation of a few particle ensemble. My current work aims at analysis and simulation of expression patterns of gene-controllers of morphogenesis. Expression pattern of multiple early activated genes predetermines the ensuing processes of differentiation and morphogenesis in early development. Geometrically regular patterns of gene expression (7- and 14-stripped patterns along the Drosophila early embryo or 4- and 8-radial patterns in Drosophila imaginal discs) vividly bring to mind well-known examples of patterns appearing in reaction-diffusion systems far from equilibrium. Activation mechanisms of Drosophila segmentation genes and sea urchin early activated genes have been well investigated. These regulatory genes form functional networks in which each gene acts positively or negatively on other ''netters'', and vice versa. Regulatory peptides interact with one another as well as with their target DNA sequences in accordance with non-linear kinetics. These interactions could be described from a synergetics viewpoint.
However, one must take into consideration the fact that, apart from small reactant molecules, such as Belousov-Zhabotinsky reactants, in the expression patterning there participate large slow-diffusing regulatory peptides, which are present in a few copies per cell/nucleus. It is quite evident that ODE or PDE are inadequate for description of these molecules behavior. On the contrary, one could try to take advantage of discrete calculations of the stochastic appearance, binding, elimination and dimerization events in the gene ensemble. The processes of gene regulatory elements interaction with their targets are essentially non-linear and could give, as a result, a Turing-like behavior of the system. To my surprise, the dynamics of the model do not display classical pattern-formation behavior, instead it shows a quasi-regular near-chaotic one. Namely, regular patterns are permanently spontaneously disturbed and time and again partially restored. What is more, wave number of the regular pattern is not constant for a given parameter set, but fluctuates around a given value. Coupling such gene expression pattern with the morphogenetic movements, with ensuing feedback from form to pattern, could give remarkable ''monsters''!
I hope that my results will contribute to understanding of mechanisms of morphogenesis, both in its own rights and as an approach to artificial morphogenesis, such as development of Dellaert and Beer's autonomous agents [Dellaert and Beer, 1994; 1994].
Although a large literature exists for equations which specify fields of values in the plane with specified boundary values, or sphere, little or no literature exists for the case where the ''morphogen field'' interacts with the surface to change its shape, and the field in turn is itself changed because of the surface changes, and so on. While considering shape changes it is important to take into account both mechanical forces and the chemical kinetics, and their both equally deserving of inclusion in the differential equations. However, in the pattern-form interplay model we explore the possibility that the secondary role of mechanics can be represented algorithmically [Spirov and Boinovich,n1985; Spirov1992; 1993a, 1993b; Cummings, 1985; 1989; 1990; 1994; Harrison and Kolar, 1988].
Equations for morphogens All Turing-like models require two diffusing substances as a minimum, [X] comparatively slow-diffusing one and [Y] that diffuse much faster [Lacalli and Harrison ,1991]. We use here, following other authors [Harrison and Kolar ,1988; Harrison et al. ,1988], the Brusselator as a system that has been extensively studied in relation to chemical pattern formation, as well as dual Brusselator as system with perfect interpretation in molecular biology terms [[Lacalli ,1990]. Namely, assuming that the morphogens involved in gradient formation are primary gene products and not metabolites, the main steps in the reaction scheme leading to X and Y formation must represent some combination of gene transcription processes. This implies considerable complexity of regulatory control. The model specifically requires the presence of multiple inputs, including the gene self-activation by products [Lacalli ,1990].
We consider the application of these ideas to the object-oriented modelling of specific morphogenetic processes such as gastrulation of sea urchins. Initially the model describes geometry of a spherical layer. Each cell produces and exchanges the morphogens X(s) and Y(s) in conformity with Brusselator or dual Brusselator model. The set of parabolic equations is solved by the finite difference method. Steps in computation of the morphogen distribution must alternated with steps in which the new morphogen distribution is used to govern morphogenetic movements. At odd numbered steps, numerical integration of the equations was carried out until a steady state was reached. At even numbered steps, ''translation'' of new patterns into new forms occurs by means of ''morphogenetic movements''. The reaction-diffusion pattern continually reorganizes itself in response to the shape change of the simulated object and this change occurs because of the existence of the pattern (Cf. [Harrison and Kolar ,1988]).
According to the model morphogen-induced morphogenetic movements are somewhat separated in time. It should be stressed that the morphogen pattern develops first, followed by the appropriate morphogenetic movement (geometric change). This feedback loop from the morphogen patterns to changes in surface geometry is determined by cell form changes (namely columnarization of cells and/or cell apex constriction) which are dependent on X-concentration. Fred Cummings [1989; 1990; 1994] has been studied elementary expressions for the gauss curvature K in terms of the parameters s, the ratio of local basal to apical cell surface area, and h, the local sheet thickness. The problem at hand is to relate the radii of curvature to s and h, and thus to K, which is related to R1 and R2 by K = 1/ (R1*R2). Elementary solution of this task, according to Cummings, gives

Thus, empirical knowledge of the dependence of s and h on the morphogen m will determine the gauss curvature at each point on the surface. It seems reasonable to presume, for example, [Cummings, 1994], that both of these functions s(m) and $h(m)$ are monotone functions of m, perhaps even the ''S''-shaped functions, which often are used for description of biological processes. In the model we assume that s(m) is ''S''-shaped function of m.
It seems that morphogenesis is based on interactions between the genome inside each cell nucleus and the ''environment'' of neighborhood cells of the multicellular layer. Cells are thought can test its local (bio)mechanical environment by sensing local changes in the layer geometry [Bjorklund and Gordon ,1993]. In this way the organism acquires the required cells, in the right place, and at the right time. A simplest and effective mechanism of local cell respond to completion of appropriate morphogenetic movement consists in differentiation of intercellular contacts. In this case the feedback loop from the surface geometry to morphogen pattern is determined by the change in cell-to-cell conductivity (proportionally to local curvature in that part of the cell layer, wherein the morphogenetic movements have occurred). The above discussed rules of pattern and form interactions are described by following general set of equations:
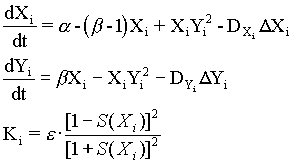 (2)
(2)
Xi and Yi are concentrations of intermediates of the Brusselator in the i-cell; a and b are parameters; DXi and DYi are position-dependent diffusion coefficients; Ki is local gauss curvature (in vicinity of the i-cell); e is parameter; S(Xi) is "S"-shaped function of Xi. (See Eq.1). In my previous work [Spirov, 1993] I used such simple algorithm for 3D graphic realisation of local gauss curvature dependence on local morphogen concentration. Translation of the X gradient in the areas where X > Xcr. was carried out by means of morphogenetic movement in accordance with formula:
![]() (3)
(3)
where R(tn) is the radius-vector of the inner surface of the model at the stage tn (present stage), R(tn-1) is the radius-vector of the surface at a previous stage, q is empirical parameter.
In the same paper I used following expression for diffusion coefficients Dj as function of the local gauss curvature or the local increment of the radius-vector R of the surface which, in turn, is a function of X:
![]() (4)
(4)
DJt1 is a local diffusion coefficient at the recent stage t1, DJt2 is a local diffusion coefficient at the previous stage t0, p is empirical coefficient.
In case of more refined modelling, depicted in Fig.1, the program was tested with more precision iterative procedures for approximation of radius-vector (gauss curvature) dependence on X, but qualitative behavior of the model is turned to be insensitive to peculiarities of algorithms. The symmetry breaking: axis tilting phenomenon Carrying out a number of computer experiments with the model reveal that it behavior is similar to early stages of sea urchin morphogenesis [Spirov, 1993]. The model simulates flattening of a blastula bottom, invagination, elongation and subsequent morphological metamerization (''chambering'') of a ''gut'' with maintenance of an initial axial symmetry (an animal-vegetal axis), as well as determination and invagination of an ''orus'' (i.e. determination of a second axis of symmetry: an oral-aboral axis).
A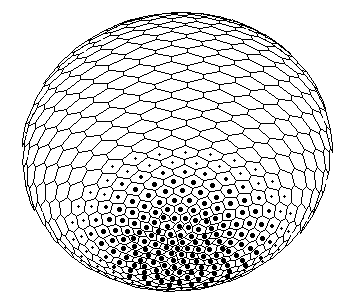 B
B C
C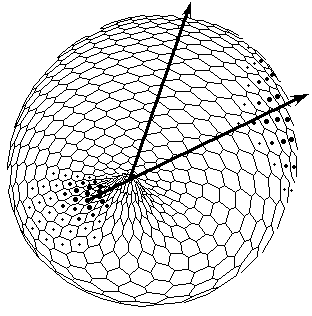 D
D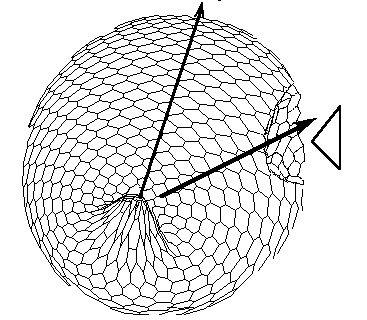
Figure 1. The axis tilting phenomenon in the Pattern-Form Interplay Model. Values of parameters of the Brusselator are a =3; b =15; initial values of transport coefficients are D0X=110; D0Y=30; boundary conditions are XNorth pole=7.0; XSouth pole=0.0; dYNorth pole/dt=0.0; dYSouth pole/dt=0.0. A front wall of the model figures are removed in all pictures.
A. An initial state of the model with spontaneously generated concentration gradient (for Brusselator RD system) with maximum at the ''South'' pole and minimum at the ''North'' pole of the spherical multicellular layer. The more are 'nuclei' inside a cell, the more are local concentrations of one of the Brusselator intermediates [X].
B. Simulation of invagination and formation of gastrula. Form of the model (perspective projection) after ''translation'' of the X-gradient on Fig.A according to iteration algorithm for solving the Eq.(1).
C. Bipolar pattern as steady state established in Brusselator RD system with position-dependent diffusion coefficients.
The one pattern (Fig.A) is coupled to the formation of the other. New pattern differs not only in overall geometry but also in tilting of the axis as compared with initial gradient. D. Form of the model (perspective projection) after translation of the secondary bipolar gradient on the Fig.C. We achieved the initiation of invagination of ''orus'' (indicated by large arrow head). In the case of determination of the second axis of symmetry and the invagination not only of a ''gut'', but also of an ''orus'' was established (Fig.1). Thus we achieve such biologically essential case of symmetry breaking (from m*µ symmetry to 1*µ one) via axis tilting.
This symmetry breaking as a consequence of secondary bifurcations is the main subject of interest in remaining part of the paper.
We know that the response of gene regulatory elements, which involves the mobilization of transcription machinery, is a highly cooperative, non-linear phenomenon. In principle, these elements could respond sharply to very small concentration differences. However, such highly non-linear concentration-reading device is effectively trying to assign a value to a limited sample of molecular events, whose distribution in time contains an inherent random component arising from the stochastic nature of molecular motion (for details See Lacalli and Harrison ,1991). The standard deviation for this distribution is equal to the square root of the number of binding events by molecules to DNA. If a given binding site is to measure concentration to an accuracy of 1* 10-4 molecules must be sampled [Lacalli and Harrison ,1991].
However, one must take into consideration the fact, that large slow-diffusing peptides-regulators participate in expression patterning in a few copies per cell/nucleus. For example, regulatory domain of one of two alleles of the sea urchin cytoskeletal actin gene contains about 20 sites for 13 different regulatory peptides. By means of in vivo competitive titration experiments [Davidson ,1989] it have been found that the number of these peptides per nucleus range from 500 to 1100 copies!
It is quite evident that such amount is inadequate to use ODE or PDE for its description. But anyway, these particles interact with one another and with their targets in chromatin in accordance with non-linear kinetics, which could be described from the point of view of synergetics. On the other hand, one could try to take advantage of discrete calculations of stochastic appearance, binding, elimination and dimerization events in the processes of gene regulation. Hence, if we have one gene with, say, 12 targeting sites in a DNA regulatory element for 4 different regulatory peptides, each present in 100-1000 copies per cell, then we must really simulate the discrete state changes of this gene regulatory element. This approach, apart from evident proximity to molecular biology reality, would be useful for estimation of features of a few interacting elements system with non-linear kinetics as compared with ODE/PDE approximations.
Our simulations by discrete computation approach show that multicellular layers with a few elements ensemble inside each cell can exhibit self-organization phenomena similar to RD approach. I execute computer simulation of this gene net activation both in spatially one-dimensional (Fig.2) and in two-dimensional (Fig.3) cases. The model describes changes in state of gene regulatory elements as consequence of binding/elimination, dimerization/dissociation and competition for targeting sites of site-specific transcription factors. String variables describe localization, strength of binding and mode of action of bound ''factor'' for each simulated gene regulatory region at each step of the calculation. Transcription/translation level (and, hence, probability of collision with given gene product) depends upon number and balance between bound activators and repressors.
To make spatially distributed model, we must take into consideration exchange of transcription factor molecules between given nucleus and its neighbors. We take into consideration also that cytoplasm (and nucleus, possibly) is capable of the proteins degradation.
Let us consider following X-Y gene pair. Assume that X-response element in Y promoter region consists of one cluster of high affinity target sites (for X proteins) and another cluster of low affinity target sites (for X proteins, also). We assume that high affinity sites bind X proteins as activators, whereas binding of the X protein to low affinity sites represses X transcription. In addition, we assume that low affinity sites overlap with Y [autoregulation] binding sites. As a result, X and Y proteins compete for specific binding in the Y promoter element. Assume also that X promoter element has at least one cluster for Y proteins binding as activators. In accordance with multimerization model, let's assume that X protein can bind to these target sites also as a dimer which can not to activate X gene. As we can see, this X-Y pair has two stable states:
As we discussed above, the production of X and Y proteins in each nucleus depends upon state of the Y and X promoters, i.e. upon proportion between occupied activation and repression sites. We assume that the ability to activate transcription depends on the square power of activator concentration. At each round of X (and Y) transcription, the state of the promoter element can change, depending upon consequences of stochastic collisions of X and Y proteins with target sites, elimination of the proteins out of target sites, etc.
A
B
Figure 2. Computer simulation of appearance and maintenance of spatially periodic pattern of a gene expression along a row of 50 cells. Bars presents ''intracellular'' concentration of product of X-gene. A. An example of one of the X-patterns. B. Dynamics of the X-pattern from 1 to 150 time step. In this case each pattern, like at (A), is stretched to 5-pixel high image and all 150 images is arranged in a ''rouleau''.
Intuitively it is clear, that, in accordance with the model assumptions, X/Y pattern being two partly shifted series of bands, must be stable. In the bands of high Y production practically the X transcription is completely repressed (and vice versa), but high level of the Y gene activation is supported by diffusion of X\ protein from neighbor X bands (and vice versa). Numerical experiments with the model really reveal spatially periodic states (Fig.2A). Wave number is depended, first of all, on X and Y transport coefficients.
However, it is not a stable N-wave pattern, on the contrary it is a sort of oscillation around ideal steady state (Fig. 2B). This simple example of the one-dimensional pattern dynamics presents features of the near-regular quasi-chaotic behavior. Meanwhile we can find 3-, 4- and upto 6-wave cases! We can see that the system ''move around'' the 5-wave steady pattern. In other words, ''ideal'' 5-wave pattern is permanently disturbed and time and again restored.
A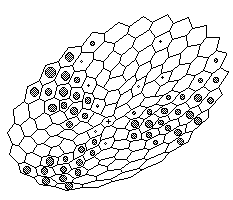 B
B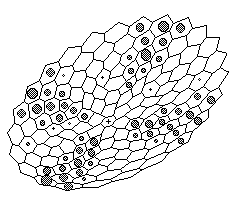
Figure 3. Computer simulation of appearance and maintenance of radial pattern of gene expression in case of two-dimensional radial symmetric layer (perspective projection) . The more grey 'nucleus' inside a cell the more local concentration of the X-product. Spatially two-dimensional case simulates spheric cell layer. We assume radial symmetry of cell arrangement for facilitation of appearance and maintenance of radial patterns.
Sustained patterns strikingly remind known examples of gene expression patterns in imaginal discs, particularly hairy-achaete gene pair expression. In this two-dimensional case we also can see not stable pattern but quasi periodic oscillations around three-, four-, five-fold patterns (Fig.3) and chaotic patterns (not shown at the figure).
Bifurcation in nonlinear PDEs is a well-known mechanism for spontaneous pattern formation. Autocatalytic reaction-diffusion systems have been shown to undergo such bifurcations, and stable inhomogeneous concentration patterns arise (Turing structures). Such systems have been studied extensively both analytically and numerically as they may play an important role in spontaneous biological pattern formation. The tilting of initial gradient to secondary ''oral'' axis which we found for closed layers reminds recent results of [Hunding ,1987; Hunding and Brons ,1990].
Axel Hunding numerically and analytically investigated secondary bifurcation points for three-dimensional spherical reaction-diffusion system, when initial symmetry is broken by making diffusion- and rate-coefficients functions of primary gradient. It is well-established that one of the concentration patterns which has been shown to arise in RD-systems in a spherical region, is a gradient pattern, with high concentration at one spontaneously generated pole, and low concentration at the opposite pole of the sphere. It has been argued by many authors, that such a pattern might be the pattern governing the formation of animal-vegetal (''north'' and ''south'') poles in the developing egg. It was assumed, that this steady concentration gradient affects the parameters in a second, otherwise independent, Turing-like system (namely, Selkov model) [Hunding ,1987].
It was shown, that such a very simple modification of the basic Turing-type RD equations results in bipolar patterns having orthogonal orientation with respect to initial polarity of the system. Hunding's result that the emergence of the perpendicularly oriented bipolar pattern obtains in a broad class of chemical reaction systems is an important general result for understanding of early morphogenesis. They explain the emergence of a bipolar order orthogonal to the animal-vegetal axis in the cleaving egg. As is the case of Hunding ,1987 numerical simulations in three dimensions, my numerical simulations in two dimensions of a closed axis-symmetrical surface show the axis tilting phenomenon. Thus the axis tilting bifurcation may be introduced by coupling of the initial gradient to the second Turing-like system both in a sphere (cleaving egg model) and in a closed surface (gastrula model).
However, in my calculations, a new axis was not orthogonal to initial one (Fig.1). Secondary axis establishment is one of the mysteries of developmental biology and I hope that my computational results could help to reveal it.
Amongst modern and fossil mutant forms of invertebrates we can find amazing cases of mis-regulation of body plan radial symmetry. For example, offspring of the same individual mutant of sea urchin can have three-, four- or five-fold symmetry of body plan (Fig.4). These intriguing cases of developmental mis-regulations vividly recall our near-chaotic behavior of gene ensembles.
A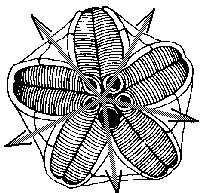
B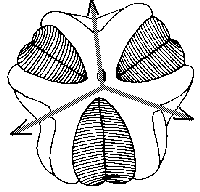 C
C
Figure 4. Hinegardners's square mutant of sea urchin with deregulation of mechanism of determination of embryo symmetry (According to Raff and Kaufman[1983]).
A. Normal penta-radial larva.
B,C. Mutant larvae.
In my model and, I think, in living systems such spontaneous disturbances of the symmetry are internal to the system as is the case of chaotic behavior of reaction-diffusion system. It is quasi-chaos around steady pattern. In living creatures this behavior appear as the result of some mutations. At any given moment pattern of the gene expression, as a snapshot from the screen, may display three-, four- our five-fold symmetry. Assume, in accordance with developmental program, that in fixed moment of developmental time the achieved 3-, 4- or 5-fold symmetry of the gene-controllers pattern will be used as the prepattern for following morphogenesis movements. Since that the gene expression dynamics became frozen by switching off the expression control mechanism. As a result, since this stage, the following morphogenesis proceeds in accordance with 3- or 4- or 5-ray (fold) symmetry. The choice depends on chance!
Hence we achieve the model behavior demonstrating the above mentioned experimental and fossil data when genetically identical offspring of the same mutant develop in accordance with both normal and new cases of the body plan symmetry. If one of a new body plans becomes selectively advantageous comparing to normal one, then next new mutation could fix a novel advantageous morphogenesis prepattern. Hence such genetic events could give new ''hopeful monsters''. As a consequence, this could lead to appearance of species-ancestor of a new taxa! In this overview, we would point out that chaos is relevant to the emergence and maintenance of complex behavior in frame of the pattern-form interplay models.
Supported by Russian Foundation for Basic Researches (Grants No 96-04-49349 and No 96-04-49350). The author wishes to thank Chrystopher Nehaniv and Maria Samsonova for helpful coments and critical reading of the MS.
This page hosted by ![]() Get your own Free Homepage
Get your own Free Homepage