Genes, Morphogenesis, Evolution: Life and ALife Aspects

Models with diffusion (Class1 models)

Here we represent the application of principles of autocatalysis and lateral inhibition to biochemical reactions with diffusion.
Let us consider a substance a, called as activator, which stimulates its own production (autocatalysis) and the production of its antagonist i, named as inhibitor. To carry out the necessary long-range inhibition, the inhibitor must diffuse more rapidly.
In an extended field of cells a homogeneous distribution of these substances is unstable, since any small local elevation of the activator concentration - resulting perhaps from random fluctuations - will be amplified by the activator autocatalysis. The inhibitor which is produced in response to the increase in activator production, cannot halt the locally increased activator production, since it diffuses quickly into the surrounding tissue and suppresses activator production outside the activated centre. Thus, the locally increased activator concentration will increase further, with increasing concentration, the maximum becomes narrower and narrower until some limiting factor comes into play, for instance, the loss of activator from the narrow peak by diffusion become sequel to the net production.
A stable activator and inhibitor profile is ultimately obtained, although both the substances continue to be made, to diffuse, and to be broken down. Such a simple system of two interacting substances is, therefore, able to produce a stable, strongly patterned distribution from a nearly homogeneous initial distribution, as it occurs in biological pattern formation.
The general representation of such a system is:

The first term in the right part represents the diffusion process, where D_a and D_i are diffusion constants for a and i correspondingly; the second term represents other processes such as production and decay, they may be written as

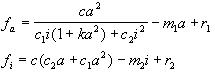
here if c₁=0, then c₂=1 and vice versa.
In this equations production is represented by the first and third terms, second term represents the decay.
One of the most known and frequently used type of the systems of such a kind can be derived if to set c₁=1 (correspondingly c₂=0), k=r₁=r₂=0, namely

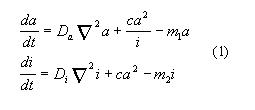
Resulting distribution may be monotonous or periodical and changes as a function of parameters. The pattern formed inthis way may be stable or oscillating with the time. The positioning of high concentrations is produced by small internal or external asymmetries or by local disturbance.
This local high concentration can serve as signaling system, for instance to initiate head formation in hydra. A pattern formed in this way has strong self-regulatory properties.
Let us also to consider a special case of such a systems with feedback loop.
To do this would require to set c₂=0, then

The small basic (activator-independent) activator production r₁ can initiate the autocatalysis in areas of low activator concentration. As we will see, this term is important if new centres have to arise during growth or regeneration. In contrast, the basic inhibitor production can suppress the appearance of secondary maxima, a feature which is important if an ordered sequence of structures is to be specified by positional information. If the activator production saturates at a high concentration due to term 1/(1+k*a*a), the activated area is self-regulated.

Other molecular realization of autocatalysis and lateral inhibition principle may be, for instance, the processes in which inhibition effect is realized by depletion of a substrate consumed in autocatalysis. From mathematical point ofview this means that

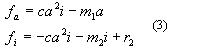
Also one has to remember here well-known in developmental biology Sel'kov's model:

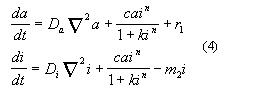
where n is known as Hill's number.
In this model one assumes that the activator reproduction is compensated by selfregulated reproduction of the inhibitor. The stable pattern formation is also possible in this case.

This page hosted by Get your own Free Homepage