


We may be considering the space of all possible length sequences of DNA composed of four types of bases. Our genotypes consist of set of N sequences of length L, forming a certain region in the sequence space. The majority of possible sequences are forbidden in biological reality, leaving only a subset of N allowed ones for participation in the evolution.
Let us include in consideration a mutation that takes place in a sequence. To measure the strength of the change we can use a metric on the sequence space introduced, say, by means of the Hamming prescription. The Hamming distance between two sequences is defined as the number of non-coincidences. Two sequences with Hamming distance equal to one are neighbours.
Discussing the problem of the complexification of living beings we really bringing in mind following picture. Neighbourhood structure of the sequence space of ancestor and its advanced offspring are generally two unconnected graphs, as is the case of Fig.a. Evolutionary pathway from lower to higher level of organisation needs connection between the graphs. It is impossible to jump from real ancestor to potential offspring graph. All possible sequences formally connecting two graphs are forbidden because they give abnormal phenotypes.
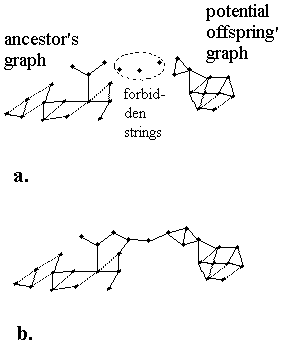
Apparently to achieve the higher level, the evolutionary process must have chance to get over the gap. In principle, we can imagine some ways to achieve this. The simplest one consists in decreasing of adaptive role of the traits under consideration. This leads to broadening of variability the traits. In such a case, previously forbidden sequences determining phenotypes with deviations will get chance for reproduction. As a result, connection between actual and potential graph forms, as in the case of Fig.b.
Complicated topology of the neighbourhood structure of the sequence space (Fig.a) is ensured by intrinsic potential for complexification of the string regulatory networks, while connections between isolated actual and potential graphs might be facilitated by the robustness of the developmental mechanisms. More generally, appearance of such connections between diverged levels of organisation is achieved not exclusively by broadening of variability of the traits but also via exploitation of the canalization schemes of development.
Complexification of Regulatory Nets
See also