Nowadays morphogenesis becomes commonly used term in some interdisciplinary fields. This term reflects general idea of structure formation governed (directly or indirectly) by sets of rules or algorithms. However, biological meaning of morphogenesis had inspiring by concepts of "Mechanics of Development" that have been working out in experimental embryology to the first half of our century. The biological morphogenesis conception includes, apart from self-organization idea, so called "regulation" principles. By regulation biologists mean the ability of developing organisms to regulate their pattern to their size. Apparently it is one of the most striking properties of living organisms. Two sides of holistic idea of regulation preferably worked out in modern theoretical biology. It is modeling of regeneration (i) and size invariance of the morphogenesis models (ii). The significance of these theoretical findings for neighbor scientific fields, including artificial life, is self-evident. Imagine, for instance, such a robot which after "cutting" on two parts, instead of full damage, each part of it will reorganize itself in such a way that two smaller but functionally complete robots will appear. Or imagine computer program, which while partly damaged will regenerate and repair erased blocks.
In modern theoretical biology literature we can find strict but elementary models of regulation which appropriate to use in ALife. Simplest tutorial bases on well-known idea of developmental gradients. Fred Cummings proposes "Laplace algorithm" for the purposes of formal description of regulating development (1985; 1994). According to Laplace algorithm, the value of gradient (chemical concentration in case of morphogen gradient) at one point in space is the average of the value at of that same quantity at all equidistant points. The Laplace algorithm size regulates since it contains no mention of size or scale.
Following Fred Cummings (1994), consider a "worm" of length L, and with fixed values 10 at one end and 1 at the other, as in (10-9-8-7-6-5-4-3-2-1). Next imagine cutting out a section of the worm, say, the values 7 through 4, and joining the 8 to the 3, to form a worm of about half the length of the original. Just after "surgical intervention" the worm contains the values of (10-9-8_3-2-1) in this order along the line, where 10 and 1 are fixed. Two possibilities ensure, depending on whether the worm can regenerate by adding new "cells" by cell division, or by adding no new elements, only re-valuing the existing cells. Clearly, the 8 and 3 do not satisfy the Laplace algorithm after joining them, and are not the average of their neighbors. First consider the case when no new cells is added, but the existing cells take on new values in successive stages to satisfy the algorithm as best as possible at that moment. This will continue recursively until a steady state is reached where all values take on the average of their neighbors. Then the length of the finally regenerated worm will remain about half of its pre-excision length, but the values will go from 10 down to 1 as before. Then we have: (10-9-8-3-2-1) (10-9-6-5-2-1) (10-8-7-6-3-1) (10-8-6-4-2-1) … Finally we achieve regulation as size invariance with desired degree of accuracy all along the creature length.
Next consider the case of a Cummings' worm that regenerates via cell division. In this case the values 10, 9, 8, 3, 2, 1 are all fixed, but obviously the Laplace algorithm is again not satisfied with an 8 adjacent to a 3. This organism now uses the strategy of cell division at the juncture between the 8 and 3. As a result, the new cell is now assigned the value 11/2 = (8+3)/2, so that it now appears as (10-9-8-11/2-3-2-1). This is, of course, an improvement, but still the algorithm is not satisfied, for the 8 and 3 are still not the average of their neighbors. Cell division in the second time-step occurs between the 11/2 and 3, as well as between the 8 and 11/2. These two new cells are assigned the average of the neighbors, namely 17/4 and 27/4, respectively. This process of cell division continues until the worm has satisfied the Laplace algorithm and has regained its original length, as well as its original pattern of values. Hence, we achieve complete regeneration of the creature.
In frames of developmental gradients ideology, all upper levels of an organization are predetermined by local developmental gradient values. If developmental gradient begins to rebuild, then overall structure undergoes reorganization. We sketched one-dimensional examples, but apparently this is straightforwardly extendible to the situation in two, or three dimensions. Word description of the models allows elementary simulations in frame of cell automates approach, especially the algorithms would be suitable for simulated evolution of the Dellaert & Beer's developing autonomous agents (1994a;b; 1996).
Of course, it was oversimplified tutorial example. However, a vast word
of regulative models comes to light in the field of epithelial morphogenesis.
Fred Cummings, simply starting from the extremum formulation of the Laplace
algorithm for the multicellular layer morphogenesis (as in the case of
Fig.3) with a necessary constraint, was lead to following non-linear equation
for morphogenesis. In conformal coordinates u
and v this equation has form:
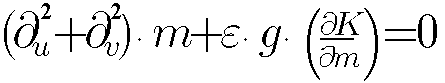, where K
is Gauss curvature of the epithelial layer, m
is local morphogen concentration, g
is metric function and e is parameter.
The term 
act as a self-source
term in this Poisson-like equation. This interesting equation turned to
exhibit size invariance as a very natural consequence, almost as a sort
of side benefit, and not as a contrived effect. As Cummings (1990) wrote,
it is apparent that it will be difficult to think of another way in which
the size invariance could occur.
Get your own Free Homepage