Alexander V. Spirov
ABSTRACT
Presented model is aimed at simulation of regulatory gene networks role in "orchestration" of morphogenetic movements in developing embryos. Three constituent parts of entity developmental process are taken into consideration. It is dynamics of expression of the regulatory gene network (i), processes of physiological gradients formation (ii), and form changes in developing embryo (iii). The characteristic feature of the model is feedback loops between the processes in regulatory gene network, biochemical pattern formation and embryo form changes. The model is directed towards prediction of coupled changes of the gene expression patterns, the embryo surface geometry and biochemical/physiological pattern. Potentiality of approach is demonstrated by simulation of gastrulation and following morphogenesis of sea urchin embryo. Computer experiments with the model reveal behavior that simulates the processes of invagination with subsequent elongation and then metamerization of a "gut", followed by determination of "oral field" and the beginning phase of "orus" formation.
INTRODUCTION
Genes regulating complex integrated functions, such as the programming of early development, often encode proteins with multiple conserved domains (such as HOX genes, zinc-finger and leucine-zipper genes). These genes are thought to integrate into functional networks that evolved by duplication of small number of primordial genes. The resulting superfamilies of genes form structural and functional networks. In vertebrate the four HOX gene clusters are a highly conserved group of genes evolutionary related to the insect's HOM complex (Holland 1992). Extensive analyses of the patterns of gene expression for members from HOM and HOX clusters show that domains of gene expression are spatially restricted in different embryonic sites and axes. An important feature of these complexes is linear correlation between the position of the gene in HOX cluster and its relative axial domain of expression in many embryonic tissues (De Robertis et al. 1991). This property is termed collinearity (Lewis 1978), and is conserved in arthropods and vertebrates. The HOX genes are believed to function in the specification and interpretation of positional information in the embryo through the particular combination of genes (HOX code).
Computer model presented in this paper is aimed at simulation of regulatory gene networks role in "orchestration" of morphogenetic movements in developing embryos. Three constituent parts of entity developmental process is taken into consideration. It is dynamics of expression of the regulatory gene network (i), processes of physiological gradients formation (ii), and form changes in developing embryo (iii). The characteristic feature of the model is feedback loops between the processes in regulatory gene network, biochemical pattern formation and embryo form changes. In the model, formation of biochemical/physiological gradients causes subsequent morphogenetic movements. In its turn, the geometrical transformation of the model disturbs its biochemical pattern and a new pattern appears. In turn, a new pattern causes further morphogenetic movements. And so it occurs up to the achievement of the equilibrium between the geometry of the model and the distribution of morphogens in it. But all steps of the processes of physiological gradients/morphogenetic movements interactions are under control of regulatory gene network. The spatio-temporal pattern of the regulatory genes expression serves as a map or scheme of spatially and temporally local initiations of instabilities in pattern-form interactions. In other words, gene expression pattern "says" when and where pattern-form instabilities must be appeared.
MORPHOGENESIS GUIDED BY GENETIC NETWORK ACTIVITY
We consider the application of these reasons to the modeling of specific morphogenetic processes such as gastrulation of sea urchin embryos.
Modeling of Spatio-Temporal Expression Pattern of Gene Nets.
It is established by many authors that genes-regulators of morphogenesis and differentiation (such as HOX genes, zinc-finger and leucine-zipper genes, and so on) have extended promoter regions with up to tens target sites for binding of specific transcription factors (HOX proteins, Zn-finger and leucine-zipper proteins, etc). Multiple copies of protein recognition sites are thought to act synergistically, presumably due to some functional cooperativity of the regulatory protein involved. This cooperativity presumably yields sharp gene activation thresholds (Small et al. 1991). It is known that two-fold difference in bcd-protein (specific morphogen for Drosophila embryo) concentration appears sufficient to distinguish between ON and OFF states of expression of sensitive genes.
One can describe each such regulatory gene extended promoter with transcription factor molecules as kind of synergetic system (say, as Brusselator or Turing system). In the model the extended promoter region with multiple target sites is described as tandem consequence of "single-seater" target sites. There are several classes of sites and several site-specific transcription factors (TF). Initially all sites are free. Time by time one molecule of TF randomly hits to one of the sites. Different kinds of TF appear with different but predetermined probability. Whether TF-molecule binds or not and the affinity of the binding depends upon specificity of the site and upon state of neighbor sites. Depending upon concrete set of algorithm and parameters, the computer model demonstrate concentration-dependent sharp threshold between ON & OFF states of the gene, chaotic dynamics of the network expression, and complicated spatio-temporal patterns of the network expression.
Pattern-Form Interaction Modeling
Pattern-form interactive part of the model presented has following organization (see Spirov 1992; 1993). Initially the model has geometry of a spherical surface with geodesic grid, with "cells" arranged according to symmetry of radial cleavage. The total number of cells in the grid is close to the number of cells when gastrulation of echinoderms begins. Each cell produces and exchanges the morphogens X and Y in conformity with Brusselator model. We use here, following other authors (Harrison and Kolar 1988), the Brusselator as a system that has been extensively studied on chemical pattern formation. The set of parabolic equations is solved by the finite difference method.
Under certain initial conductivity of cell-to-cell communications the trivial homogeneous distribution of morphogens is unsteady.
The sequence of events in the model is subdivided into stages. On the first and following odd numbered stages numerical integration of the equations was carried out until a steady state was reached. On the second and following even numbered stages "translation" of new patterns into new forms occurs by means of "morphogenetic movements". This feedback loop from the patterns of morphogens to changes of surface geometry is determined by flattening of cells (thickness of height of cells), wherein the morphogen X concentrations are above critical.
Really, endoderm cells of sea urchin early gastrula undergoes polarized stage-specific changes in shape and motility: they flatten markedly along their apical-basal axis. Supposedly, in the evolving object the dependence of the local curvature K of the surface on the local morphogen concentration X is determined by a simple function: K=K(X2). The bases of such form of functional dependence were presented by Cummings (Cummings 1990).
An effective mechanism of reinforcement of pattern-form interaction consists in differentiation of intercellular contacts in the regions of the embryo marked by specific pattern of regulatory genes expression (where the morphogenetic movements took place on previous stage). In this case the feedback loop from the surface geometry to morphogen patterns is determined by change of the cell-to-cell conductivity in that part of the cell layer marked by the expression of some members of the gene network. In the model we use an idea of coupling one pattern to the formation of another according to Hunding's version (Hunding, 1987). This approach consists of imposing in the Turing-like system of pattern formation the gradient of a key parameter that controls the appearance of pattern allowed by the other parameters of the system. In our case it is natural to use as the key parameter the coefficient of cell-to-cell communication conductivity, since this is in a close agreement with known data about development of the system of cell-to-cell communications in sea urchin gastrula.
A B
B C
C D
D E
E F
F
FIGURE 1. COMPUTER SIMULATION OF EARLY DEVELOPMENT
OF SEA URCHIN EMBRYO.
Carrying out a number of computer experiments with the model reveals
behavior of the model similar to early stages of sea urchin morphogenesis.
Model dynamics simulate flattening of a blastula bottom, invagination,
elongation and since then a morphological metamerization ("chambering")
of a "gut" with maintenance of an initial axial symmetry (an
animal-vegetal axis) followed by determination and invagination of an "orus"
(i.e. with determination of a second axis of symmetry (an oral-aboral axis))
[Figure 1]. There is possibility for modeling of abnormal early development
such as exagastrulation in sea urchin embryo [Figure 2].
A B
B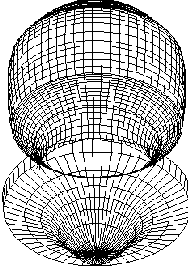
FIGURE 2. SIMULATION OF EXAGASTRULATION IN SEA URCHIN
EMBRYO.
DISCUSSION
Why is position in embryo specified in a complex combinatorial manner while the products of one or two co-ordinate genes, distributed in a concentration gradient along the embryo axes appears to fulfill the same requirement in a simpler way? One can propose the following considerations as a plausible explanation (see Baumgartner and Noll 1990). A gradient contains positional information in an analogue code. On the other hand, the combinatorial activity of regulatory genes could specify position in a digital code. Analogue information is less stable and hence more error-prone. Therefore, if position needs to be specified more stable, it is important to convert the initial analogue positional information into a digital form. This conversion of analogue to digital positional information appears to be mediated by gene networks under discussion.
Let us consider, in conclusion, the question of size invariance of dynamical models of morphogenesis. One of the striking aspects of living organisms is the size invariance. A further condition on any algorithm (and a powerful one) is that it be "covariant" (in geometrical sense). This means that it must give the same "field" of morphogen for any choice of coordinates. For example, since the Gauss curvature is an invariant - a scalar - it is the prime candidate to enter the algorithm (Cummings 1985, 1989, 1990).
When we ask: What class of algorithms is it that
1) satisfy any boundary conditions;
2) is size invariant (without adjusting parameters);
3) is covariant;
we come away with one answer:
Laplace ![]() .
.
But of cause Laplace equation is too simple - it does not allude to
DNA, and it does not couple morphogen(s) to shape. How can one add significant
shape dependence so as to remain covariant and size invariant? One way
we can think of according to Cummings:
![]() .
.
If we assume

we get something very over akin to Brusselator or Turing system with
exception of coupling to form. These equations are appropriate, in principle,
for modeling of coupling dynamics of gene network expression and embryo
form changes. So we going to work out such modification of our model based
on the later equations.
In conclusion we should be mention following. Different mechanisms with
very different size-regulating properties may be operating within a single
organism in two orthogonal axes. For instance, in the antero-posterior
dimension of insects, there is no positive size regulation, there is even
a negative size regulation. But in the dorso-ventral dimension there is
well-known size regulation.
Reference List