M Tutorial (part 5/6)
In M, the following operations are allowed:
| <oper> | Meaning |
| 0 | 0 |
| 1 | <bool1> AND <bool2> |
| 2 | <bool1> AND NOT <bool2> |
| 3 | <bool1> |
| 4 | NOT <bool1> AND <bool2> |
| 5 | <bool2> |
| 6 | <bool1> XOR <bool2> |
| 7 | <bool1> OR <bool2> |
| 8 | NOT <bool1> AND NOT <bool2> |
| 9 | NOT (<bool1> XOR <bool2>) |
| 10 | NOT <bool2> |
| 11 | <bool1> OR NOT <bool2> |
| 12 | NOT <bool1> |
| 13 | NOT <bool1> OR <bool2> |
| 14 | NOT (<bool1> AND <bool2>) |
| 15 | 1 |
The entries with a darker background are the most important. This is because the AND, OR, NOT and XOR operands form the basis of all other computations. Any other combination can be derived from them. The programs below display the logic tables of these four operators.
INTFN117Þ;Program demonstrates intrinsic functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞW #,"The Boolean AND table"
ÞW !,"0 AND 0 gives ",$ZB(0,0,1)
ÞW !,"0 AND 1 gives ",$ZB(0,1,1)
ÞW !,"1 AND 0 gives ",$ZB(1,0,1)
ÞW !,"1 AND 1 gives ",$ZB(1,1,1)
ÞQ
INTFN118Þ;Program demonstrates intrinsic functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞW #,"The Boolean OR table"
ÞW !,"0 OR 0 gives ",$ZB(0,0,7)
ÞW !,"0 OR 1 gives ",$ZB(0,1,7)
ÞW !,"1 OR 0 gives ",$ZB(1,0,7)
ÞW !,"1 OR 1 gives ",$ZB(1,1,7)
ÞQ
INTFN119Þ;Program demonstrates intrinsic functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞW #,"The Boolean X0R table"
ÞW !,"0 X0R 0 gives ",$ZB(0,0,6)
ÞW !,"0 X0R 1 gives ",$ZB(0,1,6)
ÞW !,"1 X0R 0 gives ",$ZB(1,0,6)
ÞW !,"1 X0R 1 gives ",$ZB(1,1,6)
ÞQ
INTFN120Þ;Program demonstrates intrinsic functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞW #,"The Bollean NOT table"
ÞW !,"(B) NOT 0,0 gives ",$ZB(0,0,10)," adjusted ",$ZB(0,0,10)+2
ÞW !,"(B) NOT 0,1 gives ",$ZB(0,1,10)," adjusted ",$ZB(0,1,10)+2
ÞW !,"(B) NOT 1,0 gives ",$ZB(1,0,10)," adjusted ",$ZB(1,0,10)+2
ÞW !,"(B) NOT 1,1 gives ",$ZB(1,1,10)," adjusted ",$ZB(1,1,10)+2
ÞW !,"(A) NOT 0,0 gives ",$ZB(0,0,12)," adjusted ",$ZB(0,0,12)+2
ÞW !,"(A) NOT 0,1 gives ",$ZB(0,1,12)," adjusted ",$ZB(0,1,12)+2
ÞW !,"(A) NOT 1,0 gives ",$ZB(1,0,12)," adjusted ",$ZB(1,0,12)+2
ÞW !,"(A) NOT 1,1 gives ",$ZB(1,1,12)," adjusted ",$ZB(1,1,12)+2
ÞQ
The NOT table gives incorrect results in that numbers such as –2 can result from the $ZBOOLEAN function. –2 is not a binary number. We adjusted the results to correctly produce within the Boolean range 0 and 1by adding 2 to the function result.
Write a program
what will perform Boolean calculations based upon the AND, OR, XOR and NOT operators.
INTFN121Þ;Program demonstrates intrinsic
functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞN PHRASE,PSSWRD
ÞR #,"Enter a Phrase: ",PHRASE
ÞQ:PHRASE=""
ÞR !!,"Enter Password: ",PSSWRD
Þ; Use XOR to Encrypt
ÞS PHRASE=$ZB(PHRASE,PSSWRD,6)
ÞW !!,"Encrypted version: ",PHRASE
Þ; Use XOR to Decrypt
ÞS PHRASE=$ZB(PHRASE,PSSWRD,6)
ÞW !!,"Encrypted version: ",PHRASE
ÞQ
The above program is quite interesting as it demonstrates the property of XOR to reverse its effect. We prompt for a phrase and a password and XOR the two. The Encrypted version of the string is displayed. Then the encrypted version is then XORed with the same password and the original string is output. One thing worth noting is that $ZBOOLEAN can take practically anything and is not limited to Boolean variables only. In INTFN121 we are XORing strings. When doing such operations, the strings are converted to binary and are operated upon that way. If <bool1> is longer than <bool2>, <bool2> will be repeated over and over again.
Take a look at the diagram below to appreciate how XOR works.
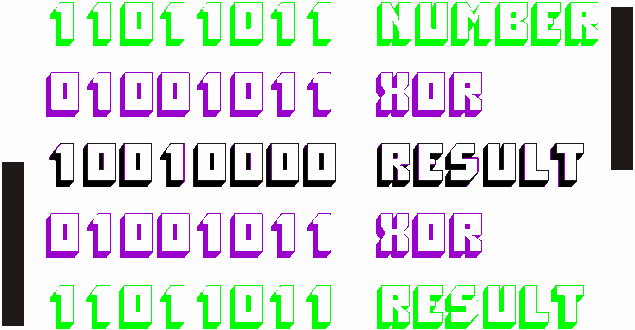
$ZCRC(<string>,<type>) or $ZCR(<string>,<type>)
INTFN122Þ;Program demonstrates intrinsic functions - Chris Bonnici - Sept 1997
Þ;M Web Magazine @ http://geocities.datacellar.net/SiliconValley/7041/mwm.html
Þ;You are using this program at your own risk
Þ;
ÞN PHRASE,CRC
ÞR #,"Enter a Phrase: ",PHRASE
ÞQ:PHRASE=""
ÞS CRC=$ZCR(PHRASE,1)
ÞW !,CRC
ÞR !!,"Renter Phrase: ",PHRASE
ÞI CRC'=$ZCR(PHRASE,1) W !!,"They don't match"
ÞE W !!,"Match OK!"
ÞQ
INTFN122 is used to compute a checksum of a string. Two checksums are provided, ASCII summation (setting <type> to 1) and XOR value of string. The latter is performed when <type> is set to 0.
ASCII summation basically adds together. The number displayed after you type in the string is this addition.
Write a
function using some of the intrinsic functions we’ve discussed to perform ASCII
summation.
Run INTFN122. When asked to enter the phrase type in ‘HELLO’. When asked to renter it type ‘EHOLL’. Do you have a match? How does this function work?
Modify the above program so that it works with the XOR value of the string. Try entering two phrases with the letters in mixed up order. How does this perform.
Some of you might doubt the validity of such a function. Granted that the function cannot be used to detect absolutely all changes, but it may prove useful in those situations were some detection is better than no detection. Just remember that an all OK does not necessarily mean all OK.
$ZHEX(<number>) or $ZH(<number>)
In this issue we talked about binary numbers. Now we peek at another numbering system, the hexadecimal system. In this numbering system we have 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F.
This function converts both ways. If the number is in quotes it is taken to be to base 16 (i.e. hexadecimal) otherwise it is considered decimal.
Before we head for our last topic, there is something you should know about functions and commands that commence with the letter Z; they may be implementation specific and you have not guarantee that they are available in other M implementations.
