(Abstracto del Documento Property-based Software Engineering Measurement)
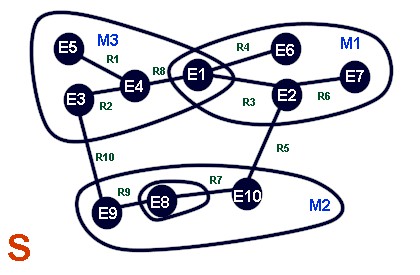
Representación de un sistema y de sus módulos
Definición general de complejidad
Definición formal de complejidad
Función Complejidad(S) aplicada a un sistema de telecomunicaciones públicas
Referencias mencionadas en esta página
En este trabajo se expone una propuesta de métricas de software basadas en propiedades mateáticas. su intención es el proporcionar una medida cuantitativa a varios conceptos de software, entre ellos la Complejidad.
En este trabajo la siguiente es la representación de un sistema computacional:
Un sistema S es representado como un par <E,R>, donde E representa el conjunto de elementos de S, y donde R representa el conjunto de las relaciones que existen entre los elementos de S
Dado un sistema S =
Em pertenece a E y ademas:
Rm pertenece a R.
Por ejemplo: E puede ser definido como un conjunto de estatutos de un código y R el conjunto de flujos de control entre estos estatutos de código.
La siguiente figura define gráficamente lo que nosotros entendemos como un sistema y sus módulos

Un Sistema S como el conjunto de sus elementos E y sus relaciones R. Organizado en subsistemas o Módulos M
La Complejidad es un concepto que es considerado extremadamente relevante para un sistema computacional, el cual ha sido abordado por varios investigadores. Es importante hacer notar que la definición de complejidad usada en este trabajo es intencionalmente mas restrictiva que la usada por otros investigadores [CSM79]. Esto nos permite proporcionar una definición de la complejidad de un artefacto a travéz de un conjunto definido de propiedades.
La Complejidad se define como una propiedad intrínseca de los artefáctos y no toma en cuenta la percepción de un observador externo. Nuestra intencion es claramente diferente de la expuesta en Curtis et al [CSM79] en donde se mide la complejidad de el software por el impacto que este tenga en otros elementos (como por ejemplo en la Gente).
En nuestras definiciones esperamos que la complejidad sea:
No Negativa (Propiedad Complejidad.1)
Y Nula (Propiedad Complejidad.2) cuando no haya relaciones entre los elementos de un sistema.
Puede ser punto de discución que la complejidad no es nula cuando no hay relaciones entre los elementos de un sistema por que cada elemento tiene una complejidad propia. Sin embargo, el enfoque dado en este trabajo mide la complejidad de un sistema que depende de las relaciones entre sus elementos y no como una propiedad de un elemento aislado.
La Complejidad que un elemento aislado puede agregar a un sistema bien puede ser el resultado de las relaciones entre sus sub-elementos. Por ejemplo, en un sistema modular, cada módulo puede ser visto como un "componente de alto nivel" el cual encapsula "subelementos". Si queremos considerar el sistema como compuesto solamente de estos "componentes de alto nivel", no debemos "desempacar" estos elementos para medir su complejidad y solo tomar en cuenta las relaciones entre los componentes de alto nivel.
Pero si deseamos tomar en cuenta la complejidad que aporta cada componente al sistema entonces el sistema debe de ser visto como la suma de los componentes y subcomponentes. Así como las relaciones totales del sistema son la suma de las relaciones entre componentes de alto nivel mas la suma de las relaciones de los subcomponentes.
La Complejidad no debe de ser sensitiva a las convenciones para representar la dirección de los arcos que representan las relaciones entre sus componentes. (Propiedad Complejidad.3) Un sistema y las relaciones entre sus componentes no cambian si cambiamos la forma de representarlos. por lo tanto la complejidad tampoco debe cambiar con este respecto.
De igual manera:
La complejidad de un sistema S debe ser igual o mayor que la suma de las complejidades de cualquiera de sus modulos m aun cuando no hay relaciones entre estos modulos pero estos comparten componentes. (Propiedad Complejidad.4)
Esto se explica porque al juntar módulos implícitamente genera más relaciones entre las entidades de estos módulos. (Relaciones de "definición" o "Uso" de los componentes unidos son creadas al juntar dos módulos de un sistema). Como consecuencia la propiedad Complejidad.4 tiene tamien otra forma de enunciarse.
La complejidad de un sistema nunca disminuirá cuando las relaciones entre sus componentes aumenten. (Propiedad Complejidad.4)
Se ha argumentado que no siempre es cierto que entre mas relaciones mayor la copmplejidad de el sistema. En algunos casos, el agregar relaciones entre componentes puede ayudar a entender mas al sistema. esto es desde luego cierto, pero lo que se mejora es el entendimiento de el sistema (esto es, la percepción de el sistema hecha por un agente externo, como la gente), y no la complejidad. La complejidad es solo un factor a aplicar para determinar el entendimiento de el sistema y puede ayudar a pronosticarlo, pero no es el único elemento que se deba de usar para medir el entendimiento de el sistema.
Por último:
La Complejidad de un sistema que se conforma de módulos disjuntos (que no comparten ni relacion ni componentes uno con otro) será igual a la suma de las complejidades de dichos módulos (propiedad Complejidad.5). Consistente con la propiedad Complejidad.4 si un sistema es conformado por dos módulos pero estos no son unidos (esto es que aun sean disjuntos) entonces, ninguna nueva relación es generada entre los modulos disjuntos.
Estas propiedades que se definen para la medición de la complejidad son, hasta cierto punto, una generalización de las propiedades que varios autores han ya proveido en la literatura. (Ref [LJS91, TZ92, W88] para la complejidad en el software, usualmente usadas para graficas de flujo de control. Nosotros las hemos generalizado porque de esta manera podremos usarlas en artefactos diferentes al código de software o a otras abstracciones diferentes a los flujos de control.
La Complejidad de un sistema S está dada por la función COMPLEJIDAD(S) la cual está caracterizada por las siguientes propiedades.
Propiedad Complejidad.1: No Negatividad
La Complejidad de un sistema S =
![]()
Propiedad Complejidad.2: Valor Nulo
La Complejidad de un sistema S =
![]()
Propiedad Complejidad.3: Symetría
La Complejidad de un sistema S =
![]()
Propiedad Complejidad.4 Monotonicidad de los módulos
La Complejidad de un sistema S =
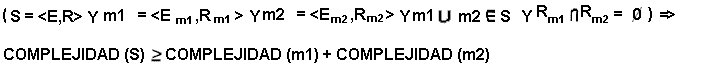
Por ejemplo: la complejidad de el sistema S mostrado en la figura siguiente es mayor que la complejidad de los modulos m1 y m2
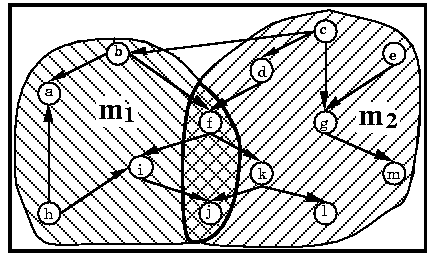
Ilustración de la propiedad complejidad.4
Propiedad Complejidad.5: Aditividad de modulos disjuntos
La Complejidad de un sistema S =
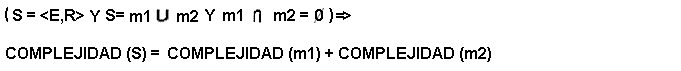
El MSC de el sistema de telecomunicaciones móvil descrito en este trabajo consta en promedio de 900 Módulos. estos Módulos tienen en promedio 100 relaciones con otros módulos. Así que el cálculo superficial de la complejidad de el MSC es:
COMPLEJIDAD (S) = (900,(100*900)) = 90000
El resultado de 90000 es un indicativo de que la complejidad en un nodo de telecomunicaciones móvil es bastante alta.
[CSM79]
B. Curtis, S. Sheppard, P. Milliman, M. Borst, T. Love,
"Measuring the
Psychological Complexity of Software Maintenance Task with the Halstead and
McCabe Metrics," IEEE Trans. Software Eng., vol. 5, no. 2, pp. 96-104, March
1979.
[LJS91]
K. B. Lakshmanian, S. Jayaprakash, and P. K. Sinha, "Properties
of Control-Flow
Complexity Measures," IEEE Trans. Software Eng., vol. 17, no. 12, pp. 1289-1295,
Dec. 1991.
[TZ92]
J. Tian and M. V. Zelkowitz, "A Formal Program Complexity Model
and Its
Application," J. Syst. Software, vol. 17, pp. 253-266, 1992.
[W88]
E. J. Weyuker, "Evaluating Software Complexity Measures,"
IEEE Trans. Software
Eng., vol. 14, no. 9, pp. 1357-1365, Sept. 1988.
![]()