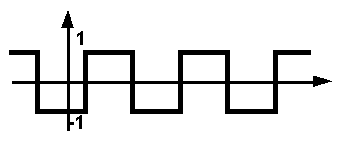Forord
Dette er en hovedoppgave ved Høyskolen i Oslo avdeling for ingeniør utdanning, våren 2000.
Denne oppgaven tar for seg virkemåte og problemstillinger ved design av en audio synthesizer og har som mål å belyse disse områdene og, hvis mulig, avslutte med komplett og funksjonell synth i hardware.
Elektronisk musikk har lenge vært et interesseområde for oss begge og når vi skulle velge avsluttende hovedprosjekt falt det naturlig å jobbe med elektronisk lydbehandling.
Vi vil i denne oppgaven først ta for oss de teoretiske aspektene ved en digital synthesizer og tilslutt praktisk implementasjon og test av ferdig kode og hardware.
Innholdet i denne oppgaven ligger litt på kanten av fagpensumet til de linjene vi tilhører her på skolen, som er Telematikk og Kybernetikk.
Arbeidet har derfor stort sett foregått selvstendig uten direkte faglig veiledning.
Vi vil allikevel gjerne si takk til Henry Johansen for hjelp med design og utlegg av kretskort og komponenter, Eirik Jensen ved Bit elektronikk for uvurderlig hjelp og informasjon i sammenheng med Analog Devices produkter, Stian Svendsen for utarbeiding av kabinett og Simen Filseth for hjelp med bilder til rapporten.
Til slutt vil gjerne takke vår prosjektveileder, Audun Weierholdt, for eksepsjonell goodwill og bistand ikke bare under prosjektarbeidet men også i løpet av de tre årene vi har gått på HiO IU.
Nils Petter Lyngstad Bror Gundersen
Denne oppgaven setter seg som mål å belyse forskjellige lydsyntese teknikker og DSP system design, for tilslutt å implementere en digital synthesizer.
Det diskuteres forskjellige synteses teknikker med spesielt fokus på subtraktiv syntese og hvordan denne teknikken kan realiseres i et DSP system. Dette vinkles spesielt mot Analog Devices ADSP21065L signalprosessor og Analog Devices EZ-LAB utviklingsplattform.
De forskjelllige blokkene ved subtraktiv syntese diskuteres og implementers i C kode. I tillegg diskuteres Audio effekter i sammenheng med lyd syntese
og implementeres i C.
Videre undersøkes forskjellige mikrokontroller teknologier og prinsipper spesielt rettet mot Amel M40400 mikrokontroller og Atmel EB01 utviklingsplattform. Problemstillingen rundt data innhentning med tanke på A/D omformere og mikrokontroller belyses og implementeres i maskin og programvare. Det utvikles også et egprodusert kretskort med oppgave å kople mikroprosessore systemene og A/D omformerne sammen.
Avslutningsvis integreres disse elemtene, med tilhørende programkode og kretskort utlegg, til en komplett digital syntheseizer.
Modulasjons og syntese teknikker.
Digitale filtre – Bilineære transformasjoner
Memory mapping av perifere enheter
Synthesiser programvare implementering
Analog Devices ADSP21065L SHARC DSP
Mikrokontroller - hardware prinsipper
ARM prosessor – I/O arkitektur
Atmel prosessor - Perifer arkitektur
Multiprosessorarkitektur – Kommunikasjon med prosessor på forskjellig
plattform
Komponenter i parallellbussystemet
Design av kretskort for sammenkobling av kit og plassering av
periferenheter
Mikrokontroller – software prinsipper
Innlesing av analog til digital konverter data
Parameter overføring – DMA til og fra SHARC DSP
Mikrokontroller – Software og hardware implementasjon
Atmel EB01 M40400 utviklingskit
Utviklings –software og -hardware
Hva kan så gjøres for å utbedre disse svakhetene?
Dokumentasjon for Sharc 21065L DSP prosessor, EZ kit utviklingskit og
ADI 1819 Codec
Dokumentasjon for Atmel mikrokontroller og mikrokontroller kit
Mikrokontroller periferkomponenter
Manualer til andre virtuelle analoge synther
Historie
Mennesket har alltid vært opptatt av musikk og utviklingen av forskjellige musikkinstrument har hele tiden fulgt den teknologiske utviklingen i samfunnet ellers.
Før 1900 tallet fantes det stort sett kun akustiske instrumenter . Et av de første elektriske instrumentene kom rundt århundreskiftet og ble laget av amerikaneren Thaddeus Cahill. Han laget en innretning han kalte Dynamophon. Denne bestod av en rekke dynamoer som ble styrt mekanisk og genererte forskjellige vekselspenninger innenfor det hørbare frekvensområdet. Disse spenningene ble igjen sendt via et elektrisk klaviatur, altså brytere, inn på telefonlinjer og til telefoner som igjen forsterket opp signalet ved hjelp av akustiske horn. En lite ulempe med denne maskinen var at den veiet nesten 200tonn , var omtrent 20 meter lang og laget alvorlig forstyrrelser på telefonnettet.
I 1939 kom The Hammond Organ CO’s novachord. Dette instrumentet baserte seg på 169 elektroniske vakuum rør som byggeblokker i 12 oscillatorkretser. Disse oscillatorene ble styrt av et elektronisk klaviatur. Dette instrumentet regnes som forgjengeren til dagens elektroniske audio synthesizere.
Det var først 1964 da Robert Moog konstruerte en transistor basert elektronisk synthesizer at elektroniske instrumenter foruten gitaren ble allment akseptert som noe det faktisk gikk an å lage musikk med.
Disse aller første analoge synthesizerene baserte lyd genereringen på subtraktiv syntese, som innebærer elektroniske oscillatorer og filtre. Etter dette skjedde utviklingen i takt med elektronikk revolusjonen. Synthene ble mindre, kraftigere, og fikk flere og flere stemmer.
Ved slutten av ’60-tallet og begynnelsen ’70-tallet kom de første forsøkene på å generere lyd ved hjelp av digitale computere. Datamaskinene var store og kostbare på denne tiden og var forbeholdt universiteter og store selskaper.
Etter hvert som den moderne mikroprosessoren ble tilgjenglig for konsum markedet, og på grunn av de analoge komponentenes problemer med stabilitet og temperaturdrift gikk de fleste synth produsentene over til digitale løsninger basert på sample avspilling teknikker.
Slike instrumenter programmeres ofte ved hjelp av trykk knapper og LCD display. Dette har ført til en lite intuitiv måte å jobbe med lyd på.
Med dagens raske og relativt billige Digitale Signal Prosessorer, DSP, og hjemme datamaskiner, har det dukket opp en rekke nye typer synthesizere. Mange er meget avanserte softwareprogrammer som kjøres på hjemmedatamaskiner og styres ved hjelp av musepekeren og tastaturet. En annen trend tar seg for mål å fortsatt lage fysiske synther basert på raske DSP prosessorer.
Det har blitt et behov blant musikere for enkle og intuitive musikkinstrumenter som er enkle å bruke. Derfor er det mange moderne synther som forsøker å emulere de gamle analoge synthene ved hjelp av raske signalprosessorer.
Denne typen syntheseizere kalles for Virtual Analog og kjennetegnes ved at de har mange fysiske kontroll velgere og er enkle i bruk uten behov for innviklet programmering.
Det moderne musikk studioet
Et studio oppsett inneholder stort sett en eller flere lydkilder, note sequencer, effekt enheter, en audio mikser og et opptaksmedium. I tillegg til dette kommer også en audio forsterker og høytalere.
I hvilken form disse enhetene opptrer kommer litt an på teknologien de benytter. Før i tiden var alt analogt, og de fleste delene hadde dedikerte hardware bokser. I dag blir mer og mer integrert i noen få hardware enheter. Et godt eksempel på dette er note sequencerern . En note sequencer er en enhet som sender ut note informasjon til lydkildene. Her programmeres note informasjonen enten direkte på seqenceren, eller via kontrollsignaler. I dag er den så godt som alltid implementert i et software program som kjøres på en datamaskin (PC/Mac). I tillegg blir det mer og mer vanlig å gjøre opptak direkte til hardisk på datamaskiner i samme program som sequenceren. Slike programmer, ofte kalt audio sequenserene, f. eks Stinberg’s Cubase eller Emagics’s Logic Audio, implementerer også en audio mikser slik at en fysisk miksepult i noen tilfeller er overflødig.
Som lydkilder brukes samplere og synthesizere. Dette kan være hardware løsninger, software løsninger eller en kombinasjon av begge.
For at et studio oppsett skal fungere tilfredstillende må enhetene kommunisere og utveksle kontroll signaler med hverandre.
De aller første analoge studioutstyret hadde ikke mulighet for å motta kontrollsignaler fra eksterne enheter. Det ble derfor utviklet et system, som ble kalt Control Voltage, eller CV, signalering. Med en slik løsning sendes det et analogt kontrollsignal mellom enhetene. Dette er et gammelt prinsipp og brukes ikke lengre i dag. Status quo er Musical Instruments Digital Interface, bedre kjent som MIDI. Dette er en digital kommunikasjonsprotokoll hvor de vanlige signalene, både note informasjon og generelle kontroll signaler, er definert og allment akseptert som en standard av utstyrs produsentene.
Trendene blant utstyrs produsentene går mot heltdigitale studio oppsett. I et digitalt studio blir audio signalene overført og prosessert på digital form hele veien fra lydkilde via mikser, til digital lagring på harddisk.
I et analogt studio har alle enheter analoge ut og/eller innganger. Moderne studioer er ofte hybride og benytter seg av både analogt og digitalt utstyr. Digitalt ustyr har derfor en digital-til-analog omformer på utgangene slik at de kan brukes sammen med annet utstyr på lik linje med analogt utstyr.
Prinsipper for lyd syntese
Det finnes forskjellige metoder for å generere lyd som oppfattes som musikalsk.
Som kjent består lyd av sinus bølger med forskjellige frekvenser, avhengig av tone og klangfarge. Målet for lyd syntese blir derfor å gjenskape tilsvarende frekvens spekter ved hjelp av forskjellige teknikker.
Subtraktiv syntese
Baserer seg på å generere et signal med et rikt harmonisk spektralinnhold. Dette signalet føres så inn på ett eller flere filtre. Disse er ofte av typen lavpass, høypass, eller
båndpass/båndsperre. Filtrene fjerner så en del av de harmoniske komponentene i frekvens spekteret slik at en mer presis tone og klangfarge blir igjen. Det er også vanlig å styre disse aktive elementene fra kontroll kilder.
Dette er den eldste og mest brukte av syntese teknikkene, hovedsklig fordi den er den enkel å implementere teknisk, i tillegg til at den er relativt enkel å bruke for musikeren.
Blokkskjematisk kan en subtraktiv syntese implementering se slik ut:
Figur 1, Subtraktiv syntese
Oscillator
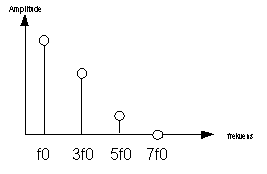
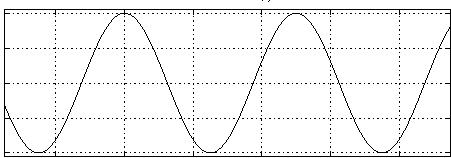
Oscillatoren er signalkilden i en subtraktiv syntese metode. Det er viktig at denne ikke er en ren sinus, siden sinus bølger ikke har harmoniske overtoner. Vanlige oscillator kurveformer er firkantbølge og sagtann bølge.
|
|
|
Figur 2, Firkant bølge og frekvensspekter
Filter
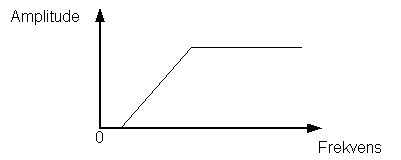
Et filter har som oppgave å slippe igjennom noen frekvenser og å hindre andre. Et lavpassfilter slipper derfor igjennom lave frekvenser og sperrer for høye frekvenser. Grensefrekvensen kalles knekkfrekvensen.
Under følger en figur som viser hvordan et
lavpassfilter behandler forskjellige frekvenser.
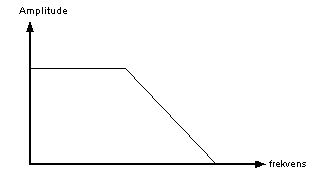
Figur 3 Frekvensrespons for et lavpassfilter
Figur 4, Høypass frekvensrespons
Av fysiske grunner lar det seg ikke gjøre å lage et filter som kutter helt ved knekkfrekvensen. Steilheten på dempningsflanken til filteret avgjør hvilken orden filteret har. Brattere kurve tilsvarer høyere orden. Høyere ordens filtre har også ofte en topp akkurat i knekkfrekvensen. Denne toppen kommer av en resonans i filtersystemer og gir en forsterkning for de frekvensene som ligger i knekkområdet. Det er derfor vanlig å kunne justere denne høyden på denne toppen.
Figur 5, 2.4.6.orden frekvensresponser
Det er viktig at filteret kan sveipes opp og ned i frekvens for å kunne regulere frekvens innholdet. Filteret må derfor kunne ta imot informasjon fra en kontrollkilde, for eksempel en LFO eller en omhylningskurve generator.
LFO
For å skape variasjon i lydbildet brukes forskjellige kontrollkilder til å styre de enkelte blokkene i systemet. En lavfrekvent oscillator er mye brukt til dette formålet.
Den enkleste formen for LFO er en sinusgenerator hvor frekvensen kan velges av brukeren.
Omhylningskurver
Det er ofte at det er ønskelig med andre kontrollsignaler enn repetitive signaler som oscillatorer. Omhylningskurver er en tidsbegrenset kurveform hvor formen kan justeres og til en viss grad velges av brukeren. En slik omhylningskurve betegnes ofte som en ADSR kurve etter navnet som er gitt på de forskjellige segmentene kurven består av. A står for Attack, D står for Decay, S står for Sustain og R for Release.
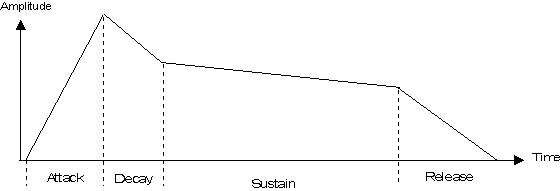
Figur 6, ADSR omhylningskurve
AMP
For å få riktig styrke på signalet siter det alltid en liten forsterker i enden av signalveien. Det er standard praksis at denne blokken inneholder en ADSR omhylningskurve.
Denne blokken tar også imot kontrollsignaler fra LFO og omhylningskurver.
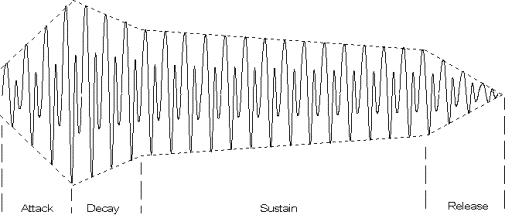
Figur 7, Sinusbølge med omhylningskurve
Modulasjons og syntese teknikker.
Disse teknikkene baseres på prinsippet med at to relativt enkle bølgeformer kan modulere hverandre for å skape en mer komplisert bølgeform. De mest kjente metodene baserer seg på kjente teknikker fra teleteknikk, amplitude og frekvens modulasjon. Det er vanlig å finne disse funksjonene i tillegg til de vanlige kurveform oscillatorer i analoge synther.
Amplitudemodulasjon betyr at den ene bølgeformen styrer amplituden på den andre.
Frekvensmodulasjon vil si at den en ene bølgeformen styrer frekvensen til den andre.
PCM Wavetable
Små opptak, eller samples, lagres i minnet og spilles av. Lyd samplet går ofte gjennom en lydbehandlings algoritme før det sendes til utgangen, dette er derfor en hel digital teknikk.
Dette er en meget populær syntese teknikk siden den er enkel å implementere og krever i utgangspunktet svært liten prosessor kraft. De aller første digital synthene benyttet denne typen syntese. Her brukes da korte samples av bølgeformer som loopes, og derved virker som oscillator.
Hvis man også kan ta opp (sample) analoge signaler kalles det sampling.
Fysisk modellering
En relativt ny teknikk som benytter en matematisk modell av et akustisk instrument. Ta for eksempel en fløyte. Alle de fysiske karakteristikkene som utgjør en fløyte blir en variabel i en matematisk algoritme. Ved da å forandre variabelen for lengden av fløyten, vil lyden bli dypere. Siden denne teknikken krever avansert matematisk behandling stilles det også store krav til DSP systemet som programvaren kjører på. Denne teknikken er derfor ikke veldig utbredt.
Additiv syntese
Dette er som navnet tilsier det motsatte av subtraktiv syntese. Her genereres de harmoniske spektralkomponentene hver for seg og som til sammen generer en kompleks bølgeform med ønsket lyd og klangfarge.
Synther basert på denne teknikken bruker ofte en matematisk metode som kalles Inverse Fast Fourier- Transformasjoner, IFFT. Her er spektral komponentene kun matematiske operatorer i en formel som genererer en kompleks bølgeform.
For å få god nok kontroll på en lydredigerings algoritme basert på IFFT kreves det mye prosessorkraft. Ved å først analysere et analogsignal ved hjelp av vanlig FFT for å modifisere det i frekvensplanet, for tilslutt inverstransformere ved hjelp av IFFT tilbake til tidsplanet, kalles Resyntese
Dette er den hittil mest prosessorkrevende teknikken og uhyre få synther benytter seg av dette prinsippet. Det finnes sannsynligvis noen få avanserte software baserte løsninger som gjør det.
Signalbehandling
Analoge signaler er tids kontinuerlige, digitale signaler er tidsdiskrete
Figur 8, Eksempel på et tidskontinuerlig signal.
Figur 9, Eksempel på et tidsdiskret signal
Sampling
For å gjøre et tidskontinuerlig signal tids diskret, må det punktprøves. Det å punktprøve noe vil si å måle en momentanverdi av et tidskontinuerlig signal. En slik momentanverdi representeres ved en tallverdi. En enhet som utfører dette kalles en Analog-til-Digital omformer.
Figur 10, Prinsipp skisse for punktprøving
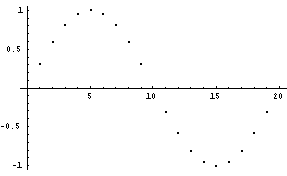
Figur 11, Et punktprøvet sinussignal.
Nyquist
For at et punktprøvet signal skal kunne gjenskapes som et tidskontinuerlig signal er det en nedre grense for frekvensen til punktprøvingssignalet i forhold til det signalet som skal punktprøves.
Dette forholdet kalles Nyquist’s punktprøvingsteorem, og slår fast at punktprøvingsfrekvensen minst må være dobbelt så høy som det signalet som skal punktprøves. Hvis dette forholdet ikke respekteres oppstår det som kalles aliasing.
Aliasing vil si at frekvenskomponenter fra det spektrumet som oppstår når noe punktprøves, finner veien inn i det punktprøvede signalet. Dette oppfattes av en lytter som en pipetone som ikke hører hjemme i lydbildet.
For å garantere at aliasing ikke skal forekomme båndgrenses det signalet som skal punktprøves med et lavpassfilter før det kommer til A/D omformeren. Knekkfrekvensen på et slikt filter er lik halvparten av den punktprøvingsfrekvensen som brukes. Et slik filter kalles derfor for et Anti-aliasing filter.
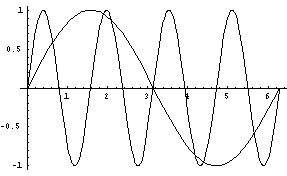
Figur 12, Aliasing
Siden punktprøvingsfrekvensen er konstant for de fleste digitale systemer, er det derfor gitt en øvre grense for hvor høye signaler et musikk systemet skal kunne behandle. Vanlige tall på punktprøvingsfrekvensen er 44.1kHz eller 48kHz. Den høyeste frekvenskomponenten et signal da kan inneholde blir i praksis rundt 20kHz.
Digital til analog omforming
Når et punktprøvet signal skal gjenskapes sendes det til en Digital-til-Analog omformer.
Det finnes flere prinsipper for å rekonstruere det analoge signalet. En vanlig måte er å benytte en såkalt trappetrinn omformer. Her holder D/A omformeren nivået på det punktprøvede signalet konstant, helt fram til neste punktprøvet. Denne sekvensen repeteres så for neste punktprøve. Et annet navn på dette prinsippet er ”Sample&Hold”.
Signalet som kommer ut av en slik D/A omformer er ofte hakkete, derav navnet. For å eliminere disse nivåsprangene plasseres det et lavpass filter som siste ledd i D/A prosessen. Dette filteret kalles for et Post-Image filter.
Z-transformasjoner
For at det skal være mulig å implementere matematiske funksjoner i digitale systemer trengs det et matematisk verktøy. Z-transformasjoner gir en metode for å speile et tidskontinuerlig signal, et differensialt system, over til et tids diskret differens system.
Ved å benytte slike transformasjoner får man en måte å benytte rasjonale funksjoner på tids diskrete signaler.
Et lengde begrenset punktprøvet signal
x[n] med lengde N kan beskrives som :
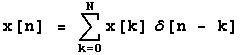
Hvor x[n] representerer en enkelt punktprøve i datastrømmen og d er en enhetsimpuls.
Z transformasjonen til et slikt signal
x[n] er da definert som :
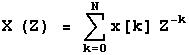
Hvor z representerer et hvilket som helst komplekst tall og er den uavhengige (komplekse) variabelen til z-transformasjonen. Størrelsen på eksponenten til z forteller om tidsplasseringen til x. For kausale systemer er denne eksponenten negativ, som tilsvarer en forsinkelse. Z^-1 betyr derfor ”forrige punktprøve”
For analoge systemer er vi kjent med at komplekse vinkelfrekvenser kan substitueres med Laplace transformasjon variabelen s, på formen s=jw.
På samme måte har vi en sammenheng mellom z og w på formen z=e^jw, hvor w er digital vinkelfrekvens 2 pi f/fs.
Z-transformasjoner brukes derfor på samme måte i tidsdiskrete systemer som Laplace transformasjoner i tidskontinuerlige systemer.
Filter design
Et filter er en essensiell blokk i et lyd syntese system. Som tidligere nevnt er et filter et system som slipper noen frekvenskomponenter igjennom udempet og andre ikke. For å få en forståelse av digitale filtre kan det vært greit å først se litt på analoge implementasjoner.
Analoge filtre
For å differensiere forskjellige frekvenskomponenter er vi avhengige av elektriske komponenter som er frekvensavhengige. Spoler og kondensatorer er gode eksempler på dette. En kondensator er en komponent som lagrer elektrisk ladning og en spole lagrer et elektromagnetisk felt. Disse er komplementære når det gjelder frekvensrespons ved at ’motstanden’ i en kondensator minker ved økende frekvens og for en spole øker den. Disse egenskapene kan representeres matematisk ved XL = j 2 pi f L og XC = 1 /(j 2 pi f C) som beskriver komponentenes komplekse motstand (impedans) XL og XC. L er spolens induktans i Henry, C er kondensatorens kapasitans i Farad og f er frekvens.
Et enkelt lavpass filter kan derfor lages ved å benytte seg av disse komponentene.
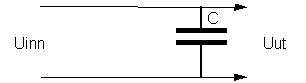
Figur 13, Enkelt analogt lavpassfilter
For å få en skarpere dempning settes flere slike filtre etter hverandre i signal veien. Ved å brukes to filtre har man et 2.ordens system osv. Ved høyere ordens systemer kan det oppstå en skarp forsterkning akkurat ved knekkfrekvensen. Denne toppen oppstår på grunn av en resonans som oppstår mellom komponentene i filtret. Denne resonansen er ikke ønskelig i konvensjonelle filter anvendelser. Ved lydsyntese og spesielt ved subtraktiv syntese er denne resonansen meget spennende og gir opphav til en rekke unike lyder.
Dette systemet kan beskrives matematisk ved:
som kalles filterets overføringsfunksjon
Digitale filtre – Billineære transformasjoner
Det finnes to typer digitale filtre, FIR (Finite Impulse Response) og IIR (Infinte Impulse Response). Forskjellen på disse er at FIR prinsippet baserer seg på å etterligne det signalet filtret gir ut etter det har blitt utsatt for en enhetsimpuls (Dirac puls). Dette prinsippet er relativt enkelt og lite prosessorkrevende. En egenskap ved disse filtrene er at de alltid er stabile og har derfor heller ikke resonans. Dette er uheldig for subtraktiv syntese og egner seg derfor ikke til dette formålet.
IIR metoden ligner mer på det analoge filter løsningen siden det her utledes filterkoeffisienter som signalet gjennomløper på en rekursiv måte, omtrent det samme som skjer inne i et analogt filter.
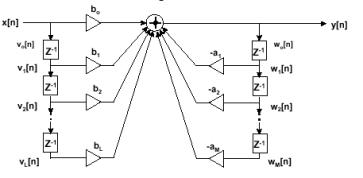
Figur 14, IIR blokk skjema
For å komme fram til et digitalt filter er det ofte enklest å gå veien om et analogt filter ved å benytte seg av sammenhengen mellom s og z. En velkjent metode går under betegnelsen Billineære transformasjoner. Denne metoden ender opp med et IIR filter, og benytter seg av sammenhengene : s = f(z) , s=jw og z=e^jw og er definert ved at s=f(z)= 1-Z^-1/1+Z^-1.
Ved å bruke overføringsfunksjonen vi fant for det analoge filteret kan vi nå ved hjelp av en bilienær transformasjon skape et uttrykk for et digitalt IIR filter.
For å bestemme konstantene må vi vite ønsket karakteristikk på filteret. Det finnes nå flere muligheter avhengig av hvilke egenskaper man ønsker å tilegne filteret. For de mest kjente filtertypene, Bessel, Chebyshev og Butterworth finnes det nå veldefinerte metoder for å bergene konstantene. En ulempe med disse filtertypene med tanke på synhtesizer design, er at ingen av disse filtertypene utvikler resonans ved knekkfrekvensen.
En mulig fremgangsmåte er beregne komponent verdiene i det analoge filteret slik at resonans oppstår.
Et annet viktig punkt ved designprosessen blir å lage filteret slik at både knekkfrekvens og resonans skal kunne varieres i sanntid. Et kritisk moment er nå å holde filteret stabilt. Et ustabilt filter vil raskt danne en meget kraftig resonans som vil, i hvert fall matematisk, øke til det uendelige.
Et stabilt filter defineres ved at røttene til både teller og nevner polynomet i filterets overføringsfunksjon, er mindre enn 1.
Ved å kun variere f. eks kondensator verdien i den analoge kretsen kan filteret fort bli ustabilt og dermed ubrukelig i musikk sammenheng.
En mulig løsning på dette er å anvende en teknikk som kalles Pol og nullpunkt design.
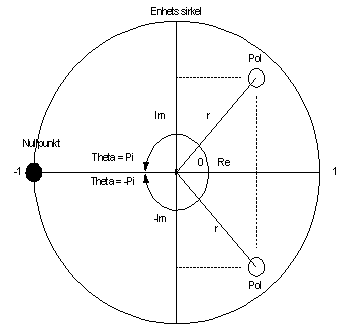
Pol/Nullpunkt design
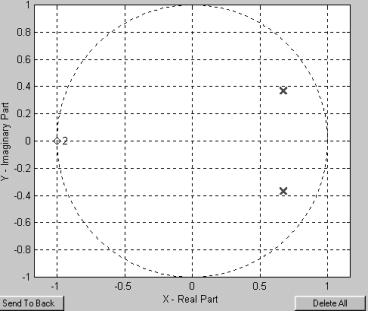
For å få en bedre oversikt over filterets stabilitet benyttes en Pol og nullpunktsanalyse.
Hvis tellerpolynomet i filterets overføringsfunksjon H(z) er lik null sies det at filteret har et nullpunkt for denne frekvensen. Tilsvarende har filteret en pol ved den frekvensen nevnerpolynomet er lik null. Dette kan forståes grafisk ved å plotte alle polene og nullpunktene inn i en enhetssirkel, hvor realdelen er langs x-aksen, og imaginærdelen er langs y-aksen. Så lenge alle polene og nullpunktene ligger innenfor denne sirkelen (avstanden fra et punkt og origo <=1 ) er filteret stabilt.
Figur 15, Eksempel på Pol og nullpunkt plassering i en enhetssirkel
Pol og nullpunkts design prosessen er motsatt i forhold til mange andre fremgangsmåter. Man starter her med pol og nullpunktsplasseringen i enhetssirkelen og regner seg bakover for å rekonstruere teller og nevner polynomet. På denne måten regner man seg fram til koeffisienter som garanterer et stabilt filter.
Den digitale vinkelfrekvensen strekker seg fra –pi til pi. Dette er tilsvarende kjent som Nyquist intervallet. I frekvensplanet tilsvarer dette –fs/2 til fs/2, hvor fs er punktprøvingsfrekvensen. Av denne grunnen får man en dempning av frekvenser tilsvarende fs/2 hvis nullpunktene legges ved +-pi. Tilsvarende hvis en pol legges ved 0. Da forsterkes lave frekvenser. Jo nærmere punktene legges enhetssirkelen, jo mindre blir bredden på forsterkningen eller dempningen, og utslaget blir mer ekstremt. Hvis punktet ligger på enhetssirkelen er båndbredden 1 (egenresonans) og forsterkningen kan fort bli >100db.
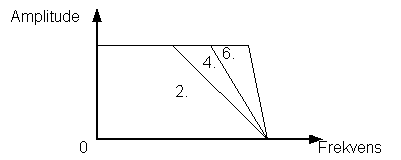
Ved å plassere poler og nullpunkter ved ønsket frekvens og resonans kan man realisere et filter. For å oppnå best mulig resultat bør filteret ha like mange nullpunkt og poler. Et andre ordens system har to poler, et fjerde orden har fire osv.
En ulempe med denne metoden er at man aldri kan plassere knekkfrekvensen absolutt, siden denne alltid er litt forskjøvet i forhold til resonansfrekvensen.
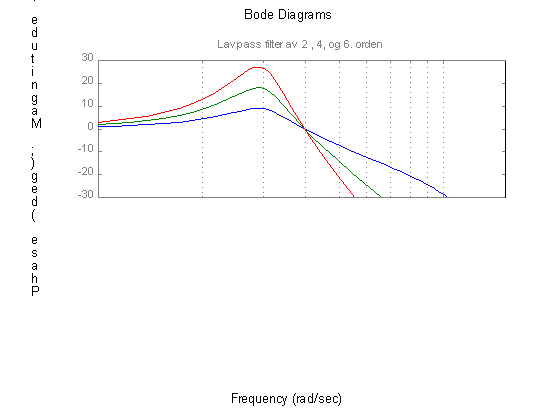
Figur 16, 2.,4. og 6. ordens filter med sammenfallende poler.
DSP system arkitektur
I de tilfellene der det er behov for matematisk behandling av signaler er det vanlig å benytte seg av en Digital Signal Prosessor, DSP. En DSP er en mikroprosessor som er spesiallaget for matematiske operasjoner. Hvis det er analoge signaler som skal behandles, må signalene punktprøves i en analog til digital omformer før de kan sendes til prosessoren. Når de er på digital form representeres de ved en tallverdi.
En DSP kan da lese inn tallverdiene og gjøre matematiske operasjoner på signalet.
Figur 17, Prinsipp skisse for et DSP system.
Mikroprosessor teknologi
Måten en konvensjonell mikroprosessor implementerer matematiske funksjoner er ved hjelp av enkle addisjoner og subtraksjoner og logiske operasjoner (OG, ELLER og IKKE). Dette skjer i en egen blokk i prosessor arkitekturen som kalles aritmetisk logisk enhet eller ALU (fra engelsk Arithmetic Logic Unit). Dette vil si at for å implementere en multiplikasjon må det skives et lite program som utfører en rekke addisjoner og subtraksjoner. I en signalprosessor hvor disse operasjonene brukes hele tiden, finnes det en egen blokk som tar seg av dette. Denne enheten kalles MAC (Multiply ACcumulator), og bruker ofte kun en klokkepuls på en multiplikasjon sammenlignet med minst 10 eller flere uten, avhengig av tallenes størrelse og prosessor type.
Det finnes to måter å representere et tall i en prosessor. Det formatet konvensjonelle mikroprosessorer oftest benytter er ”fixed-point” formatet. Her representeres tallverdien i to komplement binær form.
Siden de matematiske operasjonene som brukes i digital signal behandling krever desimal tall, egner heltalls aritmetikk seg dårlig til dette formålet. Derfor benytter digitale signalprosessorer seg av ”floating point” eller flyttalls formatet. Her representeres en tallverdi som et eksponentialtall. Ett bit brukes til fortegn og de resterende brukes til å beskrive mantissen og eksponenten. En DSP har derfor en egen FPU ( Floating Point Unit) blokk i intern-arkitekturen.
Figur 18, Floating Point enhet
Som det går fram av figurene ovenfor er størrelsen på de interne registrene som lagrer tallverdien vesentlig for hvor stort tall som kan representeres, eller presisjonen til et flyttall.
Hvis en DSP sies å være på 32bit betyr det at registrene er på 32 bit. Det finnes imidlertid noen typer prosessorer hvor den eksterne databuss bredden er mindre enn register størrelsen. Disse betegnes da som f. eks en 16/32 bits prosessor.
For at en DSP skal kunne utføre aritmetikk på et signal må den arbeide på en langt høyere hastighet enn den signalstrømmen den skal behandle. Dette vil i praksis si at den må være raskere enn punktprøvings frekvensen til den A/D eller D/A omformeren som benyttes. Årsaken til dette er at prosessoren må kunne utføre tilstrekkelig mange flyttallsoperasjoner i den tiden som er tilgjenglig mellom to punktprøver.
På grunn av forskjeller i den intern arkitekturen ved ulike signal prosessorer, kan ikke hastigheten til prosessoren leses direkte ut fra den klokkehastigheten den jobber på.
Det som i realiteten bestemmer hastigheten er hvor mange flytallsoperasjoner som prosessoren kan utføre i sekundet, eller MFLOPS, Million FLoating-point Operations Per Second.
Tilsvarende måles konvensjonelle mikroprosessorer i MIPS, Million Instructions Per Second
I noen arkitekturen utføres flere operasjoner på en klokkepuls.
Minne håndtering
Et viktig moment i hvordan en DSP fungerer er hvordan den organiserer minnet. De fleste konvensjonelle mikroprosessorer har store mengder eksternt minne. Inne i selve prosessoren finnes det kun et lite hurtiglager, cache, som lagrer de mest brukte instruksjonene.
En DSP derimot benytter ofte mer internt minne. Ved å plassere arbeidsminnet internt i prosessoren kan den jobbe mot dette minnet med høyere hastighet enn hva man kan på den eksterne databussen.
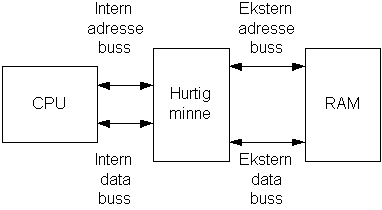
Figur 19, CPU system
Harvard arkitektur
Et område som en DSP skiller seg fra en mikroprosessor er at signalprosessoren ofte baserer seg på Harvard arkitektur. Harvard arkitektur vil si at istedenfor å ha ett stort eksternt minneområde med en data og en adressebuss, benyttes flere uavhengige data og instruksjons busser. Hensikten med denne arkitekturen er at disse bussene kan brukes parallelt slik at flere operasjoner kan utføres per klokkepuls.
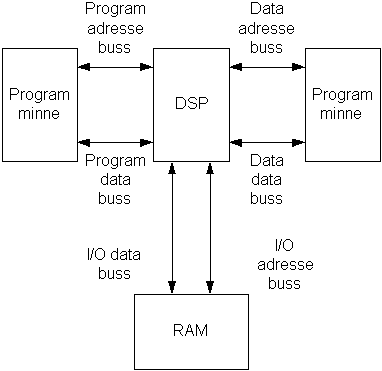
Figur 20, Harvard arkitektur
Sirkulær adressering
Når en DSP utfører en funksjon innebærer ofte dette at de samme dataene benytter rekursive operasjoner flere ganger i algoritmen. For å unngå å utføre en rekke adresseringer til det samme minneområdet bruker noen signalprosessorer en teknikk som kalles sirkulær adressering. Med en slik enhet defineres det minneområdet hvor dataene ligger av brukeren og resten styres av maskinvaren. En slik enhet forbedrer ytelsen på prosessoren i stor grad når det gjelder digital signal behandlings algoritmer.
DMA
Direct Memory Access, DMA er en egen prosessor som jobber sammen med selve kjernen i en DSP. Som navnet sier jobber denne prosessoren mot minne slik at ved store dataoverføringer kan DSP-kjernen overlate dataoverføringen til DMA prosessoren, slik at kjernen kan fortsette med program eksekveringen. Dette er meget viktig i multiprosessor systemer og andre systemer med hyppige dataoverføringer. Med tanke på digitale audio hvor det går en kontinuerlig dataflyt er det viktig at DMA kontrolleren kan kommunisere med A/D, D/A omformerne.
Memory mapping av perifere enheter
En annen problemstilling ved et signalprosesserings system er hvordan eksterne enheter kan koples sammen med en DSP. Den mest brukte måten er ”Memory Mapping”. Det vil si å lage adresserings systemet slik at hvis prosessoren adresserer minneplasser utenfor det fysiske minneområdet, velges den perifere enheten. På denne måten blir kommunikasjonen mellom prosessor og perifer enhet enkel og oversiktlig for programmereren.
Synthesizer programvare implementering
For å implementere en digital audio synthesizer er det viktig å finne ut hvilke blokker et slikt system består av. Vi hadde på forhånd kjennskap til den klassiske subtraktive syntesen:
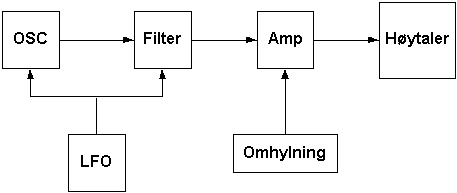
Figur 21, klassisk subtraktiv syntesesystem.
For å finne ut hvordan lyd syntesen blir gjort i praksis valgte vi å se nærmere i eksisterende synther i den såkalte Virtual Analog sjangeren. Vi gikk litt i sømmene på både det svenske firmaet Clavia’s NordLead 1 og det tyske firmaet Waldorf sin Q. De tekniske detaljene med antall stemmer, modulasjons matriser og lignende, var ikke spesielt viktig i denne prosessen siden vi regnet med at de ville bli vanskelig å overgå. Vi la mer vekt på hvilke enheter som er med i lyd algoritmen og hvilke fysiske kontrollere de gir brukeren tilgang til, for å forsøke å designe noe tilsvarende.
Lyd algoritmen
For å få en oversikt over hvilke elementer vi burde ha med i lyd algoritmen valgte vi å kikke på blokkskskjemaene til NordLead og Q.
Ser vi først på NordLead ser vi at denne passer bra med standard oppsettet. Blokker som skiller seg ut er Støy blokken.
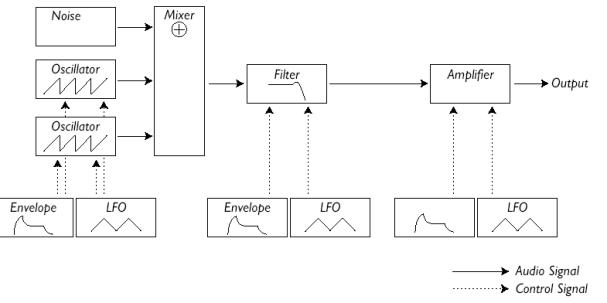
Figur 22, Clavia Nordlead 1.0 prinsippskisse
Q synthesizeren er en dyrere maskin enn NordLead og
har blant annet en del avanserte note sekvensierings funksjoner som faller litt
på utseiden av denne oppgaven.
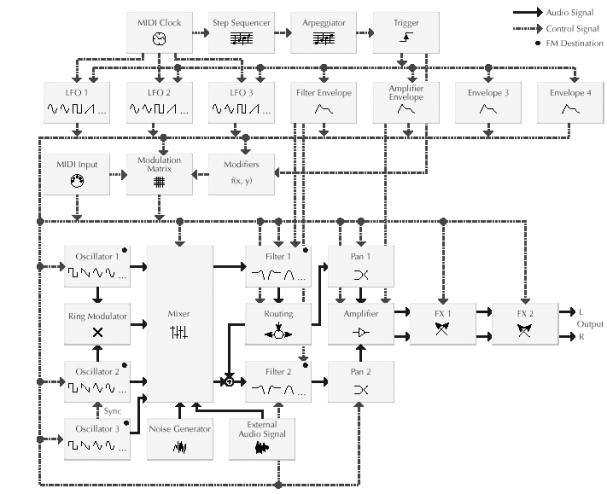
Figur 23, Waldorf Q prinsippskisse.
Som vi ser har Q en relativt avansert lyd algoritme. Blokker som vi syntes var verdt å merke seg var:
o MIDI kontroll
o Filter omhylningskurve
o Ringmodulasjon av oscillatorene
o Panorering
o Effekter
Siden noe av hensikten med denne oppgaven var at vi skulle belyse de forskjellige komponentene i en audio synth valgte vi å forsøke å implementere flest mulig forskjellige blokker, men å holde disse implementasjonene relativt enkle. I tillegg til de blokkene vi har lånt fra Q og NordLead ville vi se litt på FM og pulsbreddemodulasjon.
Algoritmen vi kom fram til ble denne:
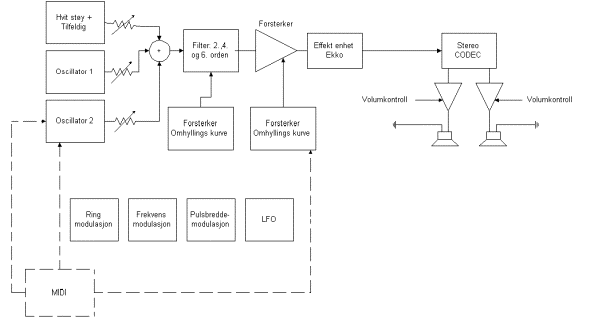
Figur 24, prinsippskisse for vår synthesizer
Hardware implementasjon
DSP
Da vi valgte denne oppgaven hadde vi ikke jobbet med digitale signalprosessorer før, og begynte med å hente inn informasjon om forskjellige typer og fabrikanter. Vi kom tidlig i kontakt med Bit elektronikk som er den norske importøren til Analog Devices. Vi ble invitert til et seminar som tok for seg deres DSP prosessor sortiment, og spesielt ADSP21065L prosessoren. Dette seminaret ga oss god innsikt i hvordan denne prosessoren fungerer med tanke på digital audio. I tillegg til informasjon, fikk vi også et komplett utviklingskort, EZ-LAB, på dette seminaret. Siden dette kortet inneholdt de fleste av de funksjonene vi regnet med å trenge til denne oppgaven valgte vi å satse på denne plattformen uten videre evaluering og undersøkelser av andre prosessor typer, for eksempel Motorola’s DSP563xx serie.
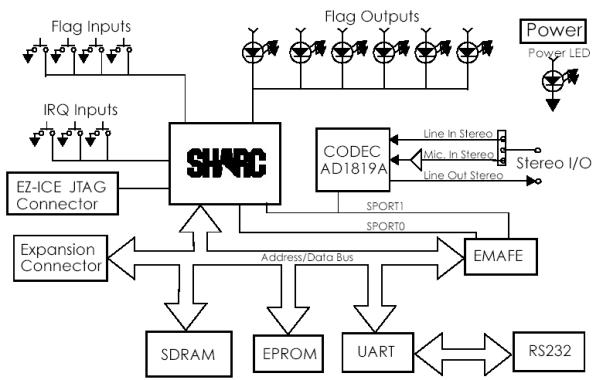
EZ_LAB
EZ-LAB plattformen fra Analog Devices benytter
Analog’s ADSP21065L SHARC signal prosessor. Integrert er også en stereo koder
og dekoder, eller codec på fagspråket. Denne tillater 16bit 48kHz stereo både
inn og ut av kortet. I tillegg til dette har det 2MB SDRAM som kan leses eller skrives på 1 klokkepuls.
Kortet har også 7 trykknapper og 6 lysdioder. Kortet koples opp mot en PC ved
hjelp av en RS-232 serieport.
Det er også mulig å kople eksterne enheter til kortet enten via en ekspansjonsbuss eller utvidelses kontakt (EMAFE).
Analog Devices
ADSP21065L SHARC DSP
Prosessoren som sitter på EZ-LAB kortet er, som nevnt tidligere, en ADSP21065L DSP, som benytter seg av Analogs SHARC arkitektur. Dette er en arkitektur basert på Harvard prinsippet, derav navnet Super Harvard ARCitecture.
Denne prosessoren har hele 4
uavhengige busser og tillater derfor en MAC operasjon, en subtraksjon
eller addisjon og lese eller skrive på
både Program og Data - databussene per klokkepuls. Denne prosessoren er et godt
eksempel på en moderne signalprosessor og brukes ofte i digitalt musikk utstyr. Her er
en kort teknisk oppsummering av prosessoren.
·
4 uavhengige busser
o
Program
memory address bus
o
Program
memory data bus
o
Data
memory address bus
o
Data
memory data bus
· 60MIPS
· Opp til 190 MFLOPS (130MFLOPS kontinuerlig)
·
32 bit
data
·
40bit
FPU
· 32 eller 40 bit sirkulær adressering
· 136k x 32bit internt minne
· Opp til 64M x 32bit eksternt minne
· 10 kanaler DMA
· 2 serieporter
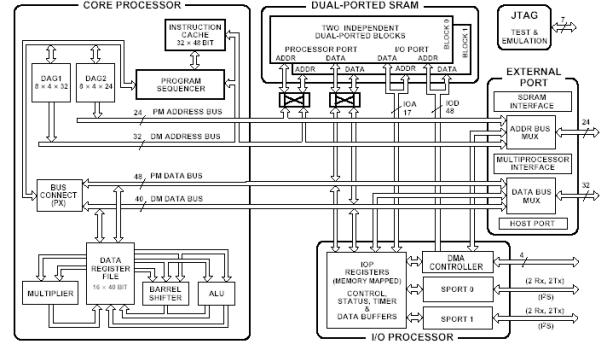
Figur 26, ADSP21065L intern arkitektur
Som det kommer fram av de tekniske spesifikasjonene passer denne prosessoren utmerket til vårt formål med tanke på prosessorkraft og mulighet for tilkopling av andre enheter via DMA og serieporter.
AD1819
Codec kretsen som sitter på EZ-LAB kortet er en universell IC som er beregnet på multimedia applikasjoner som lydkort til datamaskiner, telefon modem og DSP systemer. Den kan programmeres fra eksterne enheter og benytter 16bits A/D-D/A omforming med opp til 48kHz punktprøvingsfrekvens. Dette gir et signal/støy forhold på over 90db.
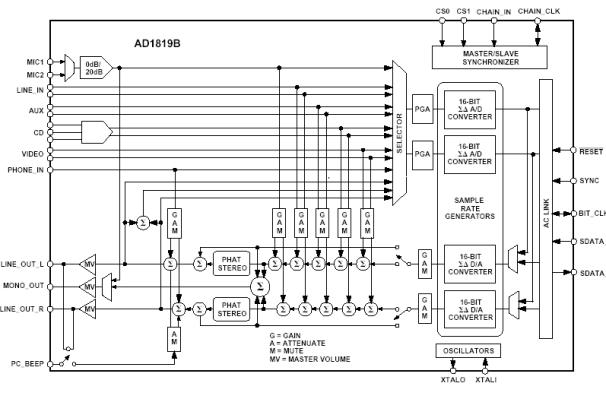
Figur 27, AD1819 blokkskjema
Mikrokontroller - hardware prinsipper
Valg av mikrokontroller
Etter å ha lagt linjene for selve synthesizerens hovedstruktur kom utfordringen til å tegne ned detaljene for systemets struktur. Sentralt for systemet, ved siden av lyd og effektenhetene, står mikroprosessoren. For å velge riktig mikroprosessor for systemet måtte en rekke parametere vurderes. Sammenligningsgrunnlaget vårt var:
- Intern og ekstern databussbredde forhold til DSP prosessorer og periferenheter.
- Intern og ekstern adressebussbredde i forhold til DSP prosessorer og periferenheter.
- Ytelse i forhold til klokkehastighet.
- Inn-ut ytelse på seriebusser og parallellbusser.
- Pris kontra ytelse
- Tilgjengelighet av utviklingsverktøy – både på hardware og software plattform.
- Effektforbruk i forhold til ytelse.
Valget falt på Atmels AT91M40400. Denne prosessoren kombinerer, sammenlignet med konkurrentene, flest av våre krav. De over nevnte punktene blir adressert i de videre avsnittene.
ARM – Atmel arkitektur
Atmels AT91M40400 er en mikrokontroller bygget rundt ARM’s ARM7TDMI Arm/Thumb prosessorkjerne. Atmel har bygget periferenheter rundt kjernen som er meget nyttige for vårt formål, bl.a. har prosessoren innebygde serieport kontroller, parallellbusskontrollere og avbruddkontrollere som er sentrale for synthens hardwarearkitektur, samt at det finnes minne, RAM, innebygget i kontrolleren.
ARM7TDMI kjernen er bygget opp etter RISC prinsippet, dvs. med et redusert instruksjonssett i forhold til CISC arkitektur som brukes bl.a. av Intel på PC plattform.
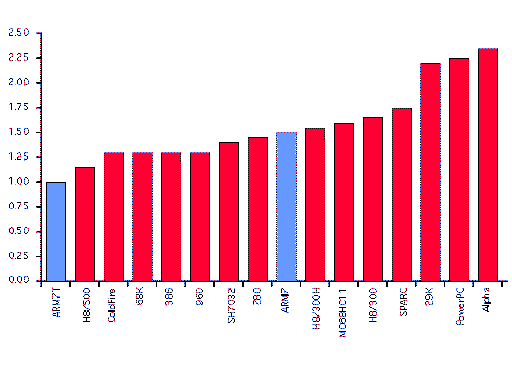
Få instruksjoner og få klokkesykler per instruksjon gjør prosessorens ytelse i forhold til klokkehastighet effektiv.
|
Table 6: Processors at 5 volts
in 16-bit memory systems Processor |
System |
Power (W) |
Ds1.1 MIPS |
MIPS/Watt |
|
ARM7TDMI |
33MHz 5V |
0.181 |
21.2 |
117 |
|
ARM7D |
33MHz 5V |
0.165 |
16.3 |
99 |
|
ARM710 |
33MHz 5V |
0.424 |
38.2 |
90 |
|
Z380 |
18 MHz |
0.04 |
3.1 |
78 |
|
SH7032 |
20MHz 5V |
0.5 |
16.4 |
33 |
|
H8/500 |
10MHz 5V |
0.1 |
1 |
10 |
|
486SLC |
33MHz 5V |
2.25 |
18 |
8 |
|
H8/300H |
16MHz 5V |
0.25 |
1.9 |
8 |
|
386SLC |
25 MHz 5V |
2.5 |
8 |
3 |
Figur 28, Sammenligning av prosessortyper og ytelse.
Prosessoren utmerker seg også ved at det kreves vesentlig mindre minne enn andre prosessorer med tilsvarende bussbredde fordi man kan benytte både 16 bit og 32 bit instruksjoner. Dette gjøres med en dekoder enhet i prosessoren. Generelt kan man si at 32 bit instruksjoner øker ytelsen og minnekravet, mens 16 bit instruksjoner senker programminnebehovet og strømforbruket.
Intel 386
Motorola Power PC
Figur 29, Sammenligning av programminne krav for forskjellige prosessorplattformer og mellom 16 bit og 32 bit instruksjoner på ARM/Thumb prosessorer.
ARM prosessor – I/O arkitektur
Parallell I/O
Prosessoren har 16 parallell ekstern databuss og 24 bit ekstern adressebuss. Bussene styres av parallell I/O kontrolleren. I vårt system er benyttes det store adresseområde for å adressere periferenhetene for ARM prosessoren, samtidig som SRAM og Flash RAM for ARM prosessoren ligger i andre deler av adresseområdet. For at lesing og skriving til og fra periferenhetene skal fungere mest mulig optimalt under C programmering og at systemet skal fungere som et konvensjonelt mikroprosessorsystem, er enhetene koblet mot ARM prosessoren tildelt minneplasser på lik linje med SRAM.
Mer om systemet i ”Multiprosessor arkitektur” og ”Komponenter i parallellbussystemet”
Seriell I/O
ARM prosessoren har 2 serieporter, dvs. 2 seriekontrollere – USART. Disse seriekontrollerne kan operere helt opp til 1 x systemklokkefrekvens, dvs. 32,768MHz ved synkron dataoverføring. Ved asynkron dataoverføring kan overføringshastigheten være opp mot 1/16 av systemklokken. Under programmering brukes den ene porten til debugger funksjoner. Den ledige serieporten blir brukt til ta i mot og sende MIDI signaler. MIDI er en asynkron seriell overføring som er standard for musikkinstrumenter.
Overføringshastigheten ligger på 31,25Kbaud, noe mikrokontrolleren klarer med god margin, bl.a. ved hjelp av den innebygde baudgeneratoren. MIDI er en duplex protokoll som krever at serieporten, USARTen, kan sende og motta samtidig. ARM prosessoren kan i likhet med de fleste moderne mikrokontrollere og prosessorer ta seg av dette.
(se mer om ”MIDI standard – elektrisk spesifikasjon” og ”MIDI standard – softwareprotokoll”).
Minne arkitektur
Intern SRAM
8Kbyte sitter inne i prosessor pakken. Dette minnet brukes til de mest brukte variablene, og som et "cache", eller korttidsminne fordi det kan operere på prosessorens klokkehastighet.
SRAM
Atmel prosessoren kan adressere opp til 64 MByte RAM. I vårt system, og for utviklingskit'et levert av Atmel, er kontrolleren konfigurert med 512 KByte SRAM. Dette minnet sitter på den eksterne adressebussen og eksterne databussen. Det tar nødvendigvis noe lengre til å skrive og lese fra dette minnet, hastigheten kan maksimalt være ½ ganger systemklokken. Den eksterne databussen har, som tidligere nevnt, 16 bits bredde, hvilket medfører at 32 biters ord må skrives i 2 sekvenser.
Flash RAM
128KByte sitter på utviklingskit'et som brukes i systemet. Dette minnet er delt i 2. Halvparten brukes under kjøring med debug støtte i hardware med Angel software. Prosessoren booter med Angel software for å kunne debugmonitor over seriekommunikasjon med PC. Den andre halvparten brukes til å boote fra når prosessoren kjører uten debugmonitor. Prosessoren booter også fra dette minnet som frittstående enhet etter at flashminnet er programmert på forhånd. Vi skifter mellom Flash minnets to deler med en bryter på prosessorkortet.
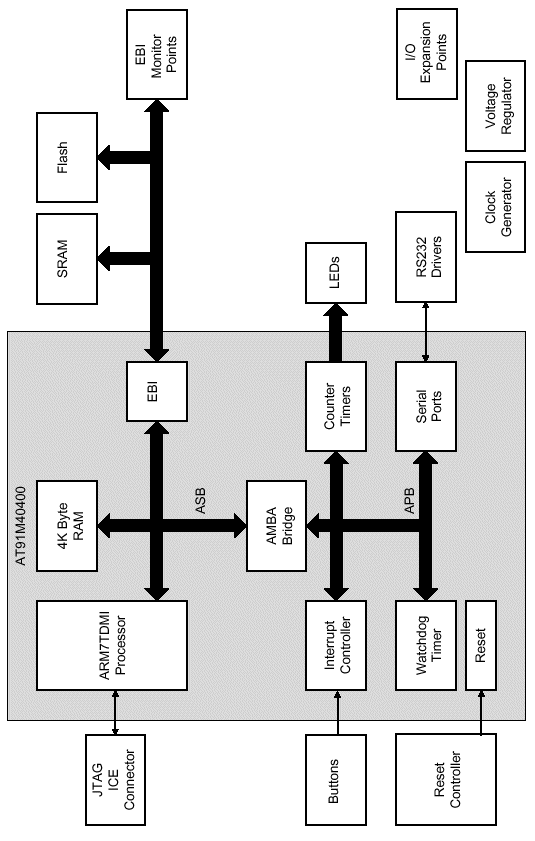
Figur30, Atmel EB01 M40400. Hentet fra EB01 User’s Manual
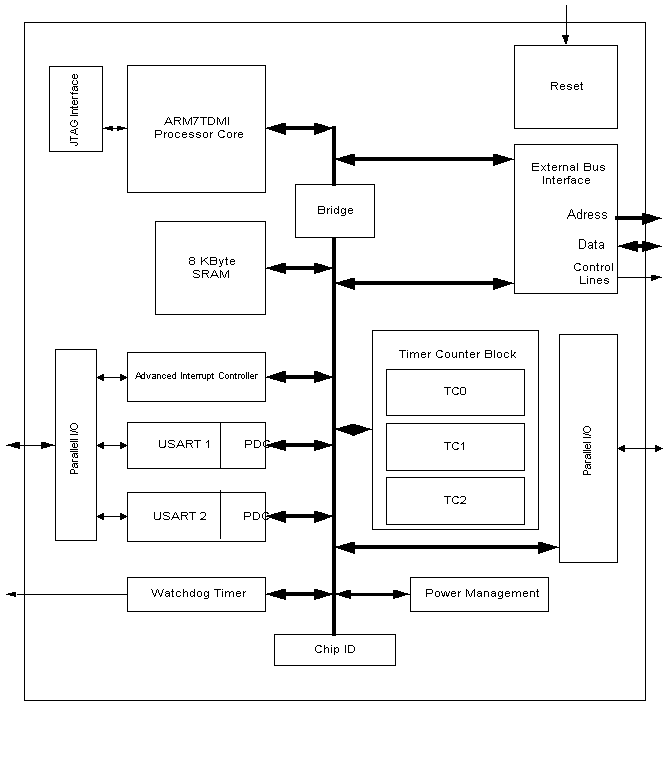Figur 31, Mikrokontrollerens indre arkitektur.
Enhetenes rolle i systemet er omtalt i kapitlet "Valg av mikrokontroller”.
Atmel prosessor - Perifer arkitektur
Atmel prosessorens oppgave er å lese inn verdier fra bruker input, behandle parameterne for deretter å sende disse til en av DSP prosessorene. Atmel prosessoren styrer også displayet og genererer grafikk og karakterer for dette. For å ta seg av oppgavene bruker vi flere periferenheter. Disse er i gruppene analog til digital konvertere, adressedekoder, vipper og bussdrivere. Atmel prosessorens eksterne minne er plassert på EB01 utviklingskit'et. Alle andre periferenheter som kommuniserer serielt eller parallelt med mikrokontrolleren skal plasseres på et egenutviklet sammenkoblingskort. En av DSP prosessorene kobles også til på sammenkoblingskortet for kommunikasjon med mikrokontrolleren over. Mer om sammenkoblingskortet under punket ”Design av kretskort for sammenkobling av kit og plassering av periferenheter” og mer om kommunikasjon mellom mikrokontroller DSP prosessor.
Multeprosessorarkitektur – Kommunikasjon med prosessor på forskjellig plattform
Atmel prosessoren og SHARC DSP prosessoren har forskjellig grensesnitt når det gjelder kommunikasjon over parallellbuss. Atmel prosessoren kan sende 16 data biter i parallell, mens DSP prosessoren kan sende data biter med opp til 32 biters bussbredde. Dette løses ved å sende og motta fra de nederste minst signifikante bitene. DSP prosessoren har støtte for denne typen kommunikasjon.
For at kommunikasjonen skal bli uavhengig av prosessorenes forskjellige asynkrone klokkehastigheter må det lages et bufferminne mellom bussene. Vi bruker 4 oktal flanketriggede D-vippe for hvor dataene legges ut før de hentes inn på den respektive prosessoren avhengig av hvilken vei dataene går.
Dataoverføringen går med en protokoll hvor overføring alltid initieres av Atmel prosessoren.
Kommunikasjonen kan går begge veier.
Det er flere muligheter for sammenkobling av Atmel og SHARC prosessorer avhengig av hvor stor kontroll mikrokontrolleren skal ha over DSP prosessoren. Hovedtypene av sammenkobling er ”External Port DMA” (EPD) og ”Host Processor Interface” (HPI).
HPI tillater en ekstern prosessor å styre SHARC prosessoren, dvs. kontrollere eksekvering av kode, og kontroll av SHARC prosessorens interne registre. Denne kontrollen gir utstrakt mulighet til og skrive og lese til prosessorens minneområde og kontrollere hvor dataene legges i SHARC minnet. Dette krever en sammenkobling av adresselinjer, datalinjer og en rekke kontrollinjer til den eksterne prosessoren. (se vedlegg: ADSP-21065L SHARC, User's Manual, Figur 7-1) HPI er relativt omfattende og krever adresselinjer og flere komponenter enn EPD.
Med EPD har ikke den eksterne prosessoren, i vårt tilfelle Atmel prosessoren, kontroll på hvor overført data legges i SHARC minnet. SHARC prosessoren bestemmer hvor data legges, og hvor data kan hentes fra, men selve overføringen initieres fra Atmel prosessoren. EPD krever færre linjer enn HPI, færre hjelpekomponenter og er enklere å implementere enn HPI både i software og hardware. EPD kan operere opp mot busshastighet på Atmel prosessoren og fungerer bra i vårt system fordi mikrokontrollerens oppgave mot DSP prosessorene i systemet er å kun overføre parameterdata til DSP prosessorenes variable. Mer om hvordan protokollen mellom Atmel og SHARC finnes i software kapittelet om ” Parameter overføring – DMA til og fra SHARC DSP”.
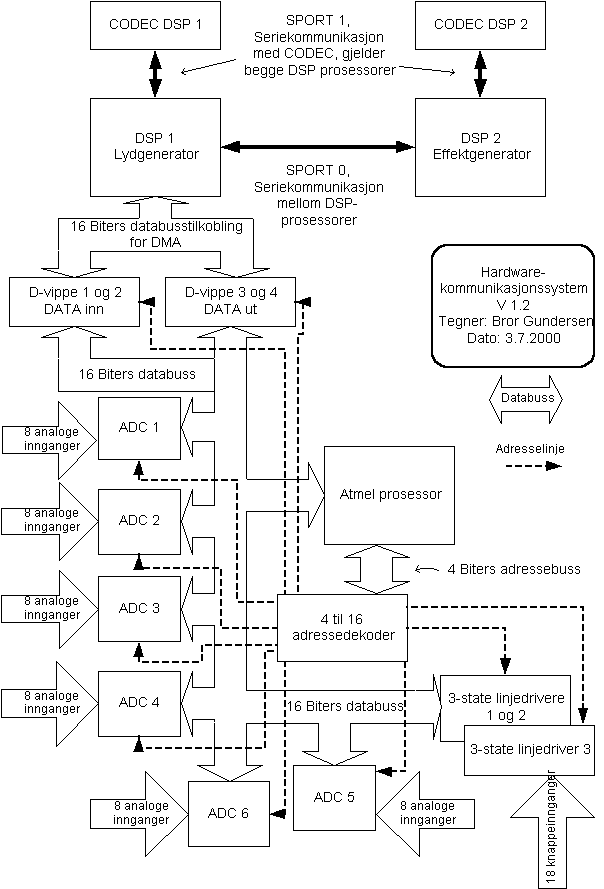
Figur 32, Systemets hardwarearkitektur og busstruktur.
Komponenter i parallellbussystemet
Analog til digital omformere (ADC) – Analog Devices AD7859
For å kunne lese inn spenningsverdier fra potensiometere på synthesizerens kontrolloverflate er det nødvendig med 48 ADC innganger. Det vil være urasjonelt å bruke 48 separate ADCer både økonomisk, plassmessig og elektrisk. Et alternativ kunne vært å bruke pulspotensiometre med uendelig vridning. Prisen per potensiometer for dette alternativet overskred den valgte løsningen med nærmere 10 ganger, og ble avskrevet av hensyn til det totale kostnadsnivået. For å få tilstrekkelig antall innganger vurderte vi forskjellige multipleksingsteknikker. Utviklingsverktøyene tilgjengelig tillot ikke utstrakt simulering av komplekse multiplekser systemer, derfor besluttet vi å velge en løsning med størst mulig forutsigbarhet og kontrollerbarhet. Det er også viktig for optimalisering av ytelsen til mikrokontrolleren at ADCen har parallell dataoverføring, og at den kan tildeles en adresse i Atmel prosessorens minneområde.
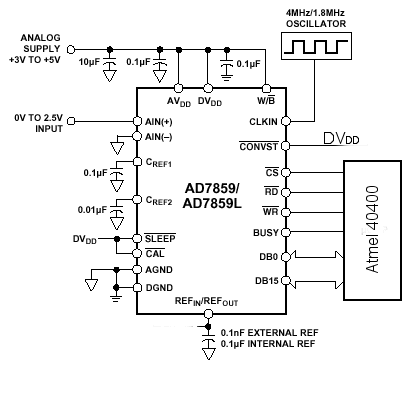
Figur 33, Analog til digital omformerens hjelpekomponenter og prosessortilkobling. Figur hentet fra AD7859 datablad, med modifikasjoner for tilpasning til vårt system.
ADCene vi valgte er softwarestyrte hvor mikrokontrolleren leser og skriver til interne registre i hver ADC. ADCene følger samme buffrede klokke, men er ikke avhengige av synkronisering seg i mellom. ADCene kan sample med opp til 200KHz. Denne høye samplingsfrekvensen minimerer behovet for antialiasingfiltere på inngangene. Utlesing av data er softwarestyrt slik at avlesingsfrekvensen kan styres softwaremessig for å tilpasse hastigheten til det aktuelle parameteren og hvor rask oppdatering som behøves.
Konverter funksjon – AD7859
Figur 34, Funksjonsdiagram AD7859
Se også datablad for AD7859/AD7859L
Referansespenning
Konverteren har Vdd = 3,3V spenningsforsyning, og inngangssignalene fra potensiometrene varierer mellom 0-3,3V minus spenningsfall i ledere. Vi har ikke tatt hensyn til variasjon i potensiometrene fordi det ikke er viktig med stor presisjon i avlesning av minimums og maksimumsutslagene bare disse holder seg innenfor 0-3,3V. Vi benytter den interne referansespenningen i konverteren. Konverteren blir internt kalibrert før konvertering starter.
Kvantisering
Dataene leses ut med 16 bit bussbredde (mer om utlesings protokollen i ”Mikrokontroller software prinsipper” kapittelet), hvor de 12 minst signifikante bitene brukes til å kode signalet. Med 3,3V som fullt utslag gir dette 3,3/(2^12) = 0,8mV per steg i konverteringen.
I vårt design har vi lagt vekt på at endring i parametere skal ”føles og høres analoge”, dvs.. at det ikke kan oppfattes diskrete nivåer ved endring i parametere som for eksempel endring i filter knekkfrekvensen eller resonanshøyden i filteret. Den høye oppløsningen skal bidra til å minke effekten av kvantisering mellom nivåer.
Det er aktuelt for senere utvidelser å implementere ”MIDI Realtime Controller” sending på ”MIDI OUT” porten. Disse sanntids kontrollsignalene kan sendes med en oppløsning på opp til 14 bit. AD7809 sampler med 12 biters oppløsning, hvilket er tilstrekkelig for parametersending over MIDI. Mer om ”MIDI Realtime Controller” og ”MIDI OUT” i softwareprinsipper.
Klokkekrets til ADC
ADCene bruker en 4MHz klokke under operasjon. Klokkesignalet hentes fra en konvensjonell krystall klokke krets laget med et krystall, kondensatorer, en ubufret inverter (74HCU04) og en oktal Schmittrigger(74HC. Schmittriggeren sørger for å lage mest mulige steile flanker på klokkepulsene, samt at den fungerer som distribusjons buffer til de 6 ADCene. Triggerinngangene er koblet på ”out” i kretsen tilsvarende ”out” i figuren under.
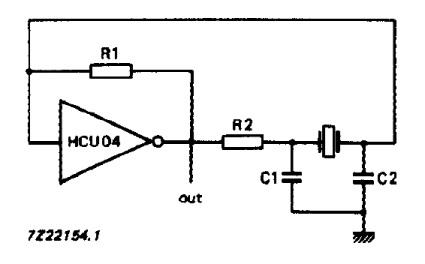
Figur 35, Klokkekrets, hentet fra 74HCU04 manual.
Display – Seiko G242C
Enhetens display skal presentere relevant informasjon for brukeren av synthesizeren om aktuelle parameterdata og brukerkonfigurasjon av DSP algoritmene. Størrelsen på displayet var av viktig karakter. Ønsket var å få et stort nok display til å kunne tegne grafikk samtidig som vi enkelt kan skrive karakterer. All grafikk og tekst må være leselig på god avstand. Vinkelen for hvor skarpt brukeren kan stå og samtidig lese displayet har betydning når brukeren ikke alltid er plassert foran displayet under bruk. Seiko G242C har 240 X 128 pixler og innebygget driver med karaktergenerator og grafikkgenerator. Display overflaten er 122,36mm X 65,24mm stor. Grafikk og tekst på G242C kan sees opp til q2 = 55° (se figur under for q2 definisjon) ut fra en akse som står 90° på displayet.
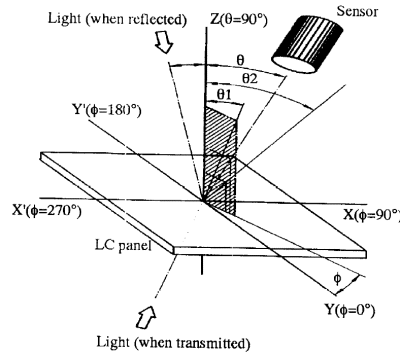
Figur 36. Definisjon av leselighetsvinkel
De forhåndsdefinerte karakterene er 5 X 7 pixler, og det er mulig å definere sine egne karakterer som kan legges i displayets minne. Det er 8Kbyte karakter RAM i displayet for egne karakterdefinisjoner.
Både for at leseligheten skal være god og at det er høyst nødvendig å kunne avlese displayet i mørke eller i dårlig lys, valgte vi å bruke et bakgrunnsbelyst display. Av hensyn til Arm prosessorens ytelse er den 8 biters databussen på Seiko displayet å foretrekke fremfor en løsning med seriell kommunikasjon. Parallellbussen gjør det også mulig å tildele displayet en minneadresse i Arm prosessorens minneområde. Bussen har et standard mikroposessorgrensesnitt med signalerings linjer for konvensjonell lesing og skriving til minnet i displayet.
Prinsipper for displayets virkemåte – prosessorkrav
Skriving av grafikk til et display krever mer ressurser enn å skrive karakterer til et rent karakterdisplay som brukes i tilsvarende applikasjoner. Skriving av grafikk til displayet foregår ved skrive 8 pixler av gangen. Det betyr at det tar (128 x 240)/8 = 3840 skrive operasjoner for å fylle displayet en gang. Fordi dette er relativt krevende må vi ta hensyn til hvor raskt vi velger å oppdatere grafikken, slik at dette ikke går ut over sanntidsytelsen til parameteroppdateringen og MIDI.
Inverter – ILP-324-INV
Som spenningsforsyning til displayet brukes en inverter levert av Seiko. Kretsen sitter på et eget kretskort med 5 V spenningsforsyning, og gir mellom 850 til 1300V AC ved 25 til 45 KHz ut til displayet.
D-vipper for DMA overføring mellom Atmel og SHARC prosessor - 74HC374
Vi bruker 4 oktal positiv flanke triggede D-vipper med 3-state utgang som buffer mellom prosessorene for å tilpasse busshastighetene som nevnt i punktet ”Multiprosessorarkitektur – Kommunikasjon med prosessor på forskjellig plattform” . Vi er avhengige av at disse latchene følger busshastigheten. Med 3,3V i forsyningsspenning valgte vi å bruke vipper i 74HC familien med typiske fall og stigetider på 1 nS. Maksimal busshastighet kan ligge opp mot Atmel klokke delt på 4, dvs.. 1/systemklokke/4 = (1/32768000Hz)/4 = 0,12 ms. Vi bruker 4 vipper for å gi totalt 32 linjer – 16 inn og 16 ut fra SHARC prosessoren (se fig. 32 for hardwarearkitektur) Vippene er tildelt adresser i Atmel prosessorens adresseområde. Mer om funksjon i punktet ” Parameter overføring – DMA til og fra SHARC DSP”. Det er viktig at utgangene som legger data ut på DSP databussen har mulighet for å settes i høyimpedant tilstand for å ikke forstyrre DSP prosessorens kommunikasjon med SRAM på DSP utviklings kitet.
Figur 37, Logikkdiagram for 74HC374
Adressedekoder – 74HC154
Vi bruker en 4 til 16 linjers adressedekoder som er koblet til de 4 øverste adresselinjene på mikrokontrolleren. Denne er med på å adressere alle mikrokontrollerens periferenheter. Denne brukes for å spare adresselinjer som brukes direkte fra mikrokontrolleren, og for å bruke adressene som ligger over adresseområdet til mikrokontrollerens eksterne SRAM. Vi bruker c-mos HC serie for å klare busshastigheten på mikrokontrollerens adressebuss som operer opp til systemklokke delt på 2 – 32,768MHz/2 = 16,384MHz. Prosessorbussene er designet med c-mos teknologi og HC serien er kompatibel med denne, og drives med 3,3V spenning for tilpasning til resten av mikrokontrollerens periferenheter. Se elektronisk vedlegg for logisk funksjonsbeskrivelse av 74HC154.
3-State linjedriver – 74HC244
Sammenkoblingskortet er utstyrt med 3 oktal 3-state bussdrivere
Denne bussdriveren skal ta i mot signaler fra knapper som sitter på synthens kontrollpanel.
Disse knappene har glitchfilter for å unngå rippel på driverinngangene. 3-state utgangene skal sørge for at mikrokontrollerens databuss ikke forstyrres av knappeaktivitet under skriving og lesing til andre enheter, samtidig som disse er adressert fra mikrokontrolleren (se vedlegg for hvordan bussdriveren er memorymappet). Vi bruker HC serie drivere for å kunne operere under full hastighet på databuss. Bussdriveren bruker 3,3V spenningsforsyning for tilpasning til mikrokontrollerens 3,3Volts busser.
Figur 38, Logikkdiagram for linjedriver 74HC244.
Komponenter for seriebuss
MIDI hardware standard
MIDI eller Musical Digital Interface er en standard for kommunikasjon mellom musikkinstrumenter. MIDI brukes til å sende enkle note beskjeder og kontrolldata til og fra MIDI bestykket utstyr. MIDI kommunikasjonen foregår med asynkron seriell dataoverføring. Inngang og utgang på kommunikasjonskanalen er adskilt, dvs.. at det er en 5 pins DIN plugg for utgang og en 5 pins DIN plugg for inngang. De fleste MIDI enheter har i tillegg en THRU utgang som er en bufret versjon av inngangen for å kunne koble sammen flere enheter i en kjede. Her er det underforstått at det kun kan kobles en enhet til per inn eller utgang for å ikke overlaste bufrene eller få andre konflikter. I den 5 pins kabelen brukes 2 ledere, en for jord og en for signal, i tillegg kan eventuell skjerm i kabel tilkobles pluggens ytre kappe i den ene enden. Det er viktig at den ytre skjermen ikke kobles til i begge ender for å unngå jordsløyfer.
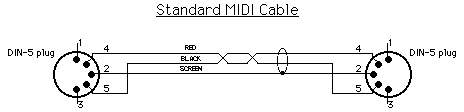
Figur 39, MIDI-kabel.
MIDI er en strømsløyfe med 5mA og 5V som logisk 0 og jord som logisk 1. Overføringshastigheten er 31,25 Kbaud +/- 1%, og er i vår applikasjon koblet videre til en av serieportene på mikrokontrolleren. Det overføres et bit per klokkepuls. MIDI signalene er kodet i byter, men for å sikre stabilitet i overføringen har byten et startbit og et stoppbit, m.a.o. 10 biter totalt. Atmel prosessoren har innebygget seriekontroller som generer riktig baudrate, samtidig som den tar seg av synkroniseringen av datamottak, samt fjerning av start og stopp bit. MIDI-trafikken på bussen er hendelsesavhengig.
Se mer om MIDI software protokoll spesifikasjon i softwareprinsipper og i det elektroniske vedlegget.
MIDI krets
Vi følger i hovedsak prinsippene for en standard MIDI krets som er anbefalt av MIDI Manufacturers Association, med noen få endringer for å tilpasse MIDI IN til 3,3V serieport på Atmelprosessoren. Vi har også valgt å bruke en annen inverter som bl.a. har c-mos kompatible innganger (www.midi.org for anbefalte spesifikasjoner av MMA).
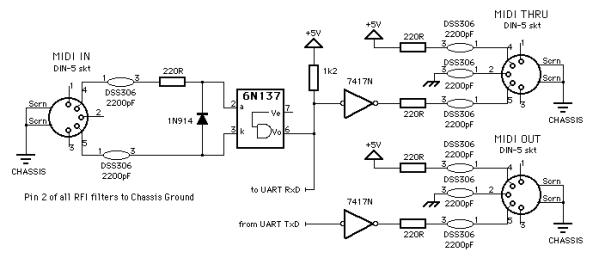
Figur 40, MIDI-krets
MIDI IN og MIDI THRU
Inngangen er optoisolert med en 6N139 for å unngå jordsløyfer i signaljord. Det er viktig å merke seg at signaljord ikke er koblet til felles jord på kretskortet eller på annen måte. Det sitter også en diode i parallell med signalveien som fungerer som ”gnistfanger”, dvs.. for å unngå store spenninger inn på optokobleren i motsatt vei av driftsområdet. MIDI-signalet er som tidligere nevnt invers kodet med logisk 0 = 5V og 1 = 0V, derfor brukes en pullupmotstand på sekundærsiden for å invertere signalet for tilpasning til seriekontrolleren som har logisk 1 = 3,3V og 0 = 0V. Optokobleren har 3,3V forsyningsspenning i vår konstruksjon for å senke spenningen til seriebusskompatibel spenning. Seriebussen tåler maksimalt 4V (se ”40400 errata” i elektronisk vedlegg)
Sekundærsiden er videre koblet til en 7407 inverter og til MIDI THRU for å kunne sende MIDI-signalet til en ny enhet i en kjede, uten at signalet er modifisert av vertsenheten. Det sitter RC serie filtre med komponentverdier R = 220 Ohm og C = 2200pF på alle tilkoblinger. Dette høypassfilteret skal hjelpe til med å fjerne lavfrekvente komponenter som nettstøy og DC. Filteret har knekkfrekvens ved 1/RC = 1/(2200e-9 * 220) = 2066 radianer = 329Hz. Det vil si at man fjerner deler av 5 harmoniske komponenter fra 50Hz nettfrekvens, i tillegg til andre støykilder med lavfrekvente og ofte energirike frekvenskomponenter.
MIDI OUT
Send kanalen på seriekontroller 1 brukes for å sende data fra vertsenheten. Dataene som passerer ut på denne kanalen går til en inverter før den sendes ut på porten, dvs.. tilkoblingen. Det er kun data fra selve synthesizeren som sendes ut på porten og ingen av dataene som kommer inn på MIDI IN. De samme RC leddene som finnes på MIDI IN og THRU sitter også på MIDI ut delen av MIDI-kretsen. Se punktet MIDI OUT og MIDI THRU for forklaring av filtrenes misjon.
Design av kretskort for sammenkobling av kit og plassering av periferenheter
Komponentene omtalt i kapittelet ”Atmel prosessor - Perifer arkitektur” skal plasseres på et eget designet kort bort sett fra displayet som er plassert på et ferdig kort levert av Seiko. Kortet er designet med Traxedit og legges ut på HiO IU.
Det er en rekke hensyn å ta for å legge ut et sammenkoblingskort for mikrokontrollerbuss. Kortet skal legges ut på et 2 lags prototypekort. Prinsippene for utlegg av sammenkoblingskortet, som er beskrevet i punktene under, er idealiserte og ikke 100% realiserbare innenfor de begrensninger et 2 lags kort gir. Dette er det nærmere redegjort for på s. XX. Se elektronisk vedlegg for kretskortutlegg.
Bussdesign
Sentralt på sammenkoblingskortet er Atmel prosessorens databuss og adressebuss. Hastigheten på bussene kan ligge opp til halvparten av Atmel prosessorens klokkehastighet, dvs.. 32,768MHz/2 = 16,384MHz. Den raske svitsjingen på bussen kan føre til problemer med støy som både virker inn på komponenter og andre linjer på kortet i tillegg til at strålingen kan virke på elektronisk utstyr på utsiden av synthesizeren. For å begrense crosstalk på kortet, er del konstruksjonene plassert mest mulig adskilt på kortet. MIDI kretsen som operer på en langt lavere klokkefrekvens enn Atmel bussene er plassert på et eget område. DSP – Atmel kommunikasjonen foregår på den ene siden av Atmel busstilkoblingen, mens analog til digital omformerne er plassert på den andre.
Linjeekvivalens
Når signaler skifter med høy frekvens må man betrakte signalene som radiobølger, hvilket medfører at man må ta hensyn til bølgeteori i tillegg til de elektriske spesifikasjonene. Banene på kretskortet har kapasitive og induktive egenskaper. Overflater med avstand mellom seg har kapasitiv spenning mellom seg. For klokke og bussignalene i vår konstruksjon virker kapasitansen som filter som forlenger logikktransisjonstiden. C-mos komponentene har en maksimum transisjonstid som ikke må overskrides hvis systemet skal operere stabilt. På sammenkoblingskortet har banene minst mulig bredde og gjennomføringene minst mulig dimensjon for å gjøre overflatene små, og dermed flatene i den kapasitive koblingen minst mulig. For å få færrest mulig kapasitive koblinger, har hver bane færrest mulig gjennomføringer.
Når det fullstendige hardware systemet skulle settes opp måtte vi sette oss ned med de komponentene vi valgte ut for å se om de lot seg gjøre å lage et funksjonelt system ut av dem.
Et problem var at vi ikke på forhånd visste hvor mye prosesseringskraft vil ville trenge for de forskjellig programvare blokkene. Vi tok en titt under panseret på en NordLead, og konstaterte at den kun brukte en Motorola DSP56302. Ved å ta en liten kikk på blokkskjemaet til denne synhten ser vi at det består av relativt få blokker og ingen effekter. Siden den algoritmen vi hadde tenkt å implementere besto av flere blokker og i tillegg effekter, regnet vi med at den ville bli tyngre for prosessoren. I tillegg til dette er ingen av oss noen kunstnere når det gjelder programmering og kommer sannsynligvis til å lage en lite effektiv kode.
Etter ”føre var” prinsippet og et raskt overslag (klokkehastighet/fs) Fant vi ut at det ville være fornuftig å bruke 2 DSP enheter, en for lyd generering og en for effekter.
Et problem som da umiddelbar meldte seg var hvordan vi skulle kople mikrokontrolleren og de to DSP prosessorene sammen i tillegg til hvordan vil skulle hente inn informasjon fra skruknappene.
Mikrokontroller – software prinsipper
Mikrokontroller softwaren skal kombinere kommunikasjon med periferenhetene samtidig som det foretas omregning og sortering av parametere. Det er viktig at softwaren bevarer sanntidskravene som kreves for at parametere oppdateres i tilstrekkelig tid slik at det ikke kan oppfattes uregelmessigheter i lydgjengivelsen. Det er generelt viktig at programflyten er kontinuerlig og ikke ender i tidkrevende venteløkker.
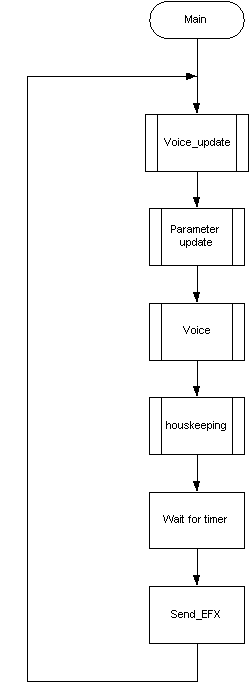
Hovedmetode – main()
Main metoden er planlagt slik at flyten i hovedprogrammet bevares. Det brukes hardwareinterrupt for hendelsbaserte programdeler som MIDI mottak på serieporten.
Hardwareinterrupt brukes også når prosessoren venter på å sende data til DSP prosessoren.
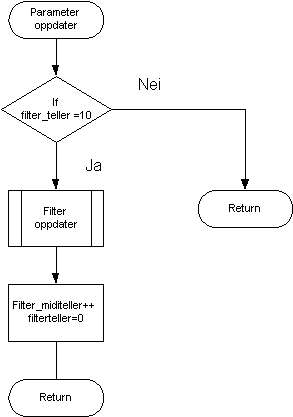
Figur 41, Hovedflyt i Atmelprogram
main() programmflyt.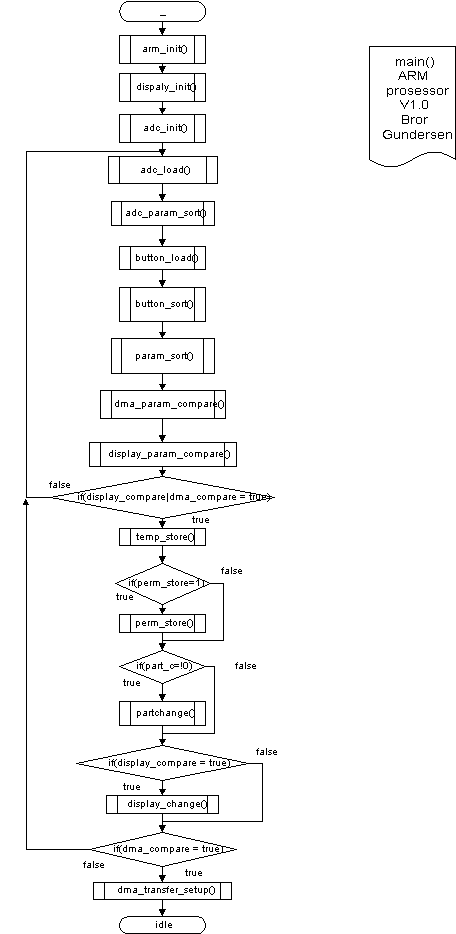
Innlesing av analog til digital konverter data
Alle potensiometere som er plassert på kontrolloverflaten blir lest inn av 6 analog til digitalkonvertere hver med 8 innganger, til sammen 48 parametere. Disse parametrene blir lest av i en sekvens hvor en adresse blir lest 8 ganger før neste adresse leses (adressebeskrivelse se vedlegget). Dette gjentas 6 ganger til alle parametere er avlest. Før avlesingsrutinen, adc_load(), startes settes ADCene opp til konvertering med en adc_init() metode og gjøres klare til opplasting av data.
Når løkken med 48 avleste verdier er ferdige, sammenlignes alle parametere med den forrige avleste verdien. Hvis verdien avviker fra den forrige, oppdateres parameteren i et DMA buffer. Bufferet sendes så til DSP prosessoren i sin helhet. Se mer under ”Parameter overføring – DMA til og fra SHARC DSP.
Innlesing av knappeverdier
Innlesing av knappeverdier foregår ved avlesing av 2 adresser i prosessorens minneområde. For spesifikasjon av adresser se ”definisjon av knappekonfigurasjon” vedlegg. Knappeverdiene sorteres og sammenlignes med forrige verdi. Hvis verdien avviker fra forrige innleste, oppdateres bufferet for sending av parametere over DMA. Parametrene sendes til DSP prosessoren sammen med resten av verdiene som ligger i DMA bufferet.
Parameter overføring – DMA til og fra SHARC DSP
Innleste knappeverdier, potmeter verdier og MIDI data som er relevante for DSP prosessoren blir sendt som en tabell over til SHARC prosessoren. Tabellen sendes kun når det er endring i en eller flere variable. DMA overføringen foregår ved at Atmel prosessoren initierer en DMA overføring til DSP. Det er kun DSP prosessoren som har støtte for DMA. DSP prosessoren skriver til eller leser fra et fast definert minneområde som er satt opp i SHARC DMA kontrolleren. Fra Atmelprosessoren side foregår overføringen med skriving og lesing fra 2 forskjellige minneområder som tilsvarer D-vippene mellom prosessorene. Signaleringen mellom prosessorene foregår ved at hver gang det skrives eller leses fra en vippe sendes det samtidig en forespørsel til DSP prosessoren om overføring. Når forespørselen bekreftes starter dette signalet en av to avbruddsrutiner på mikrokontrolleren, avhengig om det skal leses eller skrives. Avbruddsrutinen fullfører overføringen, og starter skrivingen av neste verdi i tabellen. Dette gjentar seg til hele buffer tabellen er skrevet eller lest. Adressedefinisjon finnes i memorymapping definisjonen i kodevedlegget.
MIDI
MIDI protokoll
MIDI software protokollen skal utveksle data mellom forskjellige MIDI bestykkede enheter. Det kan dreie seg om kommunikasjon mellom forskjellige enheter som f.eks. vist i figuren under.
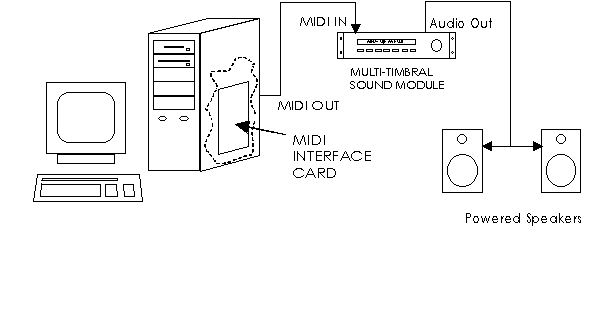
Figur 42. MIDI system hentet fra MMA
Hensikt med MIDI
MIDI er enkle meldinger som overfører note informasjon, kontrollmeldinger til og fra MIDI enhetene, systeminformasjon til og fra MIDI enhetene og sanntidskontroll meldinger. MIDI kan overføre samplinger, men dette er ikke i sanntid, og ytelsen er så dårlig at det sjelden er aktuelt. Over MIDI vil 10 sekunder med lyd i mono, 16 bits oppløsning og 44,1KHz samplingsfrekvens bruke (44100 x 10 x 16/2)/31250 = 28,224 sekunder, i tillegg kommer andre systemsignaler. Erfaringsmessig bruker overføringen lengre tid. Det finnes andre løsninger for dette på markedet som bruker ca 1/10 eller mindre tid.
MIDI koding
MIDI informasjonen er representert i byter dvs.. 8 bit. Den første biten brukes til å angi om informasjonen er en statusbyte eller en databyte. Det betyr at det er 7 bit til å kode resten av informasjonen, hvilket gir 127 kombinasjoner. For enkelte sanntidskontrollparametere brukes to og to byter til å kode informasjonen, dette gir til sammen 14 biters oppløsning, hvilket gir 16384 nivåer. Et eksempel på dette er ”Pitch Wheel”, eller tonehjul, som kan brukes til å øke eller senke frekvensen uten at man hører de diskrete nivåene mens man skifter opp og ned.
Vi går ikke nærmere inn på spesifikasjonen av alle forskjellige MIDI data definisjonene, mer om dette finnes i det elektroniske vedlegget under ”MIDI 1.0 Spesifikasjon MMA”.
MIDI protokollbeskrivelse
MIDI protokollen består som tidligere nevnt av statusbyter og databyter. Generelt gjelder det at en sekvens av data starter alltid med et statusbyte. Deretter følger 0,1,2 eller et ubestemt antall databyter, avhengig av hva slags statusbyte som kom først i sekvensen. Statusbytene deles opp i 2 nibbels som forteller hva slags type MIDI parameter det er snakk om. Mer om protokollen i det elektroniske vedlegget under ”MIDI 1.0 Spesifikasjon MMA”.
MIDI algoritme
I den første versjonen av vår MIDI algoritme har vi konsentrert oss om note på, ”note on” og note av, ”note off”. Note on og note off kan sendes til 16 forskjellige instrumentlyder med 127 forskjellige noteverdier til hver av instrumentene. Det er forhåndsdefinert i DSP software hvilken instrumentkanal noteverdier tas i mot på. MIDI algoritmen i mikrokontrolleren har som oppgave å sende instrument nummer og notenummer sammen med note på eller av for den respektive noten. Informasjonen sendes som en del av DMA parameter tabellen. I DMA tabellen settes bit som forteller om det finnes ny MIDI informasjon som ennå ikke er lest og hva slags type ny MIDI byte som sendes.
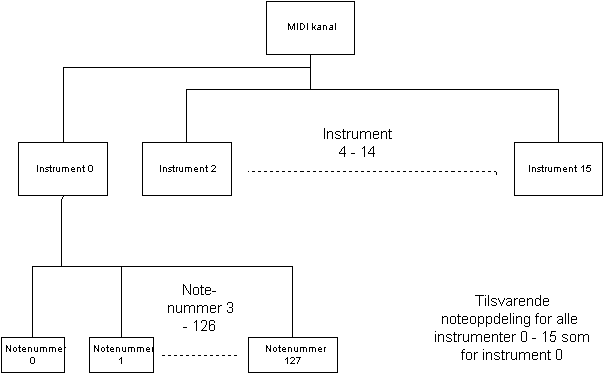
Figur 43 , Inndeling av midinoter, instrumenter i forhold til kanal
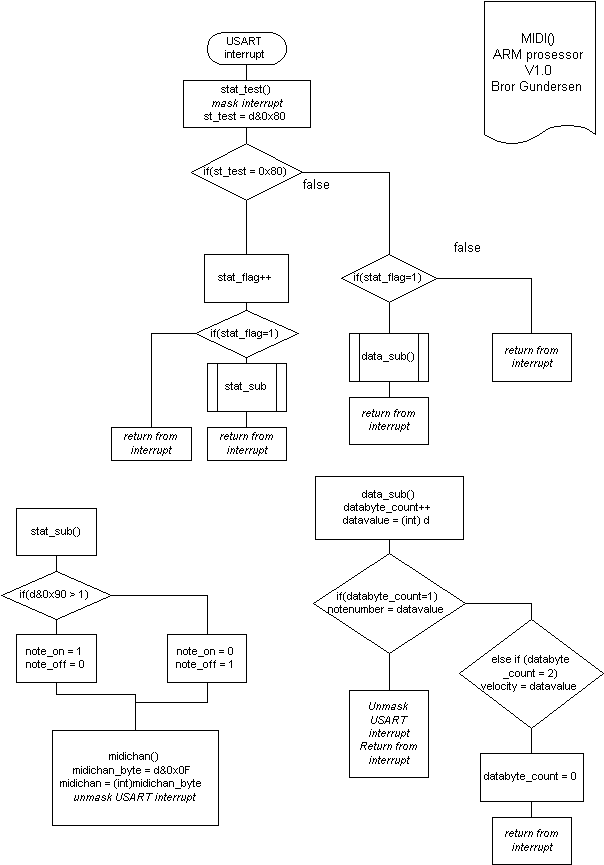
Figur 44, Programflyt i MIDI algoritme
Display
Det er ikke utviklet metoder for displaykommunikasjon.
Lyd-Blokkene –DSP prosessor
Sammen med EZ-LAB fulgte det med et utviklingsmiljø som heter VisualDSP, dette var riktignok en demo versjon med 60 dagers lisens, men passet bra til vårt formål. VisualDSP har både en Assembler og en C kompilator. Siden C er et litt mer oversiktlig og lettskrevet språk enn Assembler valgte vi å satse på det i utgangspunktet.
VisualDSP sin C kompilator er en omskrivning av den kjente Gnu C Compiler (GCC) for Analog sine signal prosessorer. Denne kompilatoren støtter derfor standard ANSI C funksjoner i tillegg til spesialskrevne signalbehandlings bibliotek fra Analog.
Med tanke på selve utviklingsprosessen valgte vi å først implementere funksjonen til hver enkelt blokk hver for seg for så til slutt å integrere dem i en komplet algoritme.
Siden baktanken med disse blokkene er å bruke de i en sanntids algoritme må stort sett alle variablene være globale slik at de kan oppdateres av mikrokontrolleren. Funksjonene tar derfor ikke imot signaler direkte eller returner noe, men oppdaterer eksisterende variabler.
OSC
Oscillatoren er grunnblokken i en subtraktiv algoritme. Som nevnt tidligere må denne inneholde et rikt harmonisk spekter. Firkant og trekant bølger egner seg derfor ypperlig til dette siden de inneholder en rekke harmoniske komponenter.
Rent teknisk må vi forholde oss til at punktprøvingsfrekvensen er fast 48kHz, altså 48000 punktprøver i sekundet. For å finne ut periode tiden bruker vi formelen
periode =
punktprøvefrekvens/ønsket firkantbølge frekvens
For at frekvensen skal kunne varieres i sanntid må funksjonen lese frekvens, og for hvert sample inkrementere en teller slik at bølgeformen kan genereres.
Firkant bølge
En firkant puls har en ganske enkel struktur å programmere siden den er 1 i halve periodetiden og –1 i resten.
Ved å definere variabelen halv_periode kan vi generere en firkant puls på følgende måte:
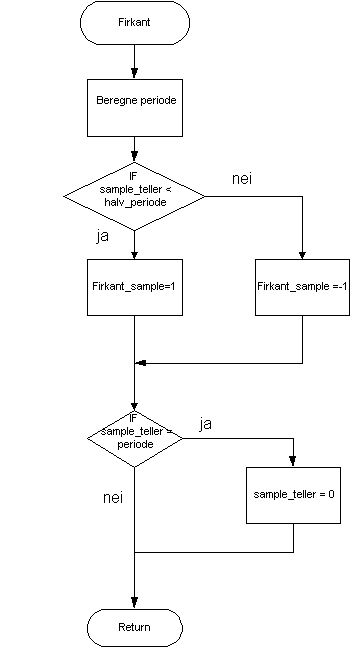
Figur 45, Firkantbølge programflyt
Sagtann bølge
En sagtann puls kalles ofte en rampe fordi den stiger jevnt fra ett nivå til et annet. Ved å la sagtann pulsen gå fra –1 til 1, defineres stigningstallet for flanken som
2*sample_teller/periode –1
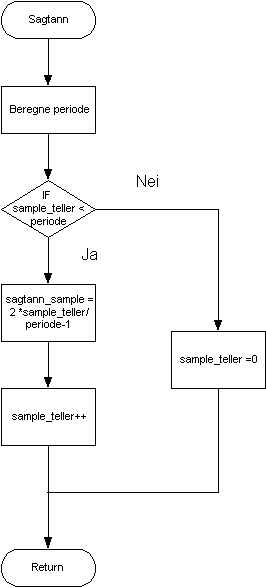
Figur 46, Sagtannbølge programflyt
LFO
En LFO er en oscillator med lav frekvens, ofte mellom 0 og 20Hz. Denne brukes som et kontroll signal i andre blokker. Ved analoge synther er LFO ofte av en sinus kurve. Det å generere en sinus med en DSP krever faktisk en del prosessorkraft. Ved å slå opp på side 1-3 i C runtime Library Manual ser vi at en sinus funksjon bruker 45 klokkepulser.
Vi valgte derfor på bruke en trekant bølge istedenfor en sinus. En trekantbølge er enkel å implementere og siden LFO kun brukes som kontrollsignal vil funksjonaliteten omtrent bli den samme. Implementasjonen av en trekantbølge er en blanding av en firkantbølge og en sagtannbølge. Trekantbølgen starter ved –1 for å øke lineært opp til 1, for deretter å minke lineært til –1 igjen. Akkurat som oscillatorene må denne blokken ta frekvens som input.
. 
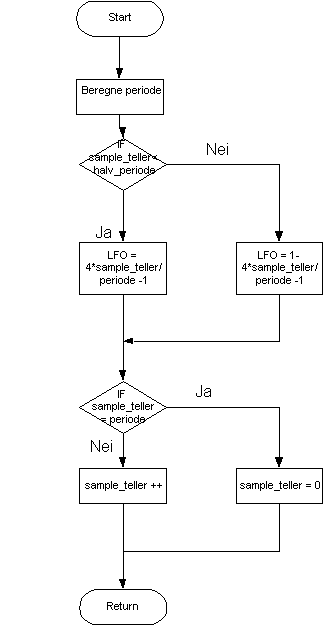
Figur 47, Programflyt LFO
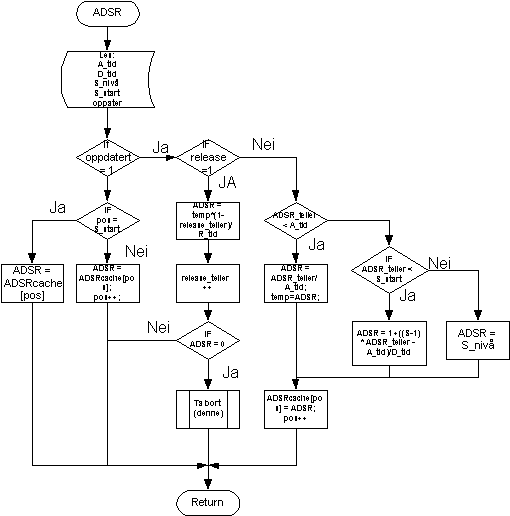
Omhylningskurver
Omhylningskurver er en del mer avanserte enn oscillatorer. En stor forskjell er at omhylningskurver ikke er repetitive slik som oscillatorene. Se ADSR figur.
Omhylningskurven må lese A_tid, D_tid, S_nivå og R_tid slik at disse parametrene er tilgjenglige for brukeren. Hvis disse parameterne ikke er oppdatert leses kurve formen ut av et hurtiglager (cache). Hvis parametrene oppdateres også hurtigbufferet.
Figur 48, programflyt ADSR omhylningskurve
FILTER
Filter blokken er den mest kompliserte funksjonen å implementere. Det største problemet med å implementere denne blokken er at brukeren skal kunne sveipe filteret opp og ned i frekvens i tillegg til å kunne justere resonans toppen i sanntid. Det er også ønskelig å kunne forandre ordenen på filteret. Her er det riktignok ikke så stort krav til sanntids responsen.
Siden filtre er noe av de mest brukte signalbehandlings teknikkene har Analog Devices laget en egen IIR() funksjon i C. Denne tar seg av selve filter algoritmen og iterasjonen av koeffisientene. Vi som brukere må riktignok levere to tabeller med teller og nevnerpolynomets koeffisienter. Disse koeffisientene skal være på den bestemt form som kalles Oppenheim&Schaefer Transposed FormII. Dette er en vri på den kanoniske blokkframstillingen vi var inne på tidligere i oppgaven. Dette har kun med rekkefølgen på koeffisientene legges inn i tabellen å gjøre.
Vi startet med å bruke Billineær transformasjon på et analogt filter. Hensikten med dette var at vi da kunne emulere et høyere ordens filter med mulighet for frekvens sveip og resonans variasjon ved å justere de analoge komponent verdiene.
Det viste seg imidlertid at dette fungerte svært dårlig, trolig av flere årsaker. Den mest åpenbare var at vi ikke hadde kontroll på filterets stabilitet. Det ble ustabilt og derfor helt ubrukelig.
Da vi endelig fattet dette forsøkte vi med Pol og nullpunkts plassering.
En liten nøtt var fortsatt hvordan vi skulle løse problemet med sveipbar frekvens og resonans. Vi kom til slutt fram til at vi måtte generere alle mulige pol plasseringer på forhånd og legge dem inn i en flerdimensjonal tabell. Frekvens og resonans kontrollsignalene kunne da fungere som en indeks for denne tabellen. Hvis vi valgte sammenfallende poler hos filtrene av høyere orden slapp vi også unna med kun en felles tabell.
Det filter algoritmen derfor må gjøre er å først generere alle pol plasseringene. Dette blir gjort kun en gang ved programstart og bør ikke være med i hovedprogramsløyfen. Deretter legges polene inn i en tabell. Funksjonen må i tillegg til frekvens og resonans ta orden som input signal.
Orden avgjør hvordan koeffisientene skal genereres. Når det er gjort må de ferdige koeffisientene legges inn i hver sin tabell slik at IIR() funksjonen kan benytte seg av dem.
For et 2.orden lavpass filterets overførings funksjon på formen :
Ved å løse tellerpolynomet får vi to sammenfallende nullpunkt ved ±Õ, altså en dempning for frekvensen rundt fs/2
Ved å løse nevner polynomet =0 får vi alltid to komplekskonjugerte poler.
Figur 49, Pol plassering
Ved å ta en tilfeldig kompleks verdi inne i enhetsirkelen kan man regne seg tilbake til nevner polynomet ved :
Hvor:
og
I tillegg til A og B koeffisientene må det beregnes en forsterknings konstant slik at filteret får en forsterkning lik 1 ved 0Hz. Dette kalles enhetsforsterkning og finnes ved å sette Z = 1 overføringsfunksjonen. Denne konstanten G finnes derfor ved :
Den komplette overføringsfunksjonen blir nå :
Hvis man ønsker et filter av lik orden kan man opphøye overføringsfunksjonen til ønsket orden –2. Hvis man derfor ønsker et 4.ordens filter blir dette:
På grunnlag av disse funksjonene kan det lages en algoritme som generer 2.ordens koeffisientene.
Vi valgte å lage to separate funksjoner. En som genererer 2.ordens koeffisientene A, B og G, og en som på grunnlag av disse beregner filterets overføringsfunksjon i ønsket orden og lager filter koeffisient tabellene til IIR() funksjonen.
Vi måtte bestemme oss for en filteroppløsning. Denne tabellen blir ganske stor og kan beregnes ved:
Tabellstørrelse = frekvensoppløsning * resonansoppløsning * 3
Ved å bruke en 256 nivåer ender vi opp med en tabell som er 196kB stor, som vi får plass til i minnet.
Filterbank funksjonen kan beskrives som:
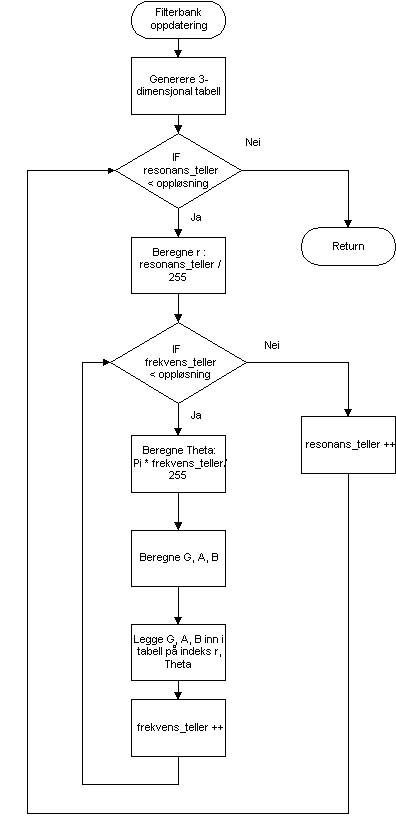
Figur 50, Filterbank programflyt.
Den andre funksjonen tar seg av selve koeffisient oppdateringen. Denne må kjøres hver gang brukeren justerer frekvens, resonans eller orden og ser slik ut:
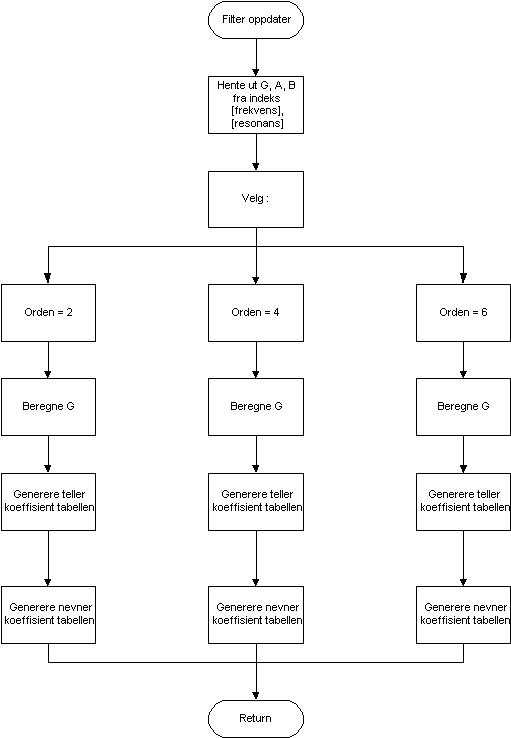
Figur 51, Koeffisientoppdatering.
Samplene kan nå filtreres ved å kalle denne funksjonen:
Figur 52, Filterkall
Panorering
Panorering vil si at en lyds posisjon kan variere fra helt til venstre og helt til høyre i lydbildet.
Dette kan gjøres fysisk korrekt med tanke på oppfattet lydstyrke, ved hjelp av vektor beregninger.
Siden vi kun vi kun er interessert i å implementere funksjonen bruker vi kun en enklere løsning med en panorerings konstant slik at :
Venstre_kanal = mono_sample*pan ..og Høyre_kanal = mono_sample*(1-pan)
Vi
vil nå kunne justere lydens plass i stereobildet, selv om lyden vil oppfattes
litt høyere i midten enn ute på sidene. Som et resultat av denne funksjonen
ender vi oppå med teten venstre og en høyre audio kanal. Blokkskjematisk ser
denne funksjonen slik ut :
Figur 53, Programflyt panorering.
OSC modulasjon
Pulsbredde modulasjon, PWM
Ved å gjøre matematiske funksjoner på oscillatoren vil vi oppnå å få nye og spennende frekvens spektre.
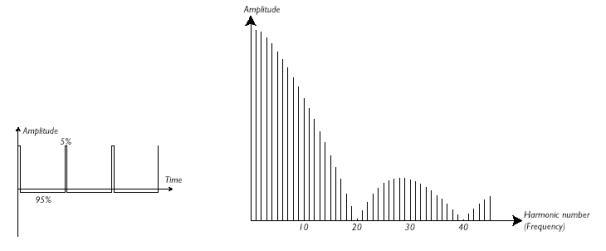
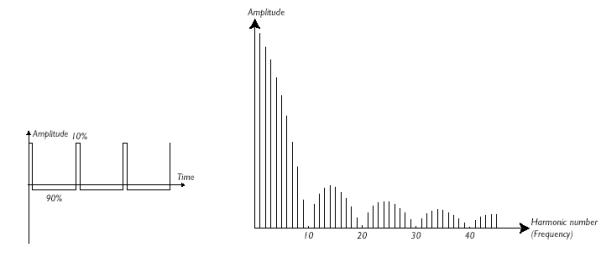
Figur 54, Pulsbreddemodulasjon av firkant som forandrer de harmoniske komponentene, figur hentet fra Clavia Nordlead brukermanual.
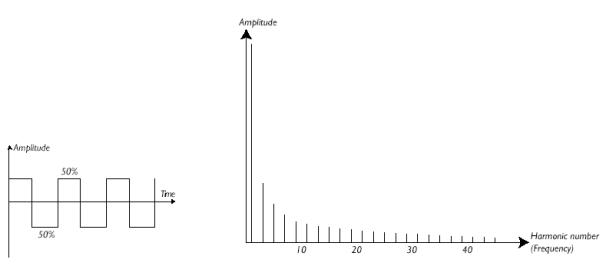
Figur 55, Firkant spekter, hentet fra NordLead brukermanual
Pulsbredde modulasjon baserer seg på den vanlige firkantbølgen. Ved å forandre forholdet mellom en periodes positive og negative del oppnåes en forandring i frekvens spekteret.
Figurene nedenfor viser forskjellige pulsbreddeforhold og deres respektive frekvens spektre.
Måten PWM kan implementeres er ganske enkelt at halv_periode pekeren som brukes i firkant oscillator funksjonen, kan varieres. Firkant oscillator funksjonen må derfor utvides med en variabel PWM konstant.
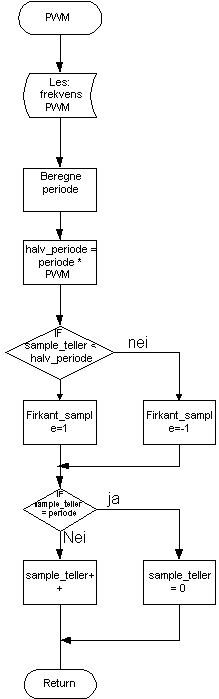
Figur 56, programflyt pulsbreddemodulasjon.
Støy
Støy
er bedre kjent som sus kan defineres som tilfeldige signalstyrker ved
tilfeldige frekvenser. Det finnes flere typer støy. Hvit støy er den vanligste
og har gjennomsnittlig like stort energi innhold for alle frekvenser. Det
finnes andre typer som er filtrerte og som derfor har høyere energi innhold for
noen frekvenser.
Det å lage totalt tilfeldige signaler er ikke helt lett ved digitale systemer. Når vi skulle implementere støy var vi tvunget til å benytte en såkalt pseudo-tilfeldig funksjon. Årsaken til at det kalles pseudo-tilfeldig er at verdiene bergenes ut fra en algoritme. Det vil si at hvis funksjonen gjentas en annen gang med det samme utgangspunktet vil man få samme svar.
Utgangspunktet er det som kalles en frø-verdi, eller seed på engelsk.
Vi vil derfor sannsynligvis ikke få riktig hvit støy i vår implementasjon.
Det finnes en egen funksjon fra Analog som generer slike tilfeldige verdier. Denne kalles rand(). Ved å sende med et heltall når funksjonen kalles kan frø-verdien forandres.
Støy lar seg derfor enkelt implementere ved:
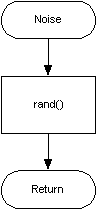
Figur 57, random kall i støyalgoritmen
Frekvens modulasjon
Frekvens modulasjon kan beskrives matematisk som
Kort forklart gå FM ut på at amplituden på et signal gir en økning eller minkning av frekvensen på et annet. Graden av hvor mye modulator signalet skal forandre bærebølge signalet kalles modulasjons graden, og benevnes som modulasjons indeksen, D.
FM gir en et rikt harmonisk spektrum som resulterer i en noe metallisk lyd karakter.
Vi valgte å bruke sagtann oscillatoren som modulator og firkant oscillatoren som bærebølge.
For å få en forandring i frekvens forandres perioden på firkant oscillatoren.
For å få en musikalsk effekt lar vi modulasjonsgraden gå i antall oktaver, altså doblinger og halveringer av grunnfrekvensen. Til dette benytter vi spesialfunksjonen ldexpf som multipliserer et tall med 2^n.
For å få en økning i frekvens må perioden divideres med D, og for å få en reduksjon i frekvens må perioden multipliseres med D.
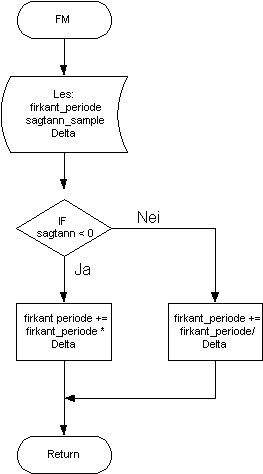
Figur 58, Programflyt – Frekvensmodulasjon.
Amplitude Modulasjon
AM er en tilsvarende modulasjons metode som FM, bortsett fra at ved AM er det amplituden som blir modulert. Matematisk fungerer AM slik:
Ved å sette modulasjonsgraden til 100% oppstår det som kalles ring modulasjon.
Lyden av et ring modulert signal kan minne litt om FM siden det gir en litt metallisk klang.
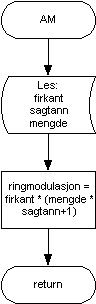
Figur 59, Programflyt – amplitudemodulasjon.
Effekter
Effekter er forskjellige prosesser som lyden gjennomgår uavhengig av syntese teknikken.
Vanlige lyd effekter er Ekko(Delay), Romklang (Reverb) og Koring (Chorus).
Ekko
Ekko effekten er kun en forsinkelse av signalet. Det er vanlig å ha flere forsinkelse elementer etter hverandre slik at forsinkelser av forskjellige lengder kan benyttes.
Dette implementeres enkelt på 21065L prosessoren siden den benytter sirkulær adressering.
For å sette opp et slikt sirkulært buffer brukes ferdige makro funksjoner fra Analog. Ved å leses eller skive til bufferet oppdateres automatisk pekerne.
Maksimal forsinkelse tid bestemmer størrelsen på bufferet. 1 sekunds forsinkelse krever 48kB i mono. Vi valgte 3 sekunder og derav totalt 288kB minne med to kanaler.
For å implementere forskjellige forsinkelse tider ved et sirkulært buffer må man definere flere pekere til bufferet. For å oppnå spennende panorerings effekter valgte vi å legge inn panorering ved hver tapning i bufferet i tillegg til en tilbakekoplings del.
Blokk skjemaet for en Ekko algoritme viser for en kanal. Den andre kanalen er identisk bortsett fra Pan parameteren.
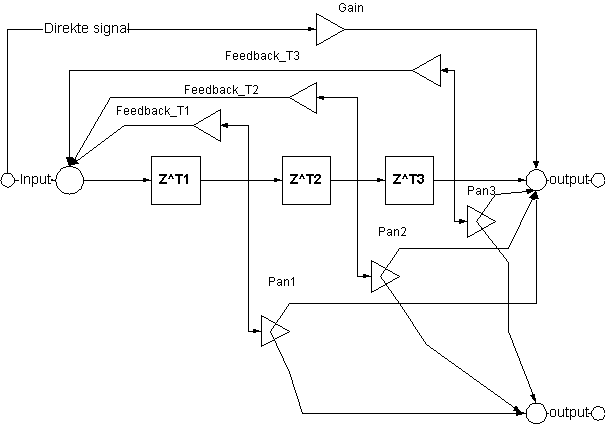
Figur 60, Blokkskjema Ekko funksjon
Figur 61, Programflyt – Ekko algoritme
Koring effekt
Koring, eller Chorus, er måte å emulere flere lydkilder, derav navnet. Måten dette fungerer er å definere en Ekko funksjon hvor forsinkelse tiden og forsinkelse forsterkningen moduleres av et tilfeldig signal..
Denne funksjonen benytter derfor rand() funksjonen for å modifiserer forsinkelese pekeren og forsterkningen. Hvis det ønskes kraftigere kor brukes flere tapninger. Denne funksjonen har ellers mye til felles med Ekko funksjonen. Under følger en blokkimplementasjon av Koring funksjonen.
Flytdiagram for Koring:
Figur 62, Programflyt - Koring
Reverb
Romklang, eller reverberasjon er en meget avansert form for Ekko og forsøker å emulere den gjenklangen som oppstår i begrensede rom, slik som kirker og konserthaller. Slike algoritmer emulerer refleksjonene som oppstår i slike rom. Disse refleksjonene deles inn i tidlige refleksjoner som er direkte refleksjoner, og etter-refleksjoner som er 2. Og 3.reflekjsoner fra vegger, gulv og tak. Figuren under illustrer dette:
Fig. Reverb
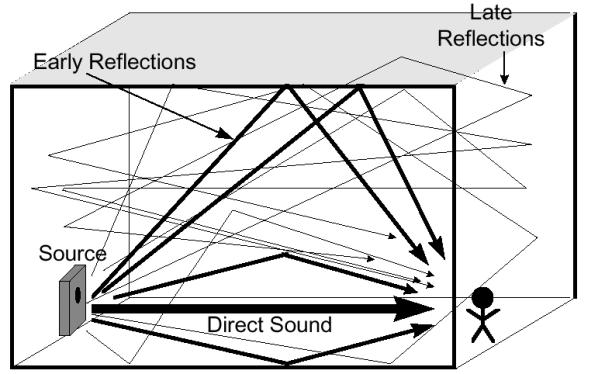
Figur 63, Prinsipp tegning, hentet fra 21065L Audio examples
På grunn av spredningsgraden til de forskjellig frekvensene vil høye og lave frekvenser reflekteres forskjellig. En romklang algoritme baserer deg derfor på en rekke filtre i parallell.
Følgende implementasjon er basert på James A. Moorer’s Reverb algoritme, som også foreslår forsinkelse tider på de forskjelllige blokkene.
[Se 21065L Audio Tutorial s.78]
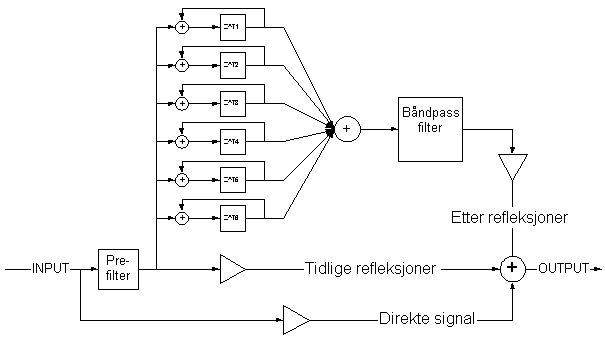
Figur XX, Moorer’s Reverb algoritme
Minne arkitektur
For å kunne lage en effektiv og fungerende algoritme er det viktig å forstå hvordan prosessoren bruker minnet. Som nevnt tidligere har 21065L prosessoren 544kbit internt minne. Dett er organisert inn i to blokker, intern blokk1 og intern blokk2. I tillegg sitter det 2Mx32bit minne på hvert kort. Som nevnt tidligere baserer prosessoren seg på Harvard prinsippet med separate program og data busser. Siden den har separate busser brukes også separate minneområder. For at programkoden skal kunne utnyttet Harvard teknologien makismalt må de forskjellige program delene legges i riktig minne segment.
Programkode og program data bør ligge i det interne minnet, mens tabeller og andre dataelementer kan ligge i den eksterne SDRAM.
Det er viktig å merke seg at DMA bufferne for perifere enheter må ligge i internminnet.
I VisualDSP finnes det derfor en egen filtype som tar seg av minne arkitekturen. Slike filer kalles Linker Description Files, eller .LDF.
Her defineres forskjellige minneområder, slik at Program og Dataminnet blir definert som det skal.
Et problem er at maks størrelse på den interne Program minne blokken er 3824 lokasjoner(48bit) og for Dataminnet , 4096 32bits lokasjoner.
Det vil si at programmets instruksjoner ikke kan ta mer plass enn 3824 instruksjoner. Dette er en klar flaskehalse nå det sitter 2MB på EZ-LAB kortet som ikke kan benyttes.
Det finnes riktignok en metode rundt dette problemet. Ved å bruke DMA på en lur måte i tillegg til å gi Linkeren i VisualDSP spesielle kommandoer lar det seg gjøre å kopiere inn de segmentene av programmet som kjøres der og da fra ekstern SDRAM. Det viste seg at dette var veldig avansert og førte derfor til at vi ikke har implementert dette i vårt program.
Direct
Memory Access, DMA
For at DSP kjernen skal kunne arbeide uavbrutt med valgte vi å benytte oss av DMA kontrolleren som er innebygd som en del av I/O arkitekturen i ADSP21065L prosessoren.
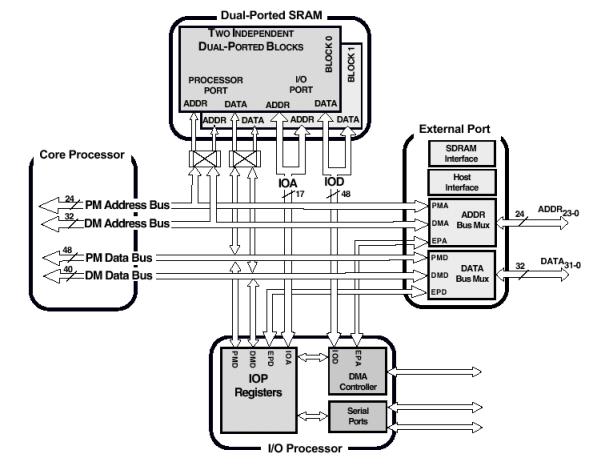
Figur 64, Blokkskjematisk oversikt av ADSP21065L. Hentet fra ADSP21065L User’s Manual
Når mikrokontrolleren sender kontrolldata over den eksterne parallell databussen til DSP prosessoren må det settes opp en kommunikasjonskanal mellom disse. På DSP-siden er det DMA kontrolleren som tar seg av denne oppgaven. Når mikrokontrolleren skriver data er det DMA kontrolleren som latcher dataene inn i et lite buffer. Når dette bufferet er fullt flytter så DMA kontrolleren dataene til en på forhånd definert adresse i det interne minnet i signalprosessoren. Når alle dataene er overført generer DMA kontrolleren et interrupt. DSP kjerne kan deretter bruke dataene i signalalgoritmen.
For at DMA systemet skal fungere må DMA kontrolleren settes opp for å ta i mot informasjon. Dette gjøres ved å skrive til DMA kontroll registrene.
Adressen til DMA kontrolleren skriver til i internminnet må på forhånd defineres i IIEP0 (Internal Index for External Port 0) registert.
I tillegg må det defineres hvor mange ord som skal overføres i CEP0 (Count for External Port 0) og hvor mye adressen skal forandres for hver gang i IMEP0 (Internal Modifierer for External Port 0).
For å aktivere DMA kontrolleren må den settes opp i DMAC0 (DMA Control register ch0).
I dette registeret kan det velges forskjellige parametere for selve overføringen.
Siden mikrokontrolleren vi bruker bare har 16bits bussbredde kan dette konfigureres ved å velge 16/32 Packing Mode i dette registeret.
Ved å sette DMA Enable bittet i dette registeret aktiveres DMA kontrolleren.
For detaljert informasjon se i ADSP21065 User’s Manual kap.9 6 DMA
Serial Ports, SPORT
Det er ofte ikke behov for parallell overføring av data. Kommunikasjonen mellom de to DSP prosessorene og mellom DSP og Codec er eksempler på steder som seriell overføring kan benyttes. Serieportene på ADSP21065L prosessoren kan styres av DMA kontrolleren. Dette er ideelt for vår algoritme siden det hele tiden skal sendes informasjon mellom EZ-LAB kortene og fra DSP til Codec.
Det er to tilgjenglige serieporter på ADSP21065L prosessoren.Vi bruker en til kommunikasjon med AD1819 stereo Codec (SPORT1) og en til kommunikasjon mellom de to EZ-LAB kortene (SPORT0).
En serieport settes opp på samme måte som den eksterne porten som brukes opp mot mikrokontrolleren. Det må defineres en start adresse i det interne minnet i IIR01 eller IIT0A
(Internal Index Receive/Transmit SPORT 0 chA) registeret. Hvilket register som benyttes er avhengig av om det skal sendes eller taes imot data.
Det må også defineres hvor mange ord som skal overføreres og hvor mye adressen skal forandres for hver gang.
Serieportene har også sitt egent kontrollregister hvor overførings detaljer kan velges.
DMA kontrolleren aktiveres for den respektive serieporten ved å sette SDEN (Serial Port DMA Enable) bittet i S[R/T]CTL0A registeret.
For detaljert informasjon se i ADSP21065L User’s Manual kap.9 Serial Ports.
Stemme arkitektur
Den komplette stemmealgoritmen i en musikk synthesizer er en relativt komplisert stykke programvare. Den inneholder avansert signalbehandling og alt må skje i sanntid. I tillegg til dette er det flere oppgaver som må gjøres samtidig og selve system- arkitekturen består ofte av flere prosessorer som skal kommunisere med hverandre.
Først og fremst må stemmealgoritmen kunne spille av lydalgoritmen i sanntid og helst med flere stemmer. En stemme fungerer på samme måte som en tråd i objektorienterte programmerings språk. For hver tangent som trykkes ned skal det lages en ny kopi av den lydgenererende programkoden, som er selvstendig og isolert fra eventuelle andre stemmer. Denne skal så være aktiv og kjøre i sanntid helt til den respektive tangenten slippes opp. Hvis det benyttes omhylningskurver med ”Release” parameteret aktiv skal stemmen henge igjen helt til omhylningskurven dør helt ut. Hvis separate MIDI kanaler benyttes skal algoritmen også kunne spille stemmer i bakgrunnen slik at selv om de fysiske kontrollknappen berøres er det ikke sikkert at de skal ha innvirkning på alle de aktive stemmene.
Dette kan løses på følgende måte.
Alle parametrene som er tilgjenglig fra kontrollflaten må være tabeller like store som antall separate MIDI kanaler som systemet skal kunne behandle. På denne måten kan det differsieres mellom de forskjellige stemmene og de fysiske kontroll parametrene.
Siden hver stemme krever prosessorkraft kan ikke DSP systemet ha et ubegrenset antall stemmer aktivt til en hver tid. Det vanlig er at systemet fjerner den eldste aktive stemmen hvis systemet kjører med maksimalt tillatt antall stemmer og en ny tangent trykkes ned.
Det er ønskelig med flest mulig aktive stemmer, derfor er det viktig å hele tiden tenke på besparelser av prosessorkraft under utviklingen av stemmealgoritmen.
Livsforløp til en stemme:
Note
on -> sendes til DSP ->Oppdatering detekteres->velger riktig
frekvens->ny stemme genereres…
Note
off->sendes til DSP->Oppdatering detekteres->riktig stemme merkes for
fjerning->hvis ”release” holdes stemmen til funkjsjonen dør ut->riktig
stemme fjernes
Vi forsøkte først med en statisk stemme allokering hvor hver parameter i lydalgoritmen var en tabell med like mange plasser som det er noter. Når stemmealgoritmen fikk en stemme aktivering, brukte vi note nummeret som indeks ved alle parameter tabellene. Det viste seg imidlertid at dette var en særdeles dårlig løsning på problemet og hadde flere kritiske svakheter.
For det første krevde denne løsningen alt for mye minne, hvis vi skulle følge MIDI spesifikasjonene med 128 note verdier. Hver eneste parameter i lydalgoritmen måtte være en tabell med 128 plasser. Siden vi bruker over 50 forskjellige kontroll parametere vil hver stemme ta over 5kB minne, noe som er uakseptabelt på grunn av 21065L prosessorens minne behandling med tanke på internminne og DMA buffer. [Se minne behandling]
I tillegg til dette fikk vi et problem med Release funksjonen til omhylningskurven. Som nevnt tidligere skal en stemme holdes aktiv etter at tangenten er sluppet opp hvis release parameteret i omhylningskurven er aktiv. Hvis tangenten nå trykkes ned på nytt samtidig som release delen fortsatt er aktiv fra forrige gang, skal det allikevel genereres en ny unik stemme. Dette fungerte ikke i vår statiske struktur, siden hver note hadde sin faste indeks i variabel tabellene. Den nye stemmen ”skrev” derfor over release stemmen.
Vi fant ut at det ville være lurt å organisere hver stemme som en datastruktur, altså et objekt. Ved å da legge disse objektene inn i en blanding av en tabell og en kø, kunne aktiveringen og deaktiveringen enkelt implementeres.
Når en ny stemme genereres legges indeksen stemmen får i stemme køen inn i en ny tabell med note nummeret som indeks. På denne måten kan vi deaktivere riktig stemme når den tid kommer.
Siden alle stemmene deler selve lydalgoritmen er det bare de forskjellige pekerne og tellerne som gjør hver enkelt stemme unik. Stemme strukturen må derfor ha alle disse unike variablene som private variabler. Det må lages generelle metoder for å lage nye stemmer, fjerne stemmer og rydde stemme køen. Stemme systemet kan visualiseres på følgende måte:
Figur 65, Stemmestruktur.
Første noe som legges inn er note 25, deretter 23 og 21. Ende pekeren peker alltid på eldste note. Hvis tabellen er tom peker den på –1 (null).
Når en ny note legges inn inkrementeres ende pekeren og den nye stemmen legges på denne posisjonen. Denne indeksen blir deretter lagt inn i en kø-indeks tabell. Denne tabellen tar note nummeret som indeks. Note-indeks tabellen oppdateres hver gang stemme-køen forandres, som for eksempel ved note deaktivering, slik at den alltid inneholder riktig stemme-indeks på notene.
Hvis note 23 skal slettes, gjør slette funksjonen et oppslag i kø-indeks tabellen for å få riktig indeks til stemme-køen. Slette funksjonen har nå 1, og kan slette plass 1 i stemme køen. Plass 2 flyttes til plass 1, det samme gjør ende-pekeren og kø-indeks tabellen oppdateres.
Figur 66, Stemme system etter sletting.
Timing – Timer
Timing er et meget viktig punkt i et digitalt system. I vårt tilfelle må D/A omformeren hele tiden fores med nye samples med korrekte intervaller. Hvis timingen ikke opprettholdes vil det oppfattes som et frekvens hopp i lydsignalet.
ADSP21065L prosessoren har to innebygde timere. Disse fungerer slik at de dividere den interne prosessorklokken på 60KHz på et heltall. Dette tallet blir deretter dekrementert for hver klokkepuls etter at timeren er aktivert. Når verdien er lik null genereres et interrupt.
Denne tiden settes i TPERIOD[0/1] registert.
AD1819A Codec kretsen generer slev interrupt når den trenger nye samples. Vi benytter timerne til å styre kommunikasjonen mellom EZ-LAB kortene.
Her er flyt diagrammet til hovedprogrammet. Flytskjemaet avviker noe fra den egentlig koden. Blant annet likte ikke kompilatoren norske tegn i koden, derfor finnes det en del engelske navn på variabler og funksjoner.
|
|
|
Figur 67, Hovedprogrammflyt 1
|
|
|
Figur 68, Hovedprogramflyt 2
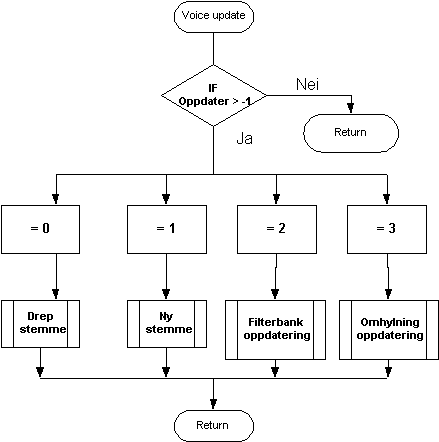
Figur 69, Hovedprogramflyt 3
|
|
|
Figur 69 b, Hovedprogramflyt 4
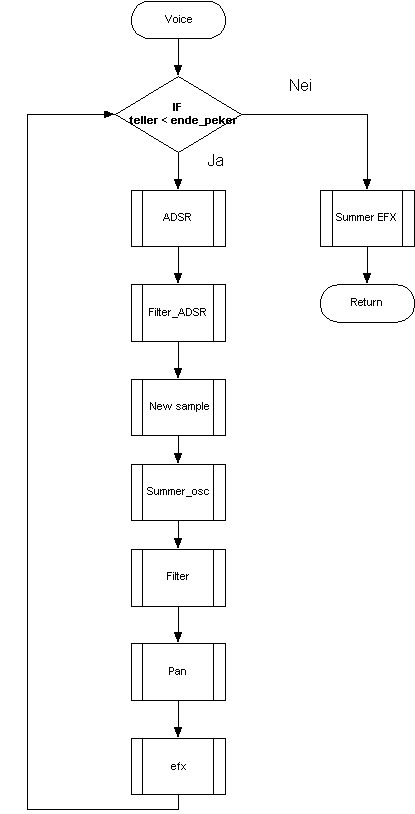
Figur 70, Hovedprogramflyt 5
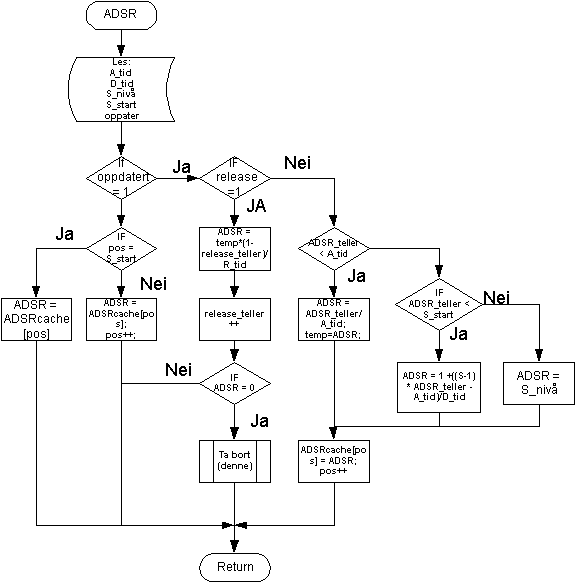
Figur 71
|
|
|
Figur 72
DSP2
|
|
|
Figur 73
|
|
|
Figur 74
Figur 75
|
|
|
Figur 76
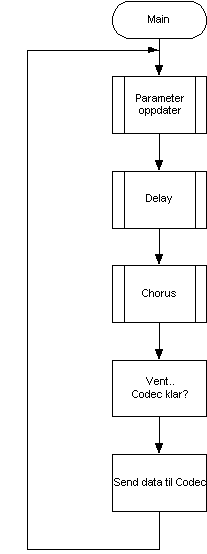
Figur 77
Mikrokontroller – Software og hardware implementasjon
Sammenkoblingskort
Sammenkoblingskortet er ferdig tegnet i Traxedit og lagt ut. Kortet er boret for montering av komponenter. Det er ikke ferdig montert og derav ikke testet. Kortet er inspisert i lupe og utbedringer av defekte baner er gjort. Bilde av kretskortet med komponenter finnes i papirvedlegget under ”Bilder/Sammenkoblingskort”. Kretskortutlegget finnes som PDF fil i det elektroniske vedlegget under ”Kretskortutlegg”.
Software
Hovedprogrammet, main()
Hovedprogrammet er implementert i henhold til softwareprinsippene i kapittelet om ”Mikrokontroller software prinsipper”. I tillegg har vi definert variable og minneområder for periferkomponentene i henhold til tabellen ”Minne konfigurasjon av periferenheter på sammenkoblingskort, med angitte minneområder for ARM mikrokontroller”. Tabellen finnes i papirvedlegget. Programmet er ikke ferdig utviklet og testet ut over syntaktisk feilsjekking.
MIDI-algoritme, midi()
MIDI-algoritmen er implementert i henhold til spesifikasjon i softwareprinsippene.
Algoritmen er kjørt på prosessoren med keyboard input, og virker tilfredsstillende. Full test av algoritmen kan først foretas når sammenkoblingskort er ferdig.
Atmel EB01 M40400 utviklingskit
En av hovedbestanddelene i systemet er Atmel mikrokontrolleren. I vår laboppstilling er denne plassert på et utviklingskort levert av Atmel. Alt minne til mikrokontrolleren er også plassert på utviklingskortet. Hvordan dette er konfigurert redegjøres for i minnearkitektur delen. Utviklingskortet har flere brytere og dioder, men disse er ikke av interesse for vårt system. Det kjøres en ferdig definert software på kortet for å gjøre det mulig å kjøre en debuggermonitor over serieporten til en vanlig PC. Det er ferdig oppkoblede RS232 omformere på Atmelkortet for standard RS232 kommunikasjon med PC debuggingssoftware.
Utviklings –software og -hardware
Til utvikling av software til Atmelprosessoren har vi brukt en Compaq Armada 6500 PC med MS Windows 98 SE og MS Windows NT 4.0 SP6. Til softwareutvikling har vi brukt ”ARM Software Developer Studio 2.5” og ”Greenhill's Multi Development Kit for Atmel ARM7TDMI AT91”
Følgende software har vært i bruk under prosjektet til forskjellig formål:
Word 2000 – Tekstbehandling.
Excel 2000 – Kalkulasjoner.
Explorer 5.2 – Webskummleser.
Outlook - E-post klient
Visio 5.0 – Figurtegning og modellutvikling.
Macromedia
Dreamweaver - HTML editor.
Mathematica 4.0 – Beregninger og simuleringer.
Matlab 5.3 med Simulink, Signal Processing Toolbox og Control System Toolbox – simulering og databehandling.
Protel Traxedit og Traxplot MS DOS - Kretskortutlegg
Leap FTP klient – FTP filoverføring.
Sambar - FTP server software
Adobe Acrobat Reader og Acrobat Destiller – Word dokument til PDF konvertering.
SpektraPlus – FFT-analyseprogram.
Winrar – komprimerings og dekomprimerings -program
Paint Shop
Pro og Photoshop 5.5 – Bildebehandling.
Sound Engine - funksjonalitet
Rent funksjonelt fungerer hele lydalgoritmen som den skal. Stemmer kan legges til og fjernes og eventuelle stemme overbelastninger blir tatt hånd om.
Det første man legger merke til når hele lydalgoritmen kjøres er at det ikke genereres ordentlig lyd. Ved å bruke en teller på DSP1 Main() løkken fant vi ut at bare 70% av programløkken ble eksekvert på 1/48000 sekund.
Serie kommunikasjonen mellom EZ-LAB kortene er i beste fall ustabil. Dette kan komme av at vi ikke hadde en ordentlig kabel og brukte det som er kjent som ”spreng-tråd” istedenfor. Dette er neppe noe egnet medium for å sende 20MHz pulstog.
Del blokkene
Oscillator delen
Sagtannbølgeform
Testsignalet er 500Hz sagtann.
Som vi ser på tidsplan figuren får sagtann bølgen små ”ører” akkurat i svitsje punktet. Dette kommer sannsynligvis av at signalet blir lettere filtrert et eller annet sted i testutstyret.
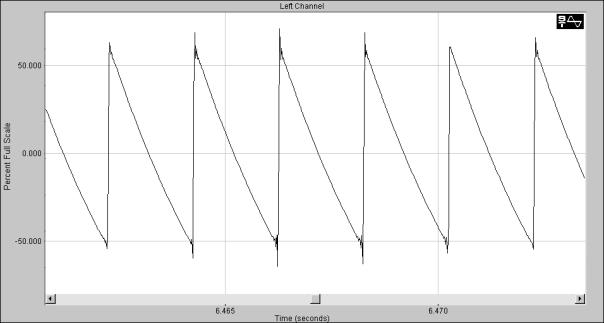
Figur 78, Sagtann - Tidsplanet
Testsignalet er 500Hz sagtann.
Som vi ser på tidsplan figuren får sagtann bølgen små ”ører” akkurat i svitsje punktet. Dette kommer sannsynligvis av at signalet blir lettere filtrert et eller annet sted i testutstyret.
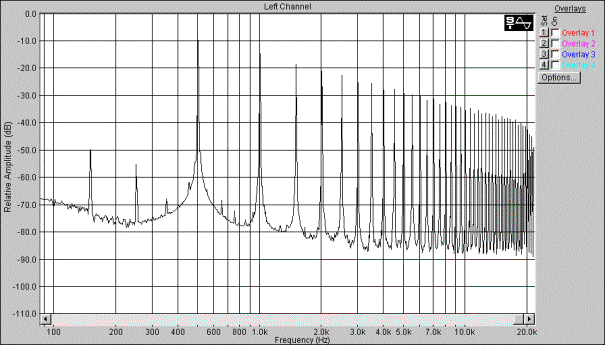
Figur 79, Sagtann - Frekvensplanet
Hvis vi ser på frekvensplan plottet ser vi at det er en tydelig topp ved grunnfrekvensen 500Hz. Vi ser at det er en ny resonans for hver harmonisk over dette, altså ved 1000, 1500, 2000, 2500Hz o.s.v som stemmer meget bra med teorien.
Firkantbølgeform
Figur 80, Firkantbølgeform i frekvensplanet.
Plottet av firkantbølge samplingen viser at mye av energien i signalet er samlet om 500Hz eller grunnfrekvensen, det er en markant forskjell på hvor bredt energien i signalet er sammenlignet med sagtannbølgeformen. Det er interessant å se hvordan overtonene forplanter seg oppover i frekvensplanet, da man tydelig kan se at annen hver harmoniske komponent har høyt energiinnhold. Plottet er som forventet m.h.p. at de harmoniske tonene kommer på 500Hz + x*500 hvor x er et heltall.
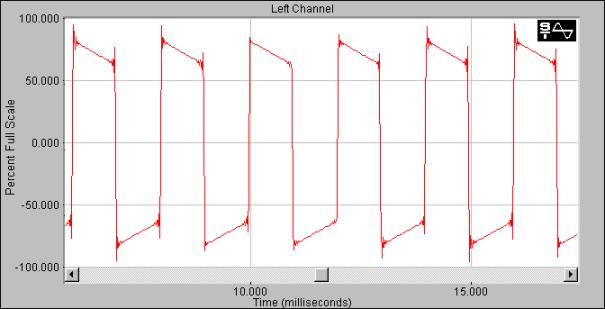
Figur 81, Firkantbølgeform i tidsplanet.
Av plottet til den samplede firkantbølgeformen ser vi at toppen av firkanten er sterkt modellert. Ved sammenligning med avlesning av oscilloscopsweep ser vi en markant forskjell i gjengivelse av bølgeformen. Scopbildet viser langt steilere flanker og en jevn amplitude på høy puls. Filter i samplingsutstyret gir antakelig en feilaktig gjengivelse av amplitudeforholdet i en tidsserie.
LFO
Testsignalet er 400Hz sagtann.
Denne funksjonen fungerer. Siden det er litt problematisk å kun teste denne funksjonen uten å blande inn andre funksjoner valgte vi å spille den av. I og med at denne funksjonen ikke er beregnet for audio frekvenser vil den vise tydelig kvantiserings støy siden den blir generert med en samplings frekvens på 10kHz.
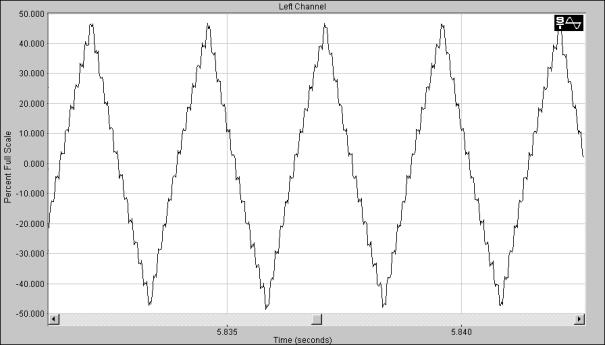
Figur 82, LFO Tidsplanet
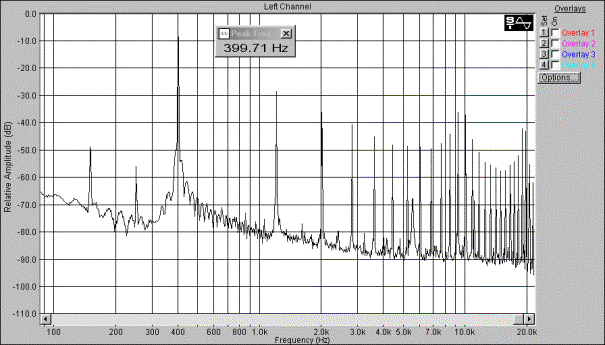
Figur 83, LFO - Frekvensplanet
Grafen har en tydelig topp ved grunnfrekvensen 400Hz og de harmoniske.
FM
Figuren viser firkantbølgen modulert med sagtann på 1Hz. Frekvensen begynner høyt og faller 4oktaver. Dette ser vi kan stemme med tidsplan figuren. Lyden som skapes kalles for ”Chirp” på engelsk og høres ut dom et slags smell. Denne lyden er repetitiv. Det er derfor frekvensen plutselig gjør et kjempesprang i det sagtann bølgen svitsjer fra 1 til –1.
Hvis vi ser på frekvensplan figuren ser vi at frekvensresponsen faller rettlinjet. Siden frekvensaksen er logaritmisk stemmer dette siden modulasjonsindeksen går i oktaver.
Figur
84, FM Chrip tidsplanet
Ringmodulasjon
Figuren viser et sinus signal på 768Hz ringmodulert med et annet sinus signal på 228Hz.
Vi vet fra før at denne funksjonen skal gi et sum signal og et differanse signal.
768-228 = 540 og 768+228 = 996. Vi ser at toppene i frekvens figuren stemmer bra med teorien. Den ene er på ca. 550Hz og den andre på ca. 1000Hz.
Vi ser av tidsplan figuren at signalet fortsatt er periodisk, men har blitt litt mer komplisert enn hva det var før modulasjon (kun to sinus signaler).
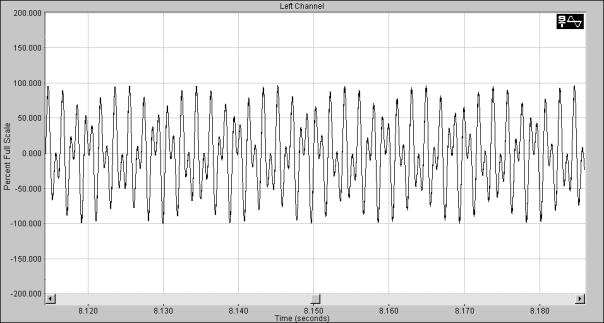
Figur 86, Ringmodulasjon i tidsplanet
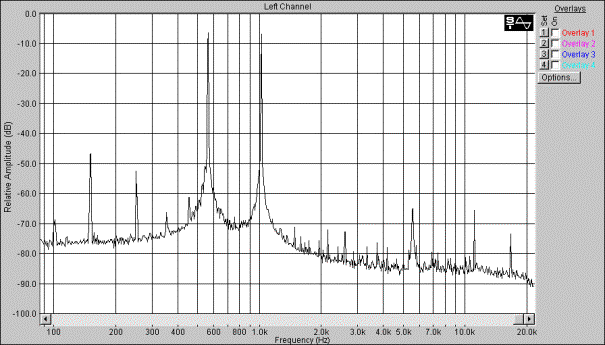
Fig 87 Ring modulasjon i frekvensplanet.
Omhylnings kurver
Siden omhylnings kurver er et kontrollsignal var den eneste måten å vise denne funksjonen å sende støy gjennom en ADSR styrt forsterker. Vi ser tydelig at det konstante støy signalet har tatt formen til omhylningskurven.
Fig. 88 ADSR omhylningskurve i tidsplanet.
Støy
Støy signalet skal egentlig være helt tilfeldig uten synlig harmonisk innhold. I frekvensplanet skal responsen være lik for alle frekvenser. Vi må huske at rand() funksjonen sannsynligvis ikke er helt tilfeldig som vil føre til at signalet ikke oppfører seg helt slik vi forventer av hvit støy. Den konklusjonen vi kan trekke av disse figurene er at signalet IKKE er hvit støy, men en farget variant.
Fig 89 Støy i tidsplanet
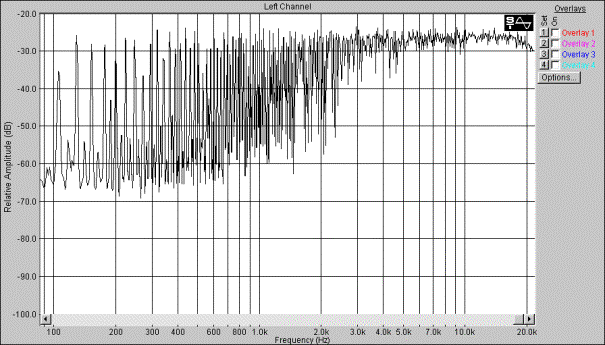
Fig. Støy i frekvensplanet
Filteret
For å bedømme et filter må filterets frekvensrespons analyseres.
For å gjøre dette kreves relativt avansert og nøyaktig måle utstyr, som vi dessverre ikke har vært i besittelse av. Framgangsmåten vi benyttet oss av for å forsøke å måle filterresponsen var først å sendes støy igjennom filteret, og deretter sveipe et sinus signal.
For at støy metoden skal gi et riktig resultat må det benyttes hvit støy. Vi har allerede konstatert at vi ikke har ekte hvit støy. Disse måle resultatene er derfor ikke helt til å stole på.
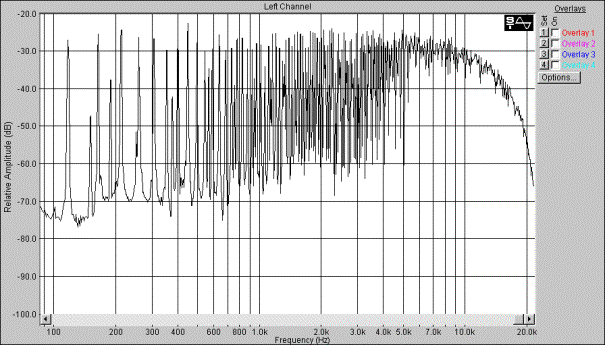
Fig.90, Filtrert støy i frekvensplanet.
Filteret vi har benyttet oss av i akkurat denne testen er et 2.orden lavpass filter med knekkfrekvens på rundt 1000Hz. Vi ser av grafen at frekvensresponsen avtar for høye frekvenser. Riktignok ikke merkbart før ved omtrent 10kHz,et resultat som ikke stemmer spesielt bra med hva vi på forhånd hadde forventet.
Ved å bruke frekvens sveip metode fikk vi disse resultatene:
Fig. 91, 2.ordens lavpass filter i tidsplanet.
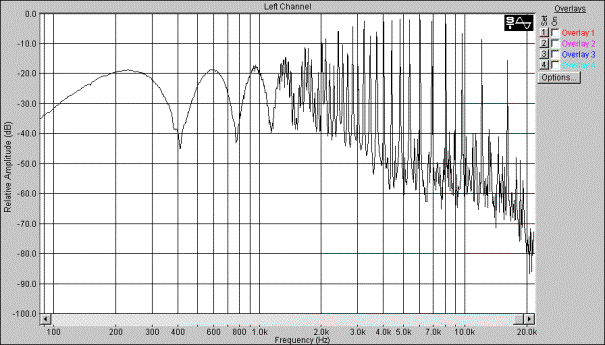
Fig. 92 2.ordens filter respons i frekvensplanet.
Det første vi legger merke til ved tidsplangrafen er at den hakker veldig for høye frekvenser. Det var meningen at sinus sveipte vi genererte skulle øke jevnt i frekvens. Det gjør det åpnbart ikke. Denne testen har avslørt en alvorlig feil i lydalgoritmen, siden det tydeligvis kun er noen frekvenser som kan gjengis korrekt.
Frekvens sveip metoden er av denne grunnen heller ikke til å stole på siden vi nå har påvist feil i referanse signalet.
Siden vi ikke har flere måter å teste filteralgoritmen på har vi valgt å fortsette med frekvens sveip metoden siden vi allikevel kan si generelle ting om responsen.
Selv om frekvens sveipet hopper i frekvens er amplituden konstant. Hvis vi ser på tidsplan grafen ser vi at frekvens responsen avtar tydelig med økende frekvens. Det ser derfor ut som filteralgoritmen fungerer. Hvis vi studerer responsen i frekvensplanet er egentlig det enste vi kan trekke ut at vi ser hvilke frekvenser sveipet hopper i mellom. Vi ser derfor heretter kun på figurer i tidsplanet.
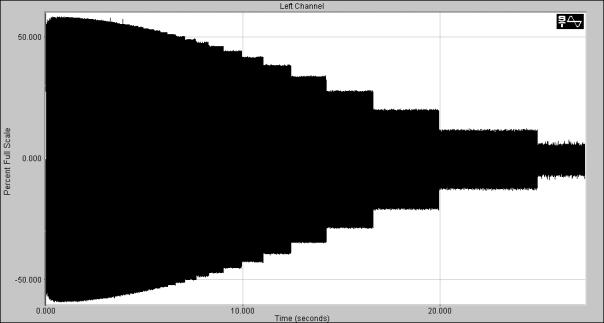
Fig. 93 4.ordens filter i tidsplanet
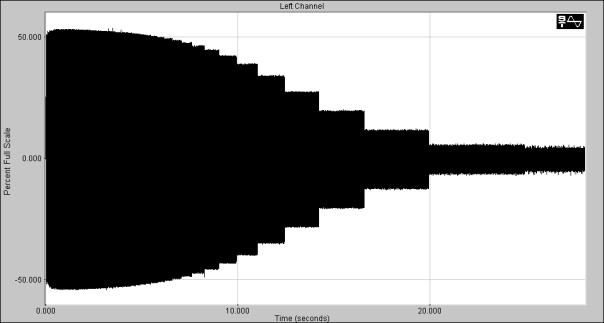
Fig 94 6.ordens filter i tidsplanet
Ser vi nøye på disse to figurene ser vi at dempningen øker med høyere ordens filtre. Vi hadde forventet oss en noe større forskjell på de forskjellige ordenene siden et 4.ordens filter skal ha 24dB dempning pr. oktav, og et 6.ordens filter 36dB pr. oktav.
Figuren under viser også et 6.ordens filter. Denne gangen er resonansparameteren justert opp til en verdi som tilsvarer 0.23 i radius ved pol plasseringen. Vi ser at det er en markant økning i amplituden umiddelbart før knekkfrekvensen, akkurat som forventet.
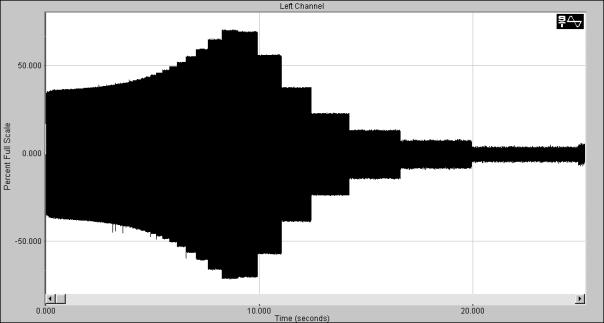
Fig 95 6.ordens filter med resonans
Vi har en rekke punkter for videre utvikling av systemet og ferdigstilling av påbegynte hardware og software oppgaver. Det mest åpenbare er å montere alle kretskortene ferdig, og teste disse. Videre ønsker vi å implementere og utvikle software for mikrokontrolleren slik at systemet fremstår som en funksjonell prototype.
Det kan komme på tale å lage et komplett kretskort med mikrokontroll og flere DSP prosessorer. Det er aktuelt å vurdere andre DSP prosessorer til dette formålet, da ytelsen på ADI SHARC 21065L er i underkant av den prosessorkraften vi trenger for å implementere alle algoritmene vi ønsker. En alternativ videreutviklet modell er skissert i figuren under.
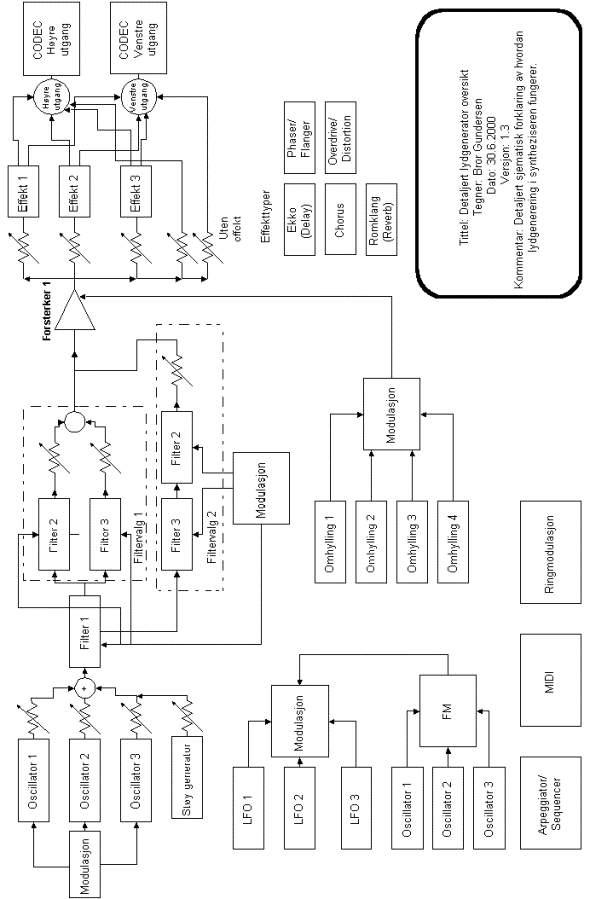
Svakheter og forbedringer
Som vi allerede har vært inne på finnes det flere klare svakheter med denne implementasjonen.
- Program strukturen har en klar svakhet i at den ikke kan spille av en enste hel stemme slik som funksjonene er implementert for øyeblikket.
- Frekvens styringen har en klar svakhet i at den ikke kan generere alle frekvensene i det hørbare området. Årsaken til steppingen ligger i hvordan bølgeformenes periode regnes ut. Vi benytter formelen: periode = punktprøvningsfrekvens / ønsket frekvens. Siden variabelen periode er en INT rundes perioden av til nærmeste hele tall. Jo høyere frekvensen er, jo mer signifikant blir denne avrundingsfeilen.
- De fleste funksjonene er ikke korrekt parameterisert. Dette betyr at noen funksjoner skulle hatt en høyere oppløsning for bestemte intervaller. Dette gjelder blant annet filterets resonans og frekvens kontroll.
- Vi merket oss under filter testingen at det hendte titt og ofte at frekvensen gjorde små variasjoner når den egentlig skulle være helt konstant. Vi har ikke funnet den eksakte årsaken til dette fenomenet, men mistankene går i retning av synkroniseringsproblemer med codec kretsen. Hvis sample strømmen spilles av fortere, øker frekvensen. Hvis lydstrømmen spilles av saktere minker den. Dette området krever større testing.
- Anskaffe bedre testutstyr slik at det er kun implementasjon som måles og ikke alt annet.
Hva kan så gjøres for å utbedre disse svakhetene?
For å øke antall aktive stemmer må det gjøres noe med hvordan programmet eksekveres. Enten må eksekveringen utføres raskere, eller så må det bli færre operasjoner å utføre. En annen mulighet er å senke punktprøvingsfrekvensen i selve lyd algoritmen slik at det går lengre tid mellom hver punktprøve. Et annet alternativ kan være å skrive hele koden om i assembler, for på denne måten omgå eventuelle svakheter i kompilerings prosessen. En ikke fullt så drastisk fremgangsmåte kan være å skaffe et analyseverktøy som kan forbedre den eksisterende C koden.
Problemet med periode tiden har vi ingen umiddelbar løsning på. Sannsynligvis må vi finne en annen måte å løse oscillator genereringen. De andre nevnte problemene må nok løses ved hjelp av videre undersøkelser og prøver.
Denne oppgaven hadde som mål å belyse de forskjellige aspektene ved en digital audio syntheeizer for tilslutt å utvikle en fungerende prototyp
Vi føler at vi sitter igjen med en dyp innsikt i digitale audiosystemer for både program og maskinvare. Vi har implementert de forskjellige del blokkene som ofte brukes ved subtraktiv syntese på en digital signalprosessor.
Vi har fått en meget god forståelse av hvordan mikroprosessor systemer fungerer, vi har sett på både program og maskinvare og hvordan data kan hentes inn fra analoge komponenter og benyttes av digitale mikroprosessorer. Vi studerte også grundig digitale kretskort metoder og designet vårt eget system for datainnhenting sammen med EB01 plattformen. Dette resulterte i en avansert kretskortløsning for avlesning av 48 analoge potensiometer og sammen kopling av tre uavhengige mikroprosessor systemer.
Vi har i tillegg til dette fått en kjennskap med programmeringsspråket C og hvordan datastrukturer kan brukes for å organisere parallelle sanntids stemmestrukturer.
Det viste seg etter hvert at denne oppgaven tok for seg meget stort fagområde. Dette førte til at noen av de målene vi hadde satt med denne oppgave ikke kunne implementeres på den tidsfristen som er satt for en slik hovedoppgaven ved Ingeniørutdanningen.
Dette gjelder selve prototype modellen. Alle de fysiske delene har blitt konstruert og all programvaren har blitt drøftet og strukturert med flytskjema.
Det som gjenstår er selve den praktiske oppkoplingen og sammensetningen av de forskjellige utviklingskortene og egenproduserte kretskort.
Når det gjelder programvare implementeringen ble noe mer avansert enn vi hadde tenkte på forhånd. Vi la til en del funksjoner og muligheter underveis for å få et mer komplett og fullstendig sluttprodukt. Samtidig viste det seg at noen funksjoner var relativt kompliserte og tidkrevende å implementere. Dette gjelder spesielt Romklang funksjonen som ikke har blitt implementert med C-kode.
Andre programvare funksjoner som ikke har blitt implementert i C kode er de funksjonene som er knyttet direkte opp mot uferdige maskinvare løsninger. Dette gjelder særlig MIDI protokollen. Siden selve MIDI kretsen ikke er implementert ble det vanskelig å lage en konsistent C kode løsning.
Det finnes en rekke fremtidige forbedringer og utvidelser av systemet. Den mest åpenbare er å ferdigstille kretskortet og å teste dette. Det finnes også mye å ta tak i ved de forskjellige programvare implementasjonene siden raskere kode gir mulighet for utvidelse av systemet med tanke på antall stemmer og antall funksjoner i selve lyd algoritmen. Eventuelt kan også andre syntese teknikker utforskes videre.
Dette prosjektet har vært en meget lærerik prosess og vi føler at vi nå sitter inne med kunnskap langt over hva vi hadde regnet med da vi startet med denne oppgaven. Vi føler oss derfor vel rustet til videre studier og arbeide innfor disse områdene, og spesielt digital audio.
Oslo 05.07.2000
Nils Petter Lyngstad Bror Gundersen
Innholdsfortegnelse vedlegg:
Tabeller
Knappefunksjoner. s. 103
Minne konfigurasjon av periferenheter på sammenkoblingskort,
med angitte minneområder for ARM mikrokontroller s. 103
Konfigurasjon av knappeinnganger på bussdrivere og skjematisk bussdiagram
med angitte knappeinnganger. s. 104
Bilder
Kretskort for venstre side av kontrollflate med monterte potensiometere. s. 106
Kretskort for høyre side av kontrollflate med monterte potensiometere. s. 107
Kretskort for senter av kontrollflate med monterte potensiometere. s. 108
Kabinett for montering av potmetere, knapper og display. s. 108
Sammenkoblingskort. s. 109
ADSP 21065L EZ-LAB – DSP utviklingskort. s. 110
Atmel AT 91 M40400 - Utviklingskort. s. 111
Display og inverter fra displayets fremside. s. 112
Displayets bakside og inverter. s. 113
SHARC-kode
DSP1 s.
115
DSP2 S.134
Atmel-kode
Hovedprogram, main() s. XX
MIDI algoritme, midi() s. XX
Elektronisk vedlegg
Finnes på vedlagt CD. Linkene under virker ikke ennå –
blir oppdatert i løpet av august 2000.
Dokumentasjon for Sharc 21065L DSP prosessor, EZ
kit utviklingskit og ADI 1819 Codec
Analog Devices DSP 21065L SHARC
User's Manual
Analog Devices DSP 21065L SHARC
Technical Reference
Visual DSP User's guide and
Reference
ADI 1819 Codec interfaced to 21065L
Dokumentasjon for Atmel mikrokontroller og mikrokontroller kit
Atmel 91 M40400 Electrical and
Mechanical Caracteristics
Mikrokontroller periferkomponenter
74HC154 - 4 til 16 adressedekoder - datablad
74HC374 - D-flip flop- datablad
74HC244 - Linjedriver- datablad
6N139 - Optokobler- datablad
Analog Devices AD7859 - Analog til digital omformer- datablad
ADC klokkekretskomponenter:
74HC14 - Schmittrigger- datablad
74HCU Familie komponenter- datablad
74HCU04- Ubuftret inverter- datablad
Display
Display
Controller
Inverter
Spesifikasjon av inverter er beskrevet i G242 Users Manual
MIDI dokumentasjon
Hinton Instruments' Guide to Professional MIDI
Eksempellyder
Lydene er i *.wav format
Oscillatorer
Modulasjon
LFO
Filter
Filtersveip 2. ordens lavpassfilter
Filtersveip 4. ordens lavpassfilter
Filtersveip 6. ordens lavpassfilter
Kretskortutlegg
|
|
Manualer til andre virtuelle analoge synther
Tabeller
Minne konfigurasjon av periferenheter på sammenkoblingskort, med angitte minneområder for ARM mikrokontroller
|
Enhet |
4 bit adresse på adressedekoder |
Minneområde i binærformat angitt i 24 bit for ekstern bus |
Minneområde i hexadesimaler 32 bit |
Databus-bredde |
|
AD omformer 1 |
0111 |
0111 0000 0000 0000 0000 0000 |
0xFF 70
00 00 |
16 bit |
|
AD
omformer 2 |
0110 |
0110 0000 0000 0000 0000 0000 |
0xFF 60
00 00 |
16 bit |
|
AD
omformer 3 |
0101 |
0101 0000 0000 0000 0000 0000 |
0xFF 50
00 00 |
16 bit |
|
AD
omformer 4 |
0100 |
0100 0000 0000 0000 0000 0000 |
0xFF 40
00 00 |
16 bit |
|
AD
omformer 5 |
0011 |
0011 0000 0000 0000 0000 0000 |
0xFF 30
00 00 |
16 bit |
|
AD
omformer 6 |
0010 |
0010 0000 0000 0000 0000 0000 |
0xFF 20
00 00 |
16 bit |
|
Knappe
busdriver 1 + 2 |
1100 |
1100 0000 0000 0000 0000 0000 |
0xFF C0
00 00 |
16 bit |
|
Knappe
busdriver 3 |
1101 |
1101 0000 0000 0000 0000 0000 |
0xFF D0
00 00 |
8bit |
|
Display |
0001 |
0001 0000 0000 0000 0000 0000 |
0xFF 10
00 00 |
8 bit |
|
ARM til
DSP latch |
1110 |
1110 0000 0000 0000 0000 0000 |
0xFF E0
00 00 |
16 bit |
|
DSP til ARM latch |
1111 |
1111 0000 0000 0000 0000 0000 |
0xFF F0
00 00 |
16 bit |
Konfigurasjon av knappeinnganger på busdrivere og skjematisk busdiagram med angitte knappeinnganger.
Merking i forhold til dokumentasjon av 74HC244 linjedriver.
|
Knappeinngang |
Driver 1 |
Driver 2 |
Driver 3 |
|
|
|
|
|
|
1 |
1A1 |
|
|
|
2 |
1A2 |
|
|
|
3 |
1A3 |
|
|
|
4 |
1A4 |
|
|
|
5 |
2A4 |
|
|
|
6 |
2A3 |
|
|
|
7 |
2A2 |
|
|
|
8 |
2A1 |
|
|
|
9 |
|
1A1 |
|
|
10 |
|
1A2 |
|
|
11 |
|
1A3 |
|
|
12 |
|
1A4 |
|
|
13 |
|
2A4 |
|
|
14 |
|
2A3 |
|
|
15 |
|
2A2 |
|
|
16 |
|
2A1 |
|
|
17 |
|
|
2A4 |
|
18 |
|
|
2A3 |
|
19 |
|
|
2A2 |
|
20 |
|
|
2A1 |
|
21 |
|
|
1A1 |
|
22 |
|
|
1A2 |
|
23 |
|
|
1A3 |
|
24 |
|
|
1A4 |
Databus konfigurasjon med plassering av knappeinnganger for knappene 1-16 på linjedriver 1 og 2:
|
Bit nr |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Knappe inngang |
16 |
10 |
11 |
12 |
9 |
15 |
14 |
13 |
8 |
7 |
2 |
3 |
4 |
1 |
6 |
5 |
Databus konfigurasjon med plassering av knappeinnganger for knappene 17-24 på linjedriver 3.
Merknad: her brukes 8 bit busbredde med de 8 mest signifikante bitene i bruk.
|
Bit nr |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Knappe inngang |
20 |
22 |
23 |
24 |
21 |
19 |
18 |
17 |
X |
X |
X |
X |
X |
X |
X |
X |
Knappefunksjoner
|
Knappe nummer – korresponderende
knappeinngang på sammenkoblingskort |
Knappefunksjon |
|
1 |
Lagring |
|
2 |
Part 1 valg |
|
3 |
Part 2 valg |
|
4 |
Part 3 valg |
|
5 |
Part 4 valg |
|
6 |
Midikanal opp |
|
7 |
Midikanal ned |
|
8 |
Ikke bestemt |
|
9 |
Ikke bestemt |
|
10 |
Ikke bestemt |
|
11 |
Ikke bestemt |
|
12 |
Ikke bestemt |
|
13 |
Ikke bestemt |
|
14 |
Ikke bestemt |
|
15 |
Ikke bestemt |
|
16 |
Ikke bestemt |
|
17 |
Ikke bestemt |
|
18 |
Ikke bestemt |
|
19 |
Ikke bestemt |
|
20 |
Ikke bestemt |
|
21 |
Ikke bestemt |
|
22 |
Ikke bestemt |
|
23 |
Ikke bestemt |
|
24 |
Ikke bestemt |
Bilder
Utlagte
kretskort
Kretskort for venstre side av kontrollflate med monterte potensiometere.
Kretskort for høyre side av kontrollflate med monterte potensiometere.
Kretskort for senter av kontrollflate med monterte potensiometere.
Kabinett for montering av potmetere, knapper og display.
Sammenkoblingskort. Se rapporten s. XX for beskrivelse av kortet.
Utviklingsverktøy
ADSP 21065L EZ-LAB – DSP utviklingskort.
Atmel AT 91 M40400 - Utviklingskort.
Display
Display og inverter fra displayets fremside.
Displayets bakside og inverter.
DSP Program kode
DSP1
/***************************************************************************
***************** D
S P 1 K O D E
*************************
***************************************************************************
H O V E D P R O S J E K
T HIO V Å R 2 0 0 0
Dette er selve lyd algoritmen. Koden stå å generer samples kun uavbrut
av noen super interrupts() som har minst overhead av alle interruptene.
Koden er ikke 100% ferdig siden ARM-EP_DMA ikke er testet ennå.
Det er derfor noen av DMA bufferene ikke blir initialisert og at mange
av variablene ikke er deklartert som extern volatile.
Siden DSP-DSP kommunikasjonen fungerer dårlig er heller ikke SPORT koden
100% komplett...
På grunn av lange variabelnavn ser desverre noe av denne koden litt rotete ut.
Jeg har valgt å ikke bryte linjene på denne måten vet jeg at koden virker som
den skal.
----------------------------------------------------------------------------
INCLUDES
--------------------------------------------------------------------------*/
#include
<def21065l.h>
#include
<21060.h>
#include
<signal.h>
#include
<filters.h>
#include
<math.h>
#include
"1819regs.h"
#include
<stdlib.h>
/*--------------------------------------------------------------------------
KONSTANT & MACRO DEFINISJONER
----------------------------------------------------------------------------
*/
#define MIDI_KANALER 4
#define ANT_STEMMER 10 //heh =)
#define ENV_SIZE 288000 /* (max_A_tid+max_D_tid+max_R_tid)- her: 48kHz*6 */
#define SAMPLE_TID 0x0000004E2 /*2xCLK_in / Sample_frekvens -> 60KMHz/48kHz */
#define
SetIOP(addr, val) (* (int *) addr) =
(val)
#define
GetIOP(addr) (* (int *) addr)
/*--------------------------------------------------------------------------
EKSTRNE DEKLARASJONER
--------------------------------------------------------------------------*/
/*--------------------------------------------------------------------------
GLOBALE DEKLARASJONER
--------------------------------------------------------------------------*/
int
sample_fq = 48000;
int i;
int j;
// FIRKANT
volatile float Firkant_oktav[MIDI_KANALER];
volatile float Firkant_fin[MIDI_KANALER];
float firkant_sample;
float firkant_mod_sample;
float firkant_periode;
int firkant_halv_periode;
volatile int Firkant_mengde[MIDI_KANALER];
extern volatile float Firkant_FM_mengde[MIDI_KANALER];
volatile float Firkant_FM_dybde[2][MIDI_KANALER];
volatile float PWM[MIDI_KANALER];
// SAGTANN
volatile float Sagtann_oktav[MIDI_KANALER];
volatile float Sagtann_fin[MIDI_KANALER];
float
sagtann_sample=0;
float
sagtann_mod_sample;
float
saw_sample=0;
volatile int Sagtann_mengde[MIDI_KANALER];
volatile float Sagtann_FM_mengde[MIDI_KANALER];
volatile float Sagtann_FM_dybde[2][MIDI_KANALER];
int sagtann_periode;
float Trekant[MIDI_KANALER];
int sagtann_halv_periode;
// LFO
int
lfo_sample_fq=10000;
int lfo_halv_periode=0;
volatile int Lfo_frekvens[MIDI_KANALER];
volatile
float lfo;
int oppdater_lfo;
int lfo_oppdatert;
// SAMPLE
float
output_float_sample = 0.0;
float stemme_sample;
float
oscsum_sample;
int fyr;
volatile int Forvrengning[MIDI_KANALER];
int
max_level;
//ADSR. Tids-parameterene er i samples
volatile float ADSR_mengde[MIDI_KANALER];
volatile int A_tid[MIDI_KANALER];
volatile float Gain[MIDI_KANALER]={2,1,1,1};
volatile int D_tid[MIDI_KANALER];
volatile float S[MIDI_KANALER];
volatile int S_start[MIDI_KANALER];
volatile int R_tid[MIDI_KANALER];
int ADSR_oppdatert;
extern
volatile float ADSR_CACHE[ENV_SIZE];
//ENV
volatile float ENV_mengde[MIDI_KANALER];
volatile int ENV_A_tid[MIDI_KANALER];
volatile int ENV_D_tid[MIDI_KANALER];
float ENV;
volatile float ENV_S[MIDI_KANALER];
int ENV_S_start[MIDI_KANALER];
volatile int ENV_R_tid[MIDI_KANALER];
extern volatile float ENV_CACHE[ENV_SIZE];
int ENV_oppdatert;
int k =0;
//KOEFFS
int Orden[MIDI_KANALER]={2,4,4,4};
int Filter_Res = 256;
int TAPS;
int c =0;
int r =0;
float
radius =0.0;
float PI =
3.14159265358979323846;
float
Omega0= 0.0;
float
Omega02 = 0.0;
float A =
0.0;
float AA =
0.0;
float B =
0.0;
float
BB=0.0;
float C =
0.0;
float Im = 0.0;
float Im2 = 0.0;
float G =
0.0;
float GG =
0.0;
float GGG =
0.0;
int Rez[MIDI_KANALER];
int
Cutoff[MIDI_KANALER];
int
filter_cnt=0;
//FILTER
extern
float filterbank[256][256][3];
float
b_coeffs[MIDI_KANALER][7];
float
a_coeffs[MIDI_KANALER][7];
float pm
a_tabell[7];
float pm b_tabell[7];
float tilstand[8];
float state[MIDI_KANALER][8];
float
output;
int MIDI;
//S&H
volatile int SH_mengde[MIDI_KANALER];
//NOISE
int noise;
int noise_mod;
volatile float Noise_mengde[MIDI_KANALER];
//Ringmod
float ringmod;
volatile float Ringmod_mengde[MIDI_KANALER];
//EFXsend
extern
volatile float left_direkte_sample;
extern
volatile float right_direkte_sample;
extern
volatile float left_delay_sample_input;
extern
volatile float right_delay_sample_input;
float left_delay_send[MIDI_KANALER];
float right_delay_send[MIDI_KANALER];
float left_direkte[MIDI_KANALER];
float right_direkte[MIDI_KANALER];
float left_delay_input[MIDI_KANALER];
float right_delay_input[MIDI_KANALER];
float left_REV_input[MIDI_KANALER];
float right_REV_input[MIDI_KANALER];
float left_REV_send[MIDI_KANALER];
float right_REV_send[MIDI_KANALER];
extern
volatile float left_REV_sample_input;
extern
volatile float right_REV_sample_input;
extern
volatile int Time1_val;
extern
volatile int Time2_val;
extern
volatile int Time3_val;
extern
volatile float Feedback_tap1_mengde;
extern
volatile float Feedback_tap2_mengde;
extern
volatile float Feedback_tap3_mengde;
extern
volatile float T1_pan;
extern volatile
float T2_pan;
extern volatile
float T3_pan;
extern volatile
float T1_mengde;
extern volatile
float T2_mengde;
extern volatile
float T3_mengde;
extern
volatile float Delay_to_REV;
//STEMME STRUKTUREN
struct voice_structure{
int note;
int periode; // NB!! periode er HELTALL!!
int frekvens;
int firkant_sample_cnt;
int sagtann_sample_cnt;
float sagtann_sample;
int MIDI;
int ADSR_cnt;
int ADSR_cache_index;
int ADSR_S;
float ADSR;
float ADSR_temp;
int ENV_cnt;
float ENV_temp;
float ENV;
int ENV_release_cnt;
int ENV_cache_index;
int lfo_cnt;
int lfo_oppdater_cnt;
int lfo_periode;
float lfo;
int release;
int release_cnt;
float release_temp;
int kill_queue;
float right_sample;
float left_sample;
int noise;
int impulse_cnt;
int impulse_update_cnt;
int sekvens;
int level;
float SH;
};
struct
voice_structure voice_queue[ANT_STEMMER]; //STEMME
KØ
extern float frekvens[98]; //FREKVENS OPPSLAG TABELLEN
int ep=0;
int MIDI_kanal_cnt=0;
extern int queue_index[MIDI_KANALER][98];
volatile int Oppdater=-1;
volatile int Oppdater_MIDI;
volatile int Oppdater_note;
int ta_bort;
//PAN
float
Pan[MIDI_KANALER];
//DMA
int dmabuf_adr;
volatile
int tx_ready;
volatile int Parameter_oppdater;
// TIMER
volatile int sample_tid;
/*--------------------------------------------------------------------------
FUNCTION PROTOTYPES
--------------------------------------------------------------------------*/
void
new_sample(int);
void lfo_oppdatering(int);
void
summer_osc(float);
void
adsr(int);
void
parameter_reload(void);
int
set_flag(int, int);
float
iir(float sample_in, float pm a_coeffs[], float pm b_coeffs[], float dm
state[], int taps);
void filter(int);
void filter_oppdatering(int);
void filterbank_oppdatering(void);
void ny_stemme(int, int);
void drep_stemme(int, int);
void
dequeue(int);
void
pan(int);
void
efx(int index);
void
summer_efx(void);
void
clear(void);
void
dma_init(void);
void
send_efx(void);
void
send_efx_sig(void);
void DMA_rx_handeler(int);
void DMA_tx_int_handeler(int);
void timer_int_handeler(int);
void timer_init(void);
void set_timer(int);
void filter_ENV(int);
void
initialisering(void);
void
lyd_algoritme_init(void);
void
parameter_update(void);
void
voice_update(void);
void
voice(void);
void
wait(void);
void housekeeping(void);
/****************************************************************************
****************************************************************************/
void ny_stemme(int MIDI_kanal, int note_nummer)
{
if(ep==ANT_STEMMER-1)dequeue(0); /*stemme overflow, eldste stemme blir fjernet for å gi plass til den nye */
MIDI=MIDI_kanal-1;
ep++;
voice_queue[ep].note = note_nummer;
voice_queue[ep].frekvens = frekvens[note_nummer];
voice_queue[ep].periode = sample_fq/frekvens[note_nummer];
voice_queue[ep].MIDI = MIDI; //blir KUN brukt til tabell oppslag
queue_index[MIDI_kanal-1][note_nummer] = ep;
voice_queue[ep].lfo_periode = lfo_sample_fq/Lfo_frekvens[MIDI];
voice_queue[ep].release_cnt = 0;
}
/* Drep_stemme tar imot notenummer og midikanal og finner ut hvilken index i stemmekøen
stemmen som skal slettes har. Derette kalles dequeue() som fjerner stemmen fra køen */
void drep_stemme(int MIDI_kanal, int note_nummer)
{
ta_bort = queue_index[MIDI_kanal-1][note_nummer];
queue_index[MIDI_kanal-1][note_nummer]=-1;
voice_queue[ta_bort].release=1;
voice_queue[ta_bort].ADSR_cnt=0;
ta_bort=-1;
}
/* dequeue fjerne riktig stemme fra stemmekøen og ordner køen etterpå */
void
dequeue(int index)
{
//if(index>ep)return -1;
while(index<ep)
{
voice_queue[index]=voice_queue[index+1];
index++;
}
ep--;
}
// KJØRES BARE HVER TIENDE PROGRAMGJENNOMKJØRING
void lfo_oppdatering(int index)
{
lfo_halv_periode = voice_queue[index].lfo_periode/2.0;
if(voice_queue[index].lfo_cnt == voice_queue[index].lfo_periode)voice_queue[index].lfo_cnt = 0;
if(voice_queue[index].lfo_cnt <
lfo_halv_periode)voice_queue[index].lfo
=2*voice_queue[index].lfo_cnt/((float)(voice_queue[index].lfo_periode));
else voice_queue[index].lfo =
-2*voice_queue[index].lfo_cnt/((float)(voice_queue[index].lfo_periode))+2;
voice_queue[index].lfo_cnt++;
voice_queue[index].noise =
rand()&(max_level-Forvrengning[MIDI]);
}
void
new_sample(int index)
{
firkant_periode = (int)(voice_queue[index].periode * Firkant_oktav[MIDI])+Firkant_fin[MIDI];
/* Firkant oscillator frekvens moduleres av sagtann oscillatoren. Dette blir gjort ved å forandre
periodetiden til oscillatoren. Dette blir derfor en negativ FM-modulasjon(p+dp = lavere frekvens) */
if(Firkant_FM_mengde[MIDI]>0.001)
{
if(sagtann_sample>=0)firkant_periode += ldexpf(voice_queue[index].sagtann_sample*Firkant_FM_mengde[MIDI]*firkant_periode,oktav-1);
else firkant_periode += ldexpf(voice_queue[index].sagtann_sample*Firkant_FM_mengde[MIDI]*firkant_periode,-oktav);
}
firkant_halv_periode = firkant_periode*PWM[MIDI];
if(voice_queue[index].firkant_sample_cnt==firkant_periode)voice_queue[index].firkant_sample_cnt=0;
if(firkant_halv_periode -
voice_queue[index].firkant_sample_cnt >= 0)firkant_sample=1;
else
firkant_sample = -1;
voice_queue[index].left_sample=firkant_sample*Firkant_mengde[MIDI];
voice_queue[index].firkant_sample_cnt++;
if(voice_queue[index].lfo_oppdater_cnt
== oppdater_lfo) /* lfo oppdatering*/
{
lfo_oppdatering(index);
voice_queue[index].lfo_oppdater_cnt=0;
lfo_oppdatert=1;
}
if(!lfo_oppdatert){voice_queue[index].lfo_oppdater_cnt++;lfo_oppdatert=0;}
summer_osc(voice_queue[index].left_sample);
/* GENERERE SAGTANN SAMPLE */
sagtann_periode = voice_queue[index].periode*Sagtann_oktav[MIDI]+Sagtann_fin[MIDI];
if(Sagtann_FM_mengde[MIDI]>1.001)
{
if(firkant_sample>=0)sagtann_periode += firkant_sample*sagtann_periode*Sagtann_FM_dybde[0][MIDI];
else sagtann_periode -= firkant_sample*sagtann_periode*Sagtann_FM_dybde[1][MIDI];
}
sagtann_halv_periode = sagtann_periode*Trekant[MIDI];
if(voice_queue[index].sagtann_sample_cnt
>= sagtann_periode)voice_queue[index].sagtann_sample_cnt = 0;
if(voice_queue[index].sagtann_sample_cnt
<= sagtann_halv_periode)
{
sagtann_sample =
(2.0*voice_queue[index].sagtann_sample_cnt/((float)sagtann_periode))-1.0;
voice_queue[index].sagtann_sample=sagtann_sample;
}
else sagtann_sample
=voice_queue[index].sagtann_sample +
(-1-voice_queue[index].sagtann_sample)*voice_queue[index].sagtann_sample_cnt/((float)(sagtann_periode));
voice_queue[index].sagtann_sample_cnt++;
sagtann_mod_sample=sagtann_sample*Sagtann_mengde[MIDI];
summer_osc(sagtann_mod_sample);
/* NOISE kode */
noise = rand() & 0x000007ff;
noise = noise*Noise_mengde[MIDI];
summer_osc(noise);
/* Ring modulator */
ringmod= sagtann_sample*(1+Ringmod_mengde[MIDI]*sagtann_sample); summer_osc(ringmod);
}
void
adsr(int index)
{
if(ADSR_oppdatert)
{
if(voice_queue[index].release)
{
voice_queue[index].ADSR=voice_queue[index].ADSR_temp*(1-(voice_queue[index].release_cnt/((float)(R_tid[MIDI]))));
voice_queue[index].release_cnt++;
if(voice_queue[index].ADSR<0.01){ta_bort=index;ADSR_oppdatert=0;}
}
else
{
if(voice_queue[index].ADSR_cnt<A_tid[MIDI])voice_queue[index].ADSR=voice_queue[index].ADSR_cnt/((float)(A_tid[MIDI]));
else
{
/* Hvis D : */
if(voice_queue[index].ADSR_cnt <=
S_start[MIDI])voice_queue[index].ADSR =
1+(((S[MIDI]-1)*(voice_queue[index].ADSR_cnt - A_tid[MIDI]))/((float)(D_tid[MIDI])));
}
}
ADSR_CACHE[voice_queue[index].ADSR_cache_index]=1-ADSR_mengde[MIDI]
+ ADSR_mengde[MIDI]*voice_queue[index].ADSR;
voice_queue[index].ADSR_cache_index++;
}
else
{ /* Hvis det er S er ADSR konstant */
if(!voice_queue[index].ADSR_cache_index==S_start[MIDI]
| voice_queue[index].release==1) //m.a.o hvis ikke S
{
voice_queue[index].ADSR=ADSR_CACHE[voice_queue[index].ADSR_cache_index];
voice_queue[index].ADSR_cache_index++;
}
}
}
/* filter_ENV ER IDENTISK MED adsr() BORTSETT FRA STEMME DEAKTIVERINGEN */
void filter_ENV(int index)
{
if(ENV_oppdatert)
{
if(voice_queue[index].release)
{
voice_queue[index].ENV=voice_queue[index].ENV_temp*(1-(voice_queue[index].ENV_release_cnt/((float)(ENV_R_tid[MIDI]))));
voice_queue[index].ENV_release_cnt++;
if(voice_queue[index].ENV<0.01)ENV_oppdatert=0;
}
else
{
if(voice_queue[index].ENV_cnt<ENV_A_tid[MIDI])voice_queue[index].ENV=voice_queue[index].ENV_cnt/((float)(ENV_A_tid[MIDI]));
else
{
/* Hvis D : */
if(voice_queue[index].ENV_cnt <= ENV_S_start[MIDI])voice_queue[index].ENV = 1+(((ENV_S[MIDI]-1)*(voice_queue[index].ENV_cnt - ENV_A_tid[MIDI]))/((float)(ENV_D_tid[MIDI])));
}
voice_queue[index].ENV_temp=voice_queue[index].ENV;
}
ENV_CACHE[voice_queue[index].ENV_cache_index]=1-ENV_mengde[MIDI]
+ ENV_mengde[MIDI]*voice_queue[index].ENV;
voice_queue[index].ENV_cache_index++;
}
else
{ /* Hvis det er S er ENV konstant */
if(!voice_queue[index].ENV_cache_index==ENV_S_start[MIDI]
| voice_queue[index].release==1) //m.a.o hvis ikke S
{
voice_queue[index].ENV=ENV_CACHE[voice_queue[index].ENV_cache_index];
voice_queue[index].ENV_cache_index++;
}
}
}
void
summer_osc(float sample)
{
oscsum_sample+=sample;
}
void
parameter_reload(void)
{
for(i=0;i<MIDI_KANALER;i++)S_start[i]=A_tid[i]+D_tid[i];
}
void
efx(int index)
{
left_delay_input[MIDI] +=
voice_queue[index].left_sample * left_delay_send[MIDI];
left_REV_input[MIDI] +=
voice_queue[index].left_sample * left_REV_send[MIDI];
left_direkte[MIDI] +=
voice_queue[index].left_sample * Gain[MIDI];
right_delay_input[MIDI] +=
voice_queue[index].right_sample * right_delay_send[MIDI];
right_REV_input[MIDI] +=
voice_queue[index].right_sample * right_REV_send[MIDI];
right_direkte[MIDI] +=
voice_queue[index].right_sample * Gain[MIDI];
}
/* Summer_efx summerer samplene til Delay og Rev. Disse blokkene har kun ett input sample */
void summer_efx()
{
for(i=0;i<MIDI_KANALER;i++)
{
left_delay_sample_input
+= left_delay_input[i];
left_REV_sample_input +=
left_REV_input[i];
left_direkte_sample += left_direkte[i];
right_delay_sample_input +=
right_delay_input[i];
right_REV_sample_input
+= right_delay_input[i];
right_direkte_sample += right_direkte[i];
}
}
void
clear(void)
{
left_delay_sample_input = 0.0;
left_REV_sample_input = 0.0;
left_direkte_sample = 0.0;
right_delay_sample_input =0.0;
right_REV_sample_input = 0.0;
right_direkte_sample = 0.0;
oscsum_sample=0.0;
}
/* filterbank_update() genererer filter-polene slik at et stabilt filter garanteres
Filter koeffisientene A, B og forsterkningen, G, lagres i en tredimensjonal tabell,
slik at de lett kan hentes ut av filter() funksjonen.
Totalt brukes 3*256^2 = 65325 minneplasser til tabellen (=antall pol-posisjoner). */
void filterbank_oppdatering(void)
{
for(r=0;r<Filter_Res;r++)
{
radius= r/255.0;
for(c=0;c<Filter_Res;c++)
{
if(c<128)
{
Omega0
= PI*c/255.0;
A=-2.0*radius*cosf(Omega0);
}
else
{
Omega0
= PI*(1.0-(c/255.0));
A
= 2.0*radius*cosf(Omega0);
}
AA = A*A;
Omega02 = Omega0*Omega0;
Im= 2.0*radius*sinf(Omega0); /* Henter ut polens imaginærdel */
Im2 = -1.0*Im*Im;
B = (Im2 - AA)/-4.0; /* Finner filterets B koeffisient*/
G = (1 + A + B)/4.0; /* Finner filterets enhets-forsterkning*/
filterbank[c][r][0] = G;
filterbank[c][r][1]
= A;
filterbank[c][r][2]
= B;
}
}
}
/* filter_update genererer filterkoeffisentene og legger dem inn i hver sin tabell.
Koeffisientene er nå på en form som brukes i iir() funksjonen.
Denne rutinen tar input fra panelet gjennom variablene Cutoff og Rez. */
void filter_oppdatering(int MIDI)
{
G =
filterbank[Cutoff[MIDI]][Rez[MIDI]][0];
A = filterbank[Cutoff[MIDI]][Rez[MIDI]][1];
B =
filterbank[Cutoff[MIDI]][Rez[MIDI]][2];
if(Orden[MIDI]==2)
{
b_coeffs[MIDI][2]=G;
b_coeffs[MIDI][1]=2.0*G;
b_coeffs[MIDI][0]=G;
a_coeffs[MIDI][1]=-A;
a_coeffs[MIDI][0]=-B;
}
if(Orden[MIDI]==4)
{
G = G*G;
b_coeffs[MIDI][4] = G;
b_coeffs[MIDI][3] = 4.0*G;
b_coeffs[MIDI][2] = 6.0*G;
b_coeffs[MIDI][1] = b_coeffs[MIDI][3];
b_coeffs[MIDI][0] =
b_coeffs[MIDI][4];
a_coeffs[MIDI][3] =
-2.0*A;
a_coeffs[MIDI][2] =
-1.0*(2.0*B + A*A);
a_coeffs[MIDI][1] =
-2.0*A*B;
a_coeffs[MIDI][0] =
-1.0*B*B;
}
if(Orden[MIDI]==6)
{
G = G*G*G;
b_coeffs[MIDI][6] = G;
b_coeffs[MIDI][5] = 6.0*G;
b_coeffs[MIDI][4] = 15.0*G;
b_coeffs[MIDI][3] = 20.0*G;
b_coeffs[MIDI][2] = b_coeffs[MIDI][4];
b_coeffs[MIDI][1] =
b_coeffs[MIDI][5];
b_coeffs[MIDI][0] =
b_coeffs[MIDI][6];
AA = A*A;
BB = B*B;
a_coeffs[MIDI][5] =
-3.0*A;
a_coeffs[MIDI][4] =
-1.0*(3.0*B + 3.0*AA);
a_coeffs[MIDI][3] =
-1.0*(6.0*A*B + A*AA);
a_coeffs[MIDI][2] =
-1.0*(3.0*AA + 3.0*BB);
a_coeffs[MIDI][1] =
-3.0*A*BB;
a_coeffs[MIDI][0] =
-1.0*B*BB;
}
}
/* filter() funksjonen henter ut DirekteformII filter
koeffisientene som brukes i iir() funksjonen. Den
er et tillegg til ANSI C biblioteket, og er
laget av ANALOG DEVICES. iir() er spesialskrevet til 21065L
prosessoren slik at den er omtrent like rask som om funksjonen
skulle vært skrevet i Assembler direkte. */
void filter(int index)
{
for(j=0;j<=Orden[MIDI];j++)
{
a_tabell[j]=a_coeffs[MIDI][j];
b_tabell[j]=b_coeffs[MIDI][j];
tilstand[j]=state[MIDI][j];
}
tilstand[MIDI+1]=state[MIDI][MIDI+1];
voice_queue[index].left_sample =
iir(voice_queue[index].left_sample, a_tabell, b_tabell, tilstand, Orden[MIDI]);
}
void
pan(int index)
{ /*samplene fra osc delen ble lagt i left_sample */
voice_queue[index].left_sample=voice_queue[index].left_sample*voice_queue[index].ADSR;
voice_queue[index].right_sample =
voice_queue[index].left_sample * Pan[MIDI];
voice_queue[index].left_sample =
voice_queue[index].left_sample *(1-Pan[MIDI]);
}
void
lyd_algoritme_init( void )
{
/* testparameter. Skal ikke være med hvis kotroll enheten fungerer */
ta_bort=-1;
ep=-1;
Oppdater=1;
Oppdater_MIDI=1;
Oppdater_note=53;
Parameter_oppdater=0;
tx_ready=1;
A_time[0]=1000;
D_time[0]=500;
S[0]=0.4;
R_time[0]=700;
Firkant_oktav[0]=1.0;
Firkant_fin[0]=0.0;
Firkant_mengde[0]=1000;
Firkant_FM_mengde[0]=0.0;
Sagtann_FM_mengde[0]=0.0;
PWM[0]=0.5;
Sagtann_oktav[0]=5.0;
Sagtann_fin[0]=0.0;
Sagtann_mengde[0]=0;
Oppdater = 1;
Oppdater_MIDI= 1;
Oppdater_note = 55;
ADSR=1.0;
ADSR_mengde[0]=0.0;
fyr=0;
lfo_oppdatering(0);
left_delay_send[0]=1.0;
right_delay_send[0]=1.0;
Parameter_oppdater=1;
Gain[0]=1.0;
Lfo_frekvens[0]=1000;
oppdater_lfo =10;
Rez[0]=75;
Cutoff[0]=100;
Pan[0]=0.5;
set_timer(5000);
for(i=0;i<MIDI_KANALER;i++)
{
for(j=0;j<96;j++)queue_index[i][j]=-1;
for(k=0;k<8;k++)state[i][k]=0;
}
}
void DMA_rx_handeler(int signal)
{
/* SPORTrx interrupt benyttes ikke */
}
void
dma_init(void)
{
asm("#include
<def21065l.h>");
asm("BIT CLR IMASK
SPT0I;"); /*masker DMA tx interrupt */
SetIOP(IIT0A,0x0000C000); /*DMA bufferets start adresse */
SetIOP(IMT0A,1); /*DMA adr.inkerment
=1*/
SetIOP(CT0A,6);
SetIOP(TDIV0,0x00270007);
SetIOP(TDIV0,0x001F0002); /* Serial CLK = 20MHz, Framesync = 1F;*/ /* resten settes opp ved Tx*/
interrupts(SIG_SPT0I,DMA_tx_int_handeler);
asm("BIT SET IMASK SPT0I;"); /*Åpner for DMA tx interrupt */
Parameter_oppdater=0;
}
void DMA_tx_int_handeler(int signal)
{
/* SPORTtx interrupt benyttes ikke */
}
void timer_init(void)
{
/* Sette opp timer 0 for lav prioritets timer */
asm("bit clr mode2
TIMEN0;");
interrupts(SIG_TMZ,
timer_int_handeler); /* Place the interrupt vector in the
pseudo-interrupt
table. The real
int
vector should point there */
asm("BIT
SET IMASK TMZLI;\
BIT CLR MODE2 INT_HI0 | INT_HI1;\
BIT SET MODE2 PWMOUT0 |
TIMEN0;");
}
void set_timer(int tid)
{
asm("BIT CLR MODE2 TIMEN0;"); /* Disable timer */
SetIOP(TPERIOD0, tid); /* Set timer period */
SetIOP(TPWIDTH0, 1); /* Set timer width to 1 */
asm("BIT SET MODE2 TIMEN0;"); /* Enable timer */
}
void timer_int_handeler(int sig_num )
{
set_timer(SAMPLE_TID); /* setter opp timerern på nytt*/
sample_tid=1;
}
void
send_efx(void)
{
asm("BIT CLR IMASK
SPT0I;"); /*masker DMA tx interrupt */
SetIOP(STCTL0,0);
SetIOP(IIT0A,0x0000C000); /* DMA bufferets start adresse */
SetIOP(IMT0A,1); /* DMA
adr.inkerment =1*/
SetIOP(CT0A,6);
asm("BIT SET IMASK
SPT0I;"); /* Åpner for DMA tx interrupt */
SetIOP(STCTL0,0x000465F1);
oscsum_sample=0.0;
tx_ready=0;
}
void
send_efx_sig(void)
{
if(Parameter_oppdater) /* Hvis nye effekt kontroll-signaler */
{
send_efx_sig();
Parameter_oppdater=0;
}
else
SetIOP(CPTOB,??); /* DMA bufferstørrelse, samples + kontroll signaler */
SetIOP(STCTL0,0x010005F3); /* Clear DEN_B */
SetIOP(STCTL0,0x011005F3); /* SDEN_B = 1 -> DMA overføring på DMA kanal B starter*/
}
void initialisering(void)
{
dma_init();
timer_init();
system_init();
filterbank_oppdatering();
filter_oppdatering(0);
}
void
voice_update(void)
{
if(Oppdater>-1)
{
if(Oppdater==0)drep_stemme(Oppdater_MIDI,Oppdater_note);
if(Oppdater==1)ny_stemme(Oppdater_MIDI, Oppdater_note);
if(Oppdater==2)filterbank_oppdatering();
if(Oppdater==4)ADSR_oppdatert=1;
Parameter_oppdater=1;
Oppdater=-1;
}
}
void
parameter_update(void)
{
if(filter_cnt==10)
{
filter_oppdatering(MIDI_kanal_cnt);
filter_cnt=0;
parameter_reload();*/
if(MIDI_kanal_cnt==MIDI_KANALER-1)MIDI_kanal_cnt=0;
else MIDI_kanal_cnt++;*/
}
}
void
voice(void)
{
for(i=0;i<=ep;i++)
{
MIDI = voice_queue[i].MIDI;
adsr(i);
filter_ENV(i);*/
new_sample(i);
filter(i);
pan(i);
efx(i);
}
summer_efx();
}
void
housekeeping(void)
{
filter_cnt++;
if(ta_bort!=-1){dequeue(ta_bort);ta_bort=-1;}
}
void
wait(void)
{
while(!sample_tid);
sample_tid=0;
while(!tx_ready);
/* DMA
klar? */
}
/****************************************************************************
****************************************************************************/
void main (
void )
{
initialisering();
for(;;)
{
voice_uptate();
parameter_update();
voice();
housekeeping();
wait();
send_efx();
}
}
/************************************************************************
*******************
E N D O F P R O G R A M D S P 1
*********************
************************************************************************/
DSP2
Kode
/**********************************************************************
**********************************************************************
----------------------------------------------------------------------------
INCLUDES
--------------------------------------------------------------------------*/
#include
<def21065l.h>
#include
<21060.h>
#include
<signal.h>
#include
<filters.h>
#include
<math.h>
#include
"1819regs.h"
#include
<stdlib.h>
/*--------------------------------------------------------------------------
KONSTANTER & MAKRO DEFINISJONER
----------------------------------------------------------------------------
*/
#define MIDI_KANALER 4
#define
CODEC_ISR_VECT 0X9001
#define BUFF_LEN 144000 //=3sek
#define
CIRCULAR_BUFFER(TYPE,DAGREG,name)\
TYPE *name;\
int
__length_##name;\
TYPE *__base_##name;
#define
BASE(name) __base_##name = name
#define
LENGTH(name) __length_##name
#define
CIRC_MODIFY(ptr, step)\
{ptr += step;\
if (ptr >= __length_##ptr +
__base_##ptr)\
{\
ptr = __base_##ptr;\
}\
else if (ptr < __base_##ptr)\
{ \
ptr = __base_##ptr;\
}}
#define
CIRC_READ(ptr, step, variable, memory)\
{variable = *ptr;\
CIRC_MODIFY(ptr, step);}
#define
CIRC_WRITE(ptr, step, variable, memory)\
{*ptr = variable;\
CIRC_MODIFY(ptr, step);}
#define
SetIOP(addr, val) (* (int *) addr) =
(val)
#define
GetIOP(addr) (* (int *) addr)
/*--------------------------------------------------------------------------
EKSTERNE DEKLARASJONER
-----------------------------------------------------------------------*/
/* HARDWIRET MED CODEC REGISTERENE */
extern volatile int user_tx_buf[6];
extern volatile int user_tx_ready;
extern volatile int user_rx_buf[6];
extern volatile int user_rx_ready;
/*--------------------------------------------------------------------------
GLOBALE DEKLARASJONER
--------------------------------------------------------------------------*/
//Delay
extern
float left_delay_buff[BUFF_LEN];
extern
float right_delay_buff[BUFF_LEN];
extern
volatile int Time1_val;
extern
volatile int Time2_val;
extern
volatile int Time3_val;
volatile
float tap1_left;
volatile
float tap2_left;
volatile
float tap3_left;
volatile
float tap1_right;
volatile
float tap2_right;
volatile
float tap3_right;
volatile
float fb1_left;
volatile
float fb2_left;
volatile
float fb3_left;
volatile
float fb1_right;
volatile
float fb2_right;
volatile
float fb3_right;
extern
volatile float Feedback_tap1_mengde;
extern
volatile float Feedback_tap2_mengde;
extern
volatile float Feedback_tap3_mengde;
volatile
float left_delay_output_sum;
volatile
float right_delay_output_sum;
volatile
float left_direkte_sample;
volatile
float right_direkte_sample;
volatile float
left_delay_sample_input;
volatile
float right_delay_sample_input;
//REV
extern
volatile float left_REV_sample_input;
extern
volatile float right_REV_sample_input;
extern
volatile float Delay_to_REV;
// PAN
extern volatile
float T1_pan;
extern volatile
float T2_pan;
extern volatile
float T3_pan;
// DMA
int dmabuf_adr;
extern volatile int Oppdatert;
/*--------------------------------------------------------------------------
FUNKSJON PROTOTYPER
--------------------------------------------------------------------------*/
void
delay(void);
void
delay_oppdater(void);
void
init(void);
void
sample_out(int,int);
void DMA_rx_handeler(int);
CIRCULAR_BUFFER(float,2,left_delay_ptr);
CIRCULAR_BUFFER(float,2,right_delay_ptr);
CIRCULAR_BUFFER(float,2,tap1_left_ptr);
CIRCULAR_BUFFER(float,2,tap2_left_ptr);
CIRCULAR_BUFFER(float,2,tap3_left_ptr);
CIRCULAR_BUFFER(float,2,tap1_right_ptr);
CIRCULAR_BUFFER(float,2,tap2_right_ptr);
CIRCULAR_BUFFER(float,2,tap3_right_ptr);
/*************************************************************************
**************************************************************************/
void delay_oppdater(void)
{
/*new_input_ptr'ene må initialiseres til 0 !!*/
tap1_left_ptr =left_delay_ptr -
Time1_val;
tap2_left_ptr =left_delay_ptr -
Time2_val;
tap3_left_ptr =left_delay_ptr -
Time3_val;
tap1_right_ptr=tap1_left_ptr;
tap2_right_ptr=tap2_left_ptr;
tap3_right_ptr=tap3_left_ptr;
}
/* pekerene er post-modify */
void
delay(void)
{
CIRC_READ(tap1_left_ptr,1,tap1_left,dm);
fb1_left = Feedback_tap1_mengde *
tap1_left;
left_delay_output_sum =
tap1_left*(1-T1_pan);
CIRC_READ(tap2_left_ptr,1,tap2_left,dm);
fb2_left = Feedback_tap2_mengde *
tap2_left;
left_delay_output_sum +=
tap2_left*(1-T2_pan);
CIRC_READ(tap3_left_ptr,1,tap3_left,dm);
fb3_left = Feedback_tap3_mengde *
tap3_left;
left_delay_output_sum +=
(tap3_left*(1-T3_pan)+left_direkte_sample);
left_delay_sample_input += (fb1_left
+ fb2_left + fb3_left);
CIRC_WRITE(left_delay_ptr,1,left_delay_sample_input,dm);
CIRC_READ(tap1_right_ptr,1,tap1_right,dm);
fb1_right = Feedback_tap1_mengde *
tap1_right;
right_delay_output_sum =
tap1_right*T1_pan;
CIRC_READ(tap2_right_ptr,1,tap2_right,dm);
fb2_right = Feedback_tap2_mengde *
tap2_right;
right_delay_output_sum +=
tap2_right*T2_pan;
CIRC_READ(tap3_right_ptr,1,tap3_right,dm);
fb3_left = Feedback_tap3_mengde *
tap3_right;
right_delay_output_sum +=
(tap3_right*T3_pan + right_direkte_sample);
right_delay_sample_input +=
(fb1_right + fb2_right + fb3_right);
CIRC_WRITE(right_delay_ptr,1,right_delay_sample_input,dm);
}
void
DMA_init(void)
{
dmabuf_adr =
(int)&left_delay_sample_input;
asm("#include
<def21065l.h>");
asm("BIT CLR IMASK SPR0I;"); /* masker DMA tx interrupt */
SetIOP(SRCTL0,0);
SetIOP(IIR0A,dmabuf_adr); /* DMA bufferets start adresse */
SetIOP(IMR0A,1); /* DMA adr.inkerment =1*/
SetIOP(CPR0A,6); /* DMA buffer størrelse (i 32bit ord)*/
SetIOP(SRCTL0,0x000421F1);
/* SDEN_A=1, RFSR=1, SLEN=1F (32-1), DTYPE=01, SPEN_A=1 */
interrupts(SIG_SPR0I,DMA_rx_handeler);
asm("BIT SET IMASK SPR0I;"); /* Åpner for DMA rx interrupt */
}
void init(void)
{
/* Setter opp 1819 stereo CoDec på EZ-LAB kortet */
asm("#include
<def21065l.h>");
interrupt(SIG_SPT1I,(void
(*)(int))CODEC_ISR_VECT);
asm("BIT
SET IMASK SPT1I;"); /* unmasker sport
interrupt */
BASE(left_delay_ptr) = left_delay_buff; /* Definerer sirkulær pekerene */
LENGTH(left_delay_ptr) = BUFF_LEN;
BASE(right_delay_ptr) = right_delay_buff
LENGTH(right_delay_ptr) = BUFF_LEN;
BASE(tap1_left_ptr) =
left_delay_buff;
LENGTH(tap1_left_ptr) = BUFF_LEN;
BASE(tap2_left_ptr) =
left_delay_buff;
LENGTH(tap2_left_ptr) = BUFF_LEN;
BASE(tap3_left_ptr) =
left_delay_buff;
LENGTH(tap3_left_ptr) = BUFF_LEN;
BASE(tap1_right_ptr) =
right_delay_buff;
LENGTH(tap1_right_ptr) = BUFF_LEN;
BASE(tap2_right_ptr) =
right_delay_buff;
LENGTH(tap2_right_ptr) = BUFF_LEN;
BASE(tap3_right_ptr) =
right_delay_buff;
LENGTH(tap3_right_ptr) = BUFF_LEN;
T1_pan=0.5;
T2_pan=0.5;
T3_pan=0.0;
Time1_val = 4800;
Time2_val = 9600;
Time3_val = 14400;
Feedback_tap1_mengde=0.4;
Feedback_tap2_mengde=0.4;
Feedback_tap3_mengde=0.0;
}
void DMA_rx_handeler(int signal)
{
dmabuf_adr = (int)&left_delay_sample_input;
asm("#include
<def21065l.h>");
asm("BIT CLR IMASK SPR0I;"); /* masker DMA tx interrupt */
SetIOP(SRCTL0,0);
SetIOP(IIR0A,dmabuf_adr); /* DMA bufferets start adresse */
SetIOP(IMR0A,1); /* DMA adr.inkerment =1*/
SetIOP(CPR0A,6); /* DMA buffer størrelse (i 32bit ord)*/
SetIOP(SRCTL0,0x000421F1);
/* SDEN_A=1, RFSR=1, SLEN=1F (32-1), DTYPE=01, SPEN_A=1 */
interrupts(SIG_SPR0I,DMA_rx_handeler);
asm("BIT SET IMASK
SPR0I;");
}
void
sample_out(int left_sample, int right_sample)
{
user_tx_buf[LEFT_CHANL] =
left_sample;
user_tx_buf[RIGHT_CHNL] =
right_sample;
user_tx_buf[TAG] = DOUT_TAG;
user_tx_ready = 1;
}
void
main(void)
{
init();
delay_oppdater();
Oppdatert=0;
for(;;)
{
idle(); /* venter på CoDec */
if(Oppdatert)
{
delay_oppdater();
Oppdatert=0;
}
delay();
sample_out((int)left_direkte_sample,(int)right_direkte_sample);
while(user_tx_ready); /*Venter på at DMA skal lese CoDec samples */
}
}
/***************************************************************
***********************E
N D O F P R G R A M D S P 2
************
***************************************************************/
Atmelkode
Hovedprogram, Main()
//* include files *////////////////////////
///////////////////////////////////////////
#include <stdio.h>
//* memory mapping - external devices *//
//////////////////////////////////////////
#define adc1 0xFF700000
#define adc2 0xFF600000
#define adc3 0xFF500000
#define adc4 0xFF400000
#define adc5 0xFF300000
#define adc6 0xFF200000
#define display 0xFF100000
#define
dspin 0xFFE00000
#define
dspout 0xFFF00000
#define button12 0xFFC00000
#define button3 0xFFD00000
/* USART 1 Control Registers ////////////
///////////////////////////////////////*/
#define control 0xFFFCC000 /*
W RS State: - */
#define mode 0xFFFCC004 /* R/W RS
State: 0 */
#define interrupt_enable 0xFFFCC008 /* W RS State: - */
#define interrupt_disable 0xFFFCC00C /* W RS State: - */
#define interrupt_mask 0xFFFCC010 /* R RS
State: 0 */
#define channel_status 0xFFFCC014 /* R RS
State: 0x18 */
#define receiver_holding 0xFFFCC018 /* R RS State: 0 */
#define transmitter_holding 0xFFFCC01C /* W RS State: - */
#define baud_rate_generator 0xFFFCC020 /* R/W RS State: 0 */
#define receiver_timeout 0xFFFCC024 /* R/W RS State: 0 */
#define transmitter_timeguard 0xFFFCC028 /* R/W RS State: 0 */
#define receive_pointer 0xFFFCC030 /* R/W RS State: 0 */
#define receive_counter 0xFFFCC034 /* R/W RS State: 0 */
#define transmit_pointer 0xFFFCC038 /* R/W RS State: 0 */
#define transmit_counter 0xFFFCC03C /* R/W RS State: 0 */
//* globale variables *//////////////////
/////////////////////////////////////////
int dma_c;
int display_c;
int p_store;
int part_c;
//* globale arrays */////////////////////
char temp_adc[48]
char dma_adc[48]
//* function prototypes *////////////////
/////////////////////////////////////////
//* normal functions *///////////////////
void arm_init();
void usart1_init();
void display_init();
void adc_init();
unsigned short adc_load();
void adc_sort();
unsigned short button_load();
void button_sort();
void param_sort();
boolean dma_param_compare();
int display_param_compare();
void temp_store();
void perm_store();
void partchange(int part_c);
void display_change();
void dma_transfer_setup();
void idle();
//* interrupt functions *//
midiinterrupt();
dma_send_interrupt();
dma_receive_interrupt();
adc_interrupt();
//* function definitions *////////////////
void
usart1_init();
{
/* ikke implementert */
}
void arm_init();
{
/* ikke
implementert */
}
void display_init();
{
/* ikke
implementert */
}
void adc_init();
{
/* ikke
implementert */
}
unsigned short adc_load();
{
for(i=0; i<7; i++)
{
temp_adc[i] = *adc1
}
for(i=0; i<7; i++)
{
temp_adc[i+7] = *adc2
}
for(i=0; i<7; i++)
{
temp_adc[i+15] = *adc3
}
for(i=0; i<7; i++)
{
temp_adc[i+23] = *adc4
}
for(i=0; i<7; i++)
{
temp_adc[i+31] = *adc5
}
for(i=0; i<7; i++)
{
temp_adc[i+39]
= *adc6
}
}
void adc_sort();
{
/* ikke
implementert */
}
unsigned short button_load();
{
button_row1
= *button12
button row2
= *button3
}
void button_sort();
{
/* ikke implementert */
}
void
param_sort();
{
/* ikke implementert */
}
int dma_param_compare();
{
/* ikke
implementert */
}
int display_param_compare();
{
/* ikke implementert */
}
void
temp_store();
{
/* ikke implementert */
}
void
perm_store();
{
/* ikke implementert */
}
void partchange(int part_c);
{
/* ikke
implementert */
}
void display_change();
{
/* ikke implementert */
}
void
dma_transfer_setup();
{
/* ikke implementert */
}
void
idle();
{
/* ikke implementert */
}
//* main function definition *////////////////
//////////////////////////////////////////////
void main()
{
usart1_init();
arm_init();
display_init();
adc_init();
adc_load();
adc_sort();
button_load();
button_sort();
param_sort();
dma_param_compare();
display_param_compare();
if(display_compare|dma_compare
= true)
{
temp_store();
}
if(p_store
= true)
{
perm_store();
}
if(part_c)
{
part_change();
}
if(display_c
= true)
{
display_change();
}
if(dma_c =
true)
{
dma_transfer_setup();
}
else
adc_load();
}
*/////////////////////////////////////
///// Interrupt functions() //////
//////////////////////////////////////
/////////////////////////////////////*
*///////////////////////////////////////////////////////////////////////////////////////////////////////
MIDI
interrupt kalles hver gang USART bufferet fylles.
Sekvensen
for "note on/off" er 1 statusbyte som gir "on/off" +
midikanal, deretter følger 2 databyte
som
først gir MIDI notenummer, deretter "velocity" d.v.s. anslag. Disse
verdiene legges inn i DMA
tabellen
som overføres sammen med resten av parameterene til DSP prosessor nr 1.
///////////////////////////////////////////////////////////////////////////////////////////////////////*
midi()
/*For MIDI algoritme impelementasjonen se ”MIDI Algoritme” punktet*/
MIDI algoritme, Midi()
#include <c:\green\ansi\stdio.h>
char st_test=0;
char d=0;
char midichan_byte=0;
char c=0;
char ch=0x0F;
char off=0x01; /*for
test purpose, should be 0x80*/
char on=0x02; /*for
test purpose, should be 0x90*/
int
stat_flag=0;
int note_on=0;
int note_off=0;
int midichan=0;
int databyte_count=0;
int datavalue=0;
int notenumber=0;
int velocity=0;
void usart_interrupt();
void stat_sub();
void midichannel();
void data_sub();
main()
{
while(d=0);
d=getchar();
if(d)
usart_interrupt();
}
void
usart_interrupt()
{
/* Mask
interrupt */
st_test =
d&off;
if(st_test
== off)
{
stat_flag++;
stat_sub();
}
else
if(stat_flag=1)
printf("no
statusbyte\n");
data_sub();
}
void
stat_sub()
{
if(d&on
> 1)
{
note_on
= 1;
note_off
= 0;
midichannel();
}
else
{
note_on
= 0;
note_off
= 1;
midichannel();
}
}
void
midichannel()
{
midichan_byte
= d&ch;
midichan =
(int)midichan_byte;
}
/* Unmask
USART interrupt
Return from interrupt */
void
data_sub()
{
databyte_count++;
datavalue =
(int)d;
if(databyte_count
= 1)
notenumber
= datavalue;
else
if(databyte_count == 2)
{
velocity
= datavalue;
databyte_count
= 0;
}
}
/*Return
from interrupt*/
·
Introduction
to Signal processing Orfanidis
ISBN-0-13-240334
·
Calculus
with Analytic Geometry Edwards
and Penney
ISBN-0-13-176728-3
·
Digital
Logic Design Hayes
·
ISBN-0-201-15461-7
·
The
Analysis and Design of Linear Circuits Rosa
ISBN
Matlab 5 for engineers Biran & Breiner
ISBN-0-201-36043-8
Regulering av dunamiske systemer 1 og 2 Haugen
ISBN-82-519-1407-8
ISBN-82-519-1407-8