- Bespalov-Talanov instability
- Propagation solitons
- Solitons in bistable cavity
- Solitons in confocal cavities
- Bespalov-Talanov instability
In optics spatial solitons are the particle-like inhomogeneties
of electromagnetic field. The most known example is a soliton of
Nonlinear Shrodinger Equation (NLS):
 (1)
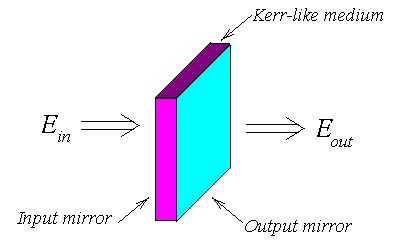
describing filaments occuring when light beam passes through
Kerr-like medium: dielectric, semiconductor, liquid, gas or even
vacuum. You can see below, how smooth laser beam coming from the
left passes through the Kerr medium. Bright spots in transverse
section appear after the passage, called filaments.
(1)
describing filaments occuring when light beam passes through
Kerr-like medium: dielectric, semiconductor, liquid, gas or even
vacuum. You can see below, how smooth laser beam coming from the
left passes through the Kerr medium. Bright spots in transverse
section appear after the passage, called filaments.
 Equation (1) is not easy to solve. Some authors found elegant
solutions. Among the most known are Bespalov and Talanov's result,
who found relation between width of filaments and speed of their growth.
According to their theory filaments originate from noisy harmonics:
Equation (1) is not easy to solve. Some authors found elegant
solutions. Among the most known are Bespalov and Talanov's result,
who found relation between width of filaments and speed of their growth.
According to their theory filaments originate from noisy harmonics:
 (2)
The first exponent is plane wave solution of Eq.1, while
(2)
The first exponent is plane wave solution of Eq.1, while
 is noisy modulation which leads to formation of the filaments.The
speed of the filaments growth, i.e.increments are given by:
is noisy modulation which leads to formation of the filaments.The
speed of the filaments growth, i.e.increments are given by:
 (3)
where
(3)
where  is inverse size of filament.The positive root
is inverse size of filament.The positive root  shows range of instability:
shows range of instability:
- Propagation solitons
Noteworthy, the above solution is valid for small modulations, thus for
linear stage of instability. Solitons are produced at nonlinear stage
of instability.For one transverse dimension the equation:
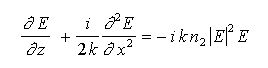 (6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
(6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
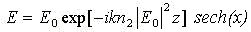
 The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
- Solitons in bistable cavity
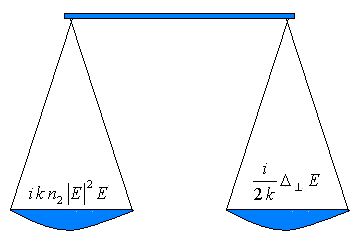
The existence of solitons is due to balance of diffraction and nonlinearity,
i.e. positive lens induced in Kerr medium by radiation:
 In dissipative systems this balance is accompanied by balance of gain
and losses.In optics examples are bistable cavity with external
light injection:
In dissipative systems this balance is accompanied by balance of gain
and losses.In optics examples are bistable cavity with external
light injection:
 and in bistable laser, i.e. laser with saturable absorber inside.
and in bistable laser, i.e. laser with saturable absorber inside.
Intracavity field exceeds incoming field and shows histeresis:
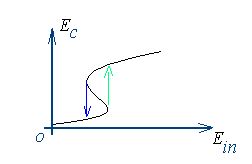 The above figure shows phenomenon of bistability: intracavity field
is multiple-value function of incoming field. The switching between
lower and upper branch of histeresis curve produces solitary waves,
which is referred to as autosolitons(See N.N.Rosanov).
The above figure shows phenomenon of bistability: intracavity field
is multiple-value function of incoming field. The switching between
lower and upper branch of histeresis curve produces solitary waves,
which is referred to as autosolitons(See N.N.Rosanov).
- Solitons in confocal cavities
Succesfully I found exact solution in for spatial soliton for a
specific case of bistable cavity.It is a cavity with a spherical
mirrors, whose foci are placed in the same point. Such confocal
microcavity contains thin gain and absorber slices, placed in
Fourier-conjugate planes, i.e. directly onto mirrors:
 The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
 (7)
and amplifying mirror(right) connected by Fourier transform:
(7)
and amplifying mirror(right) connected by Fourier transform:
 The solution hed been obtained by discrete map approach,
The solution hed been obtained by discrete map approach,
by means of asymptotic evaluation of nonlinear integral equation:
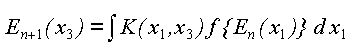 Notatons and definitions are in our recent paper.
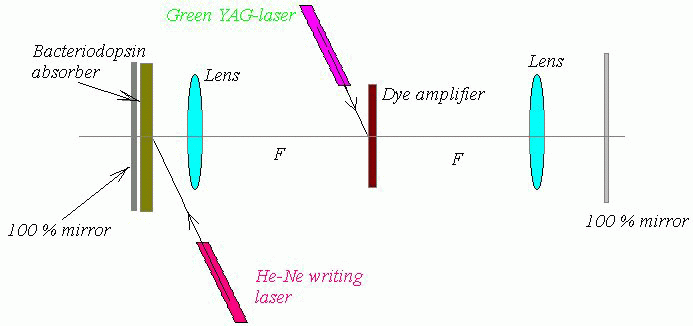
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
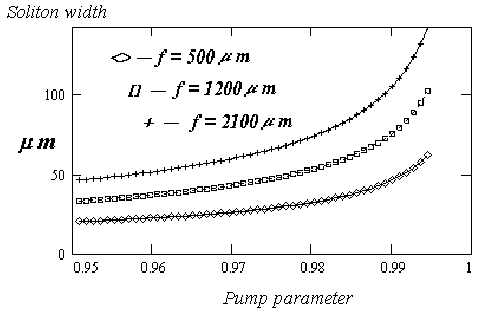
 The exact solution (7) gives, for example, correct description
The exact solution (7) gives, for example, correct description
of soliton width near lasing threshold:
This page is under construction.
Your request could stimulate completion of this page.
Please, send your comments to author.
In optics spatial solitons are the particle-like inhomogeneties of electromagnetic field. The most known example is a soliton of Nonlinear Shrodinger Equation (NLS):(1) describing filaments occuring when light beam passes through Kerr-like medium: dielectric, semiconductor, liquid, gas or even vacuum. You can see below, how smooth laser beam coming from the left passes through the Kerr medium. Bright spots in transverse section appear after the passage, called filaments.
Equation (1) is not easy to solve. Some authors found elegant solutions. Among the most known are Bespalov and Talanov's result, who found relation between width of filaments and speed of their growth. According to their theory filaments originate from noisy harmonics:
(2) The first exponent is plane wave solution of Eq.1, while
is noisy modulation which leads to formation of the filaments.The speed of the filaments growth, i.e.increments are given by:
(3) where
is inverse size of filament.The positive root
shows range of instability:

- Propagation solitons
Noteworthy, the above solution is valid for small modulations, thus for
linear stage of instability. Solitons are produced at nonlinear stage
of instability.For one transverse dimension the equation:
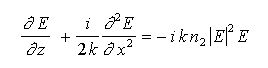 (6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
(6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
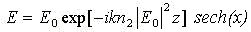
 The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
- Solitons in bistable cavity
The existence of solitons is due to balance of diffraction and nonlinearity,
i.e. positive lens induced in Kerr medium by radiation:
 In dissipative systems this balance is accompanied by balance of gain
and losses.In optics examples are bistable cavity with external
light injection:
In dissipative systems this balance is accompanied by balance of gain
and losses.In optics examples are bistable cavity with external
light injection:
 and in bistable laser, i.e. laser with saturable absorber inside.
and in bistable laser, i.e. laser with saturable absorber inside.
Intracavity field exceeds incoming field and shows histeresis:
 The above figure shows phenomenon of bistability: intracavity field
is multiple-value function of incoming field. The switching between
lower and upper branch of histeresis curve produces solitary waves,
which is referred to as autosolitons(See N.N.Rosanov).
The above figure shows phenomenon of bistability: intracavity field
is multiple-value function of incoming field. The switching between
lower and upper branch of histeresis curve produces solitary waves,
which is referred to as autosolitons(See N.N.Rosanov).
- Solitons in confocal cavities
Succesfully I found exact solution in for spatial soliton for a
specific case of bistable cavity.It is a cavity with a spherical
mirrors, whose foci are placed in the same point. Such confocal
microcavity contains thin gain and absorber slices, placed in
Fourier-conjugate planes, i.e. directly onto mirrors:
 The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
 (7)
and amplifying mirror(right) connected by Fourier transform:
(7)
and amplifying mirror(right) connected by Fourier transform:
 The solution hed been obtained by discrete map approach,
The solution hed been obtained by discrete map approach,
by means of asymptotic evaluation of nonlinear integral equation:
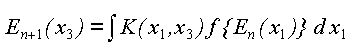 Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
 The exact solution (7) gives, for example, correct description
The exact solution (7) gives, for example, correct description
of soliton width near lasing threshold:

This page is under construction.
Your request could stimulate completion of this page.
Please, send your comments to author.
Noteworthy, the above solution is valid for small modulations, thus for linear stage of instability. Solitons are produced at nonlinear stage of instability.For one transverse dimension the equation:
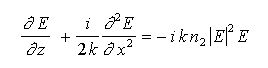 (6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
(6)
had been solved by V.E.Zakharov and A.B.Shabat exactly.
Among the solutions obtained the simplest is a single soliton:
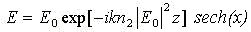
 The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
The soliton propagates without changing its shape until it find
inhomegeneity or another soliton.
The existence of solitons is due to balance of diffraction and nonlinearity, i.e. positive lens induced in Kerr medium by radiation:In dissipative systems this balance is accompanied by balance of gain and losses.In optics examples are bistable cavity with external light injection:
and in bistable laser, i.e. laser with saturable absorber inside.
Intracavity field exceeds incoming field and shows histeresis:The above figure shows phenomenon of bistability: intracavity field is multiple-value function of incoming field. The switching between lower and upper branch of histeresis curve produces solitary waves, which is referred to as autosolitons(See N.N.Rosanov).
- Solitons in confocal cavities
Succesfully I found exact solution in for spatial soliton for a
specific case of bistable cavity.It is a cavity with a spherical
mirrors, whose foci are placed in the same point. Such confocal
microcavity contains thin gain and absorber slices, placed in
Fourier-conjugate planes, i.e. directly onto mirrors:
 The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
 (7)
and amplifying mirror(right) connected by Fourier transform:
(7)
and amplifying mirror(right) connected by Fourier transform:
 The solution hed been obtained by discrete map approach,
The solution hed been obtained by discrete map approach,
by means of asymptotic evaluation of nonlinear integral equation:
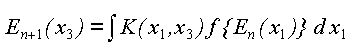 Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
 The exact solution (7) gives, for example, correct description
The exact solution (7) gives, for example, correct description
of soliton width near lasing threshold:

This page is under construction.
Your request could stimulate completion of this page.
Please, send your comments to author.
Succesfully I found exact solution in for spatial soliton for a specific case of bistable cavity.It is a cavity with a spherical mirrors, whose foci are placed in the same point. Such confocal microcavity contains thin gain and absorber slices, placed in Fourier-conjugate planes, i.e. directly onto mirrors:
 The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
The solution obtained has exact form of sech soliton for both
absorbing mirror(left):
 (7)
and amplifying mirror(right) connected by Fourier transform:
(7)
and amplifying mirror(right) connected by Fourier transform:
 The solution hed been obtained by discrete map approach,
The solution hed been obtained by discrete map approach,by means of asymptotic evaluation of nonlinear integral equation:
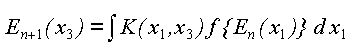 Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
Notatons and definitions are in our recent paper.
The above solution predicted akin spatial solitons observed in confocal
cavity with saturable absorber and in numerical experiment
performed by V.B.Taranenko,K.Staliunas,C.O.Weiss:
 The exact solution (7) gives, for example, correct description
The exact solution (7) gives, for example, correct descriptionof soliton width near lasing threshold:

This page is under construction. Your request could stimulate completion of this page. Please, send your comments to author.
