 |
 |
 |
 |
 |
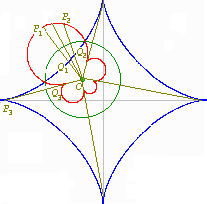
The blue curve is Astroid The Pedal Curve is the locus of the point P of intersection of the perpendicular (1,2,3,4) from the Pedal Point O to a Tangent (5, 6, 7, 8) to the Original Curve (Astroid in this example) Pedal Curve |
 |
|
Cartesian equation:
x2/3 + y2/3 = a2/3 or
(x2 + y2 - a2)3
+ 27a2x2y2 = 0
Parametrically equation: x = a cos3(t), y = a sin3(t), Area of Curve: 3pa2/8, Let's calculate the length of astroid L . xt' = -3a cos2(t) sin(t), yt' = 3a sin2(t) cos(t), (xt')2 + (yt')2 = (3a sin(t)cos(t))2 = (3a sin(2t)/2)2 L = 4ò 0p/2 Ö (xt')2 + (yt')2 = -4 * 3a/2 * 1/2 * cos(2t) ½0p/2 = -3a* (cos(p) - cos(0)) = 6a |
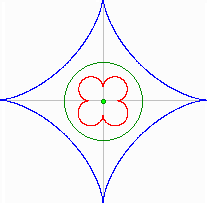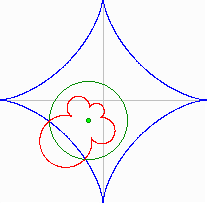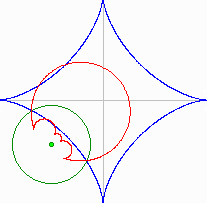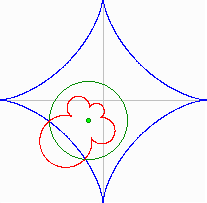 |
The Inverse Curve is the locus of the inverse point P Pi and Qi are inverse if OPi * OQi = r2 Points (Q1,Q2,Q3,Q4) belong to the Original Curve (here Astroid), (P1,P2,P3,P4) belong to the Inverse Curve |
 |
|
The first to investigate the curve was Roemer (1674).
Also Johann Bernoulli (1691) worked on the curve. Leibniz corresponded about the curve in 1715. |
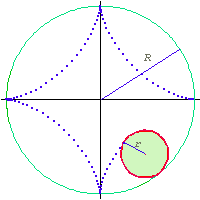 |
Astroid is defined as the trace of a point
on a circle of radius r rolling inside a fixed circle of radius 4 r or 4/3 r. The latter is known as double generation. |
 |
|
To see the clip
Astroid Trammel
in the format mov the Quick Time
Movie Viewer plug-in should be installed for your browser. |
 |
The length of tangent cut
by the axes is constant. A mechanical device where a fixed bar with endings sliding on two penpendicular tracks is called the Trammel of Archimedes |
 |
|
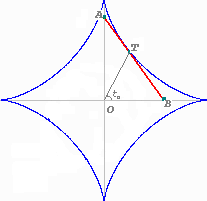
Let's T is the point of tangency
of tangent AB of astroid
and coordinates of point T are:
x0 = a cos3(t0), y0 = a sin3(t0). xt'(t0) = -3a cos2(t0) sin(t0), yt'(t0) = 3a sin2(t0) cos(t0). Derivation yx'(t0) = yt'(t0)/xt'(t0) = -tg(t0) and the equation of AB is: Point A: xB = 0 and yB = a cos3(t0)tg(t0) + a sin3(t0) = a sin(t0). Therefore, length of Trammel of Archimedes is a. |
|
Parametric equation of Hypotrochoid: x = (a - b)cos(t) + h cos((a/b - 1)t), y = (a - b)sin(t) - h sin((a/b - 1)t), Defenition of Hypotrochoid: If circle B (radus b) roll inside circle A (radius a) without slipping and Q is a point fixed on B (tracing point, distance from the Q to the center of circle B is h), then the traced curve is called hypotrochoid. Astroid is the case {1,1/4,1/4} of Hypotrochoid i.e. a/4 = b = h because x = a/4 (3cos(t) + cos(3t)) and cos(3t) = cos3(t) - 3 sin2t cos(t) ,i.e x = (a/4) 4cos3(t) y = a/4 (3sin(t) - sin(3t)) and sin(3t) = 3 cos2(t)sin(t) - sin3t , i.e. y = (a/4) 4sin3(t) In the same way Astroid is the case {1,3/4,3/4} of Hypotrochoid i.e. a/4 = b = h |

|
To see next famous clips in the format mov the Quick Time Movie Viewer plug-in should be installed for your browser. Astroid Generation (format mov) Hypotrochoid (format mov) For more details see many Hypotrochoid Examples Or Hypotrochoid Java Applet |

|
|
Parametric equation of Epitrochoid: x = (a + b)cos(t) + h cos((a/b + 1)t), y = (a + b)sin(t) + h sin((a/b + 1)t) Defenition of Epitrochoid: If circle B (radus b) roll around circle A (radius a) without slipping and Q is a point fixed on B (tracing point, distance from the Q to the center of circle B is h), then the traced curve is called epitrochoid. Cardioid is the case {1,1,1} of Epitrochoid i.e. a = b = h. Therefore, parametric equation of Cardioid: x = 2a cos(t) + a cos(2t)) = 2a cos(t)(1+cos(t)) - 2a y = 2a sin(t) + a sin(2t)) = 2a sin(t)(1+cos(t)) From this the polar equation of the Cardioid: r(t) = 2a (1 + cos(t)). |
|
Hypotrochoid and epitrochoid are roulette of two circles. If one circle is inside another, the curve traced are called hypotrochoids. Otherwise (one rolls outside another), the curves are called epitrochoids. If the tracing point is on the (circumference) rolling circle, the curves are called hypocycloid or epicycloids. |
 |
For any chord passes through cusp
of a cardioid, the sum of distances
from the cusp to the intersections is equal to the diameter of the cardioid. Really, this sum is equal r(t) + r(t + p) = 2a(1+cos(t)) + 2a(1+cos(t+p)) = 4a, because cos(t) + cos(t + p)) = 0; Cardiod Perimeter and Area Cardiod Generation(format mov) Special Plane Curves:Cardioid A Visual Dictionary of Special Plane Curves |
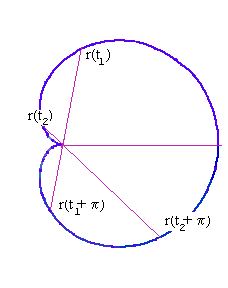 |
|
A tangent direction is given by the
yx' = yt' / xt' =
(2a sin(t)(1+cos(t))' / (2a cos(t)(1+cos(t))' =
(cos(t) + cos(2t))/(sin(t) + sin(2t)). If yx' = k, then cos(t) - k sin(t) + cos(2t) - k sin(2t) = 0. Let's k = tg(a), then cos(t + a) + cos(2t + a) = 0. Therefore, 2cos(3t/2 + a) cos(t/2) = 0, 3t/2 + a = p/2 + p n, t = 2pn/3 + (p/3 - a). On the other words a tangent direction is repeating every 2p/3. Given any direction, there are exactly three tangents parallel to it. If we connect the points of tangency to the cusp, the three segments meet at equal angles of 2p/3. |
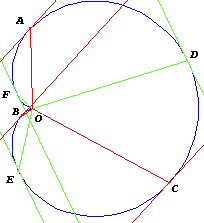
| Three parallel red tangents have
the points of tangency A, B, C. So, angles
AOB, BOC, COA
are equal angles of 2p/3. O is the casp point of cardioid. Three parallel green tangents have the points of tangency D, E, F. So, angles DOE, EOF, FOD are equal angles of 2p/3. |
 |
Since cos(x) + cos(y) =
2cos((x+y)/2)cos((x-y)/2) then cos(a+2p/3))+ cos(a+4p/3))= 2cos(a+p)cos(p/3)= cos(a+p)= -cos(a). Hence,, sum of distances AO+BO+CO (or DO+EO+FO) is equal to 2a(1+cos(a))+ 2a(1+cos(a+2p/3))+ 2a(1+cos(a+4p/3)) = 6a for every a. |
|
Parametric equation of hypocycloid x = (a - b)cos(t) + b cos((a/b - 1)t), y = (a - b)sin(t) - b sin((a/b - 1)t), Hypocycloid is the hypotrochoid for b = h. Parametric equation of epicycloids: x = (a + b)cos(t) + b cos((a/b + 1)t), y = (a + b)sin(t) + b sin((a/b + 1)t), Epicycloid is the epitrochoid for b = h. |
|
THE EPICYCLOID Curve Family Index An epicycloid with some cusps | 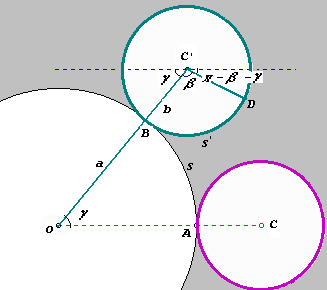
|
|
How to get epicycloid equation? Circle 1 (center C,radius b) roll around circle 2 (center O,radius a), point A moved to the point B, point B moved to the point D. Point C' moved to the point C'. So, the point D has coordinates respecting the center C'.On the other hand point C' has coordinates respecting the center O. Hence, point D has coordinates respecting the center O. Let's found b . The arc length traced by point D is equal to the distance circle 2 rolles around circle 1: Therefore, D has coordinates: In the same way coordinates of point on the hypocycloid are |
|
If a = b for epicycloid we get equation
of the cardioid: |
If b = a/4 for hypocycloid we get equation
of the astroid: |
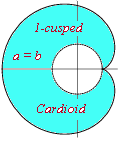 |
1-cusped epicycloid
r = 2a (1 + cos(g )) x = 2a cos(g ) + a cos(2g ) y = 2a sin(g ) + a sin(2g ) It's not difficalt to calculate that cartesian equation is: (x2 + y2 - 4 a x)2 = 4 a2(x2 + y2) |
 |
2-cusped epicycloid
r = x = 3a cos(g ) + a cos(3g ) y = 3a sin(g ) + a sin(3g ) Cartesian equation: (x2 + y2 -4 a2)3 = 108 a4y2 |
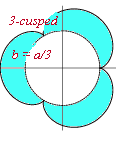 |
3-cusped epicycloid
r = x = 4a cos(g ) + a cos(4g ) y = 4a sin(g ) + a sin(4g ) |
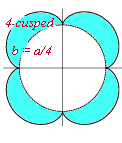 |
4-cusped epicycloid
r = x = 5a cos(g ) + a cos(5g ) y = 5a sin(g ) + a sin(5g ) |