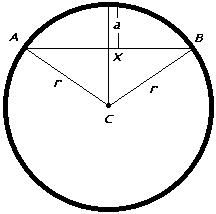
Distance between points A and B is b.

Distance between points A and B
is b.
radius² = (a/2)²
+ (radius-x)²
radius = x/2 + a²/8r
2. You want to prove the Half-of-perimeter-to-radius ratio for circle is pi.
A circle is a polygon with infinite number of side.
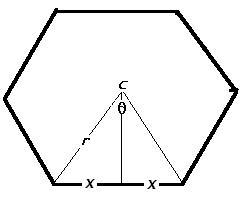
If the hexagon( sides = 6) above changed so that number of sides eventually
become infinite then
the geometry becomes a circle.
Ø = 360°/n
x = r * sin(Ø/2)
side = 2 * x = 2*r*sin(Ø/2) = 2*r*sin(180°/n)
Perimeter = n * side = 2*n*r*sin(180°/n)
Perimeter-to-radius ratio = 2*n*sin(180°/n)
When n =3
Half-of-Perimeter-to-radius-ratio = 3*sin(180°/3) = 6/sqrt(3) =
2.5980
when n = 4(square)
Half-of-Perimeter-to-radius-ratio = 4*sin(180°/4) = 4/sqrt(2) =
2.8284
when n = 32
Half-of-Perimeter-to-radius-ratio = 32*sin(180°/32) = 3.1365
when n = infinity
Limit
n*sin(180°/n)
n->infinity
Applying following rule:
u(x) * v(x) = u´(x) * v(x) + v´(x) * u(x)
Half-of-Perimeter-to-radius-ratio =
Limit
n*cos(180°/n)*180°/n + 1 * sin(180°/n) = 1*180°+0
= pi
n->infinity