Recursion

This page last updated October 19, 2003

Back to Bill Alexander's main web page

This lecture is located at http://geocities.datacellar.net/BillAlexander/recursion_lecture.html

Definition

Recursion is a process or function defined in terms of itself.

re·cur·sion n.: See Recursion.

Example 1: Factorial

A simple mathematical example of recursion is the factorial.

A factorial is generally defined as:

n! = n * (n-1) * (n-2) * … * 2 * 1

Or in recursive terms:

n! = n * (n-1)! where n > 0 and 1! = 1

C++ Factorial Example (see http://geocities.datacellar.net/BillAlexander/Factorial.cpp)

In C++, we could define the factorial class as follows:

class Factorial

{

public:

unsigned int Iterative (unsigned int n);

unsigned int Recursive (unsigned int n);

};

In the Factorial class, I have defined the two member functions: Iterative( ) and Recursive ( ).

Factorial::Iterative( ) performs an iterative calculation of the factorial. It is defined as follows:

unsigned int Factorial::Iterative (unsigned int n)

{

int ret;

int i;

// Check for 0

if (n == 0)

return 1;

// Initialize return value to n

ret = n;

// Calculate the factorial

for (i=n-1; i>1; i--)

{

ret *= i;

}

return ret;

}

Factorial::Iterative( ) takes the parameter n and calculates n * (n-1) * (n-2) * … * 2 * 1. It is a very simple function.

The Factorial::Recursive( ) member function, on the other hand, calculates the factorial in the recursive manner:

unsigned int Factorial::Recursive (unsigned int n)

{

// Are we at the end of the recursive factorial?

if (n <= 1)

{

// Yes -- terminate the calculation

return 1;

}

else

{

// No -- continue recursive calculation

return n * Recursive (n-1);

}

Factorial::Recursive( ) takes the parameter n can calculates n * (n-1)! This also is a very simple function.

The reason I have defined both an iterative and recursive function is to demonstrate the differences between the two processes. Both functions are simple, but the Factorial::Recursive( ) is simpler and easier to understand. This is one of the great strengths of recursion.

Example 2: The Fibonacci Sequence

A second mathematical example of recursion is the Fibonacci sequence:

1 1 2 3 5 8 13 21 34 55 …

Or

F(n) = 1 for n <= 2

F(n-2) + F(n-1) for n > 2

This is more complex than the factorial, but demonstrates both the strengths and weaknesses of recursion.

C++ Fibonacci Example (see http://geocities.datacellar.net/BillAlexander/Fibonacci.cpp)

In C++, we could define the Fibonacci class as follows:

class Fibonacci

{

public:

unsigned int Iterative (unsigned int n);

unsigned int Recursive (unsigned int n);

};

Just as with the factorial example, I have defined the two member functions Iterative( ) and Recursive ( ):

unsigned int Fibonacci::Iterative (unsigned int n)

{

unsigned int i;

unsigned int n_minus_2; // value of n-2 term

unsigned int n_minus_1; // value of n-1 term

unsigned int nth; // value nth term

// Check for 1st 2 terms

if (n <= 2)

return 1;

// Calculate the Fibonacci nth term

n_minus_2 = 1;

n_minus_1 = 1;

for (i=2; i<n; i++)

{

// The value of the nth term is the value of n-2 term + value of n-1 term

nth = n_minus_2 + n_minus_1;

// Update n-2 and n-1 terms for next term calculation

n_minus_2 = n_minus_1;

n_minus_1 = nth;

}

// Return the nth term calculation

return nth;

}

unsigned int Fibonacci::Recursive (unsigned int n)

{

// Are we at the end of the recursive Fibonacci?

if (n <= 2)

{

// Yes -- terminate the calculation

return 1;

}

else

{

// No -- continue recursive calculation

return Recursive(n-2) + Recursive(n-1);

}

As with the factorial example, the Recursive( ) member function is simpler , easier to understand , elegant and beautiful. However, the Fibonacci example also reveals the dark side to recursion: inefficient use of system resources.

System Resource Comparison Between Fibonacci::Iterative( ) and Fibonacci::Recursive( )

What I mean by “system resources” in this lecture is:

CPU usage

Memory usage (stack, heap, etc)

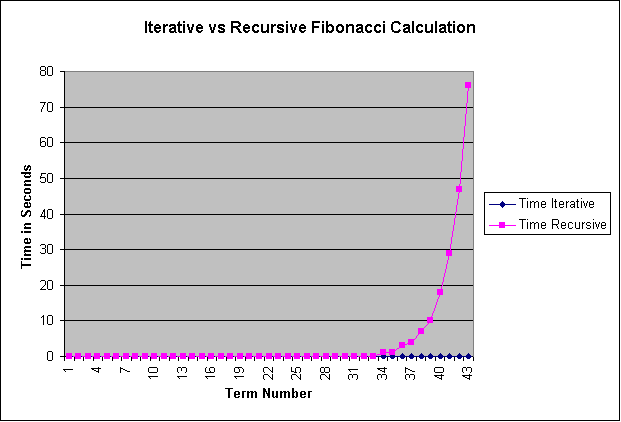
Let’s start with CPU usage. If we execute Fibonacci::Iterative(43) and Fibonacci::Recursive(43), we will immediately notice that the recursive method takes much longer to execute. On my 1.6 GHz laptop, Fibonacci::Iterative(43) executes in a blink of an eye, whereas, Fibonacci::Recursive(43) takes a whopping 76 seconds! Below is a graph of various values used for both the iterative and recursive methods (see http://geocities.datacellar.net/BillAlexander/fib_calc.html):

One reason for the inefficiency of Fibonacci::Recursive( ) is that many operations are repeated. We can see these repeated operations by examining the recursion tree of Fibonacci::Recursion(6):

In the above diagram, we abbreviate Fibonacci::Recursive(n) as F(n). With F(6), we see that F(1) is called 3 times, F(2) is called 5 times, F(3) is called 3 times, F(4) is called 2 times and F(5) is called once. For very large values of n, the repeated function calls are so numerous, that the calculation is doing mostly repeated work. Thus, you should use the iterative version of the Fibonacci calculator for a truly useful application.

Another consideration with recursion is the depth in which the calculation traverses on the stack. A stack is a special piece memory used by a program to store the function parameters, function return addresses and function local variables. As a recursive calculation descends to further levels, more and more memory is required. If a recursive function is not written carefully, it can crash an application’s stack and generate a protection fault in the system.

The above Fibonacci recursion tree shows that F(6) recurses down 4 levels. In general, F(n) will recurse down n-2 levels. For example, F(100) will recurse down 98 levels! This is probably not cause a problem on our standard PCs today, but certain applications may have trouble. Embedded systems, for example, generally have a limited amount of memory and recursing down 98 levels may cause a protection fault.

The inefficient use of system resources in the Fibonacci example does not mean that all recursion is inefficient. You must think about the algorithm and how it affects the system.

A solution to resource inefficiency is to use an optimizing compiler which detects recursion and generate iterative code instead. This has the advantage of being both elegant and efficient (see http://www.csi.uottawa.ca/~holte/T26/efficient-rec.html).

Another solution to the inefficiency problem is stackless recursion (see http://www.olympus.net/personal/7seas/recurse.cpp, Stackless Factorial). Basically, you write the function so that you limit the amount of recursion that occurs.

General Recursion Programming Rules:

Rule1: Always make sure to terminate the recursion. This is often referred to as the “Base Case”.

Example of what not to do:

int Fibonacci::Recursive (int n)

{

return Recursive (n-2) + Recursive (n-1);

}

This will never end because there is no base case to terminate the calculation.

Rule 2: Always subdivide the recursion into smaller pieces. This leads to the base case and thus will terminate the recusion.

Example:

double Bigger::Recursion (double n)

{