This a HTML version of a 12 page pamphlet with a
large fold-out illustration.
A copy is used that originates from the Stadtarchiv Friedberg i.d. Wetterau (Hessen) Ueber den
Gebrauch und die Einrichtung
des vor kurzem erfundenen
Planimeters
von dem
Professor G. Wagner.
Mit einer litographischen Abbildung
Frankfurt a. M. 1821.
In der Jägerschen Buch- Papier- und Landkartenhandlung.
Vorwort
Bei den wesentlichen Vortheilen, welche das von mir
erfundene Planimeter dem praktischen Geometer gewährt, hielt ich es
für zweckmäßig, theils für diejenigen, welche sich des
Instrumentes bedienen wollen, theils für den Mechaniker, welcher in dem
Fall ist, es ohne Original anfertigen zu müssen, eine kleine Abhandlung
über die Einrichtung und den Gebrauch desselben zu schreiben und dieser
eine genaue
Abbildung des Instruments beizufügen.
Die ersten Muster-Instrumente haben die geschickten Mechaniker,
herren Tomschitz und Olf zu Frankfurt a. M.
für die Königl. Preuß. General-Direktion
des Katasters, unter meinen Augen und so zu meiner Zufriedenheit angefertigt,
daß ich ihre Arbeit in jeder Hinsicht mit Ueberzuegung empfehlen kann.
Der Verfasser.
- Das Planimeter ist ein Instrument, durch welches
der Inhalt einer, in verjüngtem Maaßstabe geometrisch aufgetragenen
Fläche, ohne Zirkel und ohne Rechnung gefunden werden kann. Die bis jetzt
damit gemachten Versuche geben folgendes wichtige Resultat: 1) Die
Genauigkeit des Planimeters ist durch die Berechnung mit Zirkel und
Maaßstab nur schwer zu erreichen. 2) Die Pläne bleiben viel
sauberer und werden weder
durch Zirkelrisse noch durch das Einsetzen des Zirkels in die Punkte verdorben.
3) Die Arbeit gewinnt an Zuverlässigkeit unendlich, indem alle Fehler
und Irrthümer vermieden werden, welche durch das Abgreifen der Maaße
und durch das Rechnen entstehen können. 4) Endlich wird die Arbeit um
mehr denn das Doppelte gefördert, indem ein fleißiger Arbeiter, bei
einiger Fertigkeit im Gebrauch des Instruments, täglich 6 - 800
Trapezien mißt, wozu auch der fleißigste Rechner wenigstens
2 - 3 Tage gebrauchen würde.
- Die Konstruktion dieses Instrumentes beruht auf der
Lehre von den geometrischen Proportionen.
In den beiden ähnlichen rechtwinkelichten Dreiecken
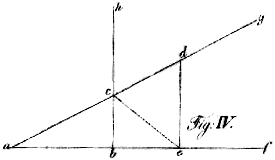 a b c und a e d
(Fig. IV.) ist
bc:ab=ed:ae, folglich
ed.ab=bc.ae. Der Inhalt des Dreiecks
a e c ist also
= ½ de.ab und da nun jede auf
a f errichtete senkrechte Linie mit den beiden
Schenkeln a g und
a f ein Dreieck bildet, welches
a b c ähnlich ist, so ist eine solche, multiplizirt
mit ½ a b auch allemal das Maaß eines
Dreiecks welches b c
zur Höhe und die Entfernung der Senkrechten von a, zur
Grundlinie hat. Ebenfalls werden alle auf a f
errichtete Senkrechte durch alle
Diagonale, welche aus a durch b h
gehen, proportionirt geschnitten, und es folgt also hieraus der allgemeine
Satz:
a b c und a e d
(Fig. IV.) ist
bc:ab=ed:ae, folglich
ed.ab=bc.ae. Der Inhalt des Dreiecks
a e c ist also
= ½ de.ab und da nun jede auf
a f errichtete senkrechte Linie mit den beiden
Schenkeln a g und
a f ein Dreieck bildet, welches
a b c ähnlich ist, so ist eine solche, multiplizirt
mit ½ a b auch allemal das Maaß eines
Dreiecks welches b c
zur Höhe und die Entfernung der Senkrechten von a, zur
Grundlinie hat. Ebenfalls werden alle auf a f
errichtete Senkrechte durch alle
Diagonale, welche aus a durch b h
gehen, proportionirt geschnitten, und es folgt also hieraus der allgemeine
Satz:
Der Inhalt eines jeden Dreiecks ist in dem Maaße einer
Senkrechten enthalten, welche auf e (dem Endpunkt der Grundlinie)
errichtet, durch eine aus a (dem Anfangspunkt der
Grundlinie) über die aus b (einem auf der Grundlinie
willkührlich angenommenen Punkte) senkrecht aufgetragene Höhe der
Figur gehende Diagonale geschlossen, und mit
½ ab multiplizirt wird.
Hat man also ein Instrument welches an die Grundlinie eines
Dreiecks sich anschließend, die Höhe desselben, aus einem auf der
Grundlinie beliebig angenommenen Punkte b senkrecht aufträgt,
hat man einen Mechanism, welcher aus a (dem Anfangspunkt der
Grundlinie) eine Diagonale über diesen Höhepunkt bildet, und hat man
endlich einen Maaßstab, welcher sich zu dem der Figur verhält wie
½ ab zu 1 und welcher auf der Grundlinie
bis zu dem Endpunkte derselben senkrecht fortbewegt werden kann, so ist die
Aufgabe leicht zu lösen, den Inhalt eines Dreiecks ohne Zirkel und
ohne Rechnung zu finden.
Nach diesen Verhältnissen und Bedingungen ist das Fig.
I.
abgebildete Planimeter konstruirt, zu dessen näherer Beschreibung ich
nun übergehe.
- Die Kante K L, an dem Triangel
I K L, welche sich an O P
senkrecht und mit A D parallel auf und nieder
bewegt, dient dazu, vermittelst des Punktes C die Höhe der zu
messenden Figur senkrecht über b (Fig.
IV) zu tragen, welches dadurch geschieht, daß
man, A auf a,
A D über
a e anlegt und
K L über den Höhepunkt der Figur richtet. Da
nun alle Senkrechte zwischen Parallelen gleich sind, und C von der
unteren Kante des Randes K L eben so weit absteht
als E F von der unteren Kante des Randes
A D, ferner eine aus C auf
A D fallende Senkrechte allezeit auf B
trifft, so mißt selbige nicht nur die Höhe der Figur, sobald
K L ihren Höhepunkt durchschneidet, sondern
trägt diese Höhe auch senkrecht über B, welches den
in Fig. IV angenommenen Punkt b
bezeichnet, C ist daher nach
§2
der beständige Durchschnittspunkt einer Diagonale, welche von dem, den
Anfang der Grundlinie bildenden Punkte E ausgeht und durch das um
C sich bewegende Lineal M N
gebildet wird, indem man dieses bis zu der senkrechten Kante E,
des auf B liegenden Vorsprungs
E Q umdreht.
Der Triangel H F G
enthält auf dem Rande F H
einen, auf die Entfernung des Punktes B von E (in
Fig. IV b von a)
berechneten Flächenmaaßstab, gleich dem Maaßstab der Figur
mulitplizirt mit ½E B. Wäre nun
E B angenommen zu 20 Ruthen, so gaben
10 Ruthen auf dem Maaßstabe der Figur schon
20/2×10=100
Ruthen auf dem Maaßstabe des Instruments und 100 Ruthen auf dem
Maaßstab der Figur gäben auf dem Maaßstabe des Instruments
20/2×100=1000
Ruthen u.s.w.
- Man sieht hieraus, daß die Entfernung des
Höhenpunktes B von E zwar willkührlich ist, es
wird aber, nach dem für den Flächenmaaßstab daraus entstehenden
Verhältnis, dieser um so größer je kleiner
E B
und wiederum desto kleiner je größer
E B angenommen wird.
Daraus geht aber auch zugleich hervor, daß man den Inhalt ganz kleiner und
ganz großer Figuren nicht füglich mit einem und demselben
Instrumente messen kann. Denn wenn der Flächenmaaßstab die
Größe has daß der Inhalt solcher Figuren, welche mehrere 100
bis 1000 Ruthen und drüber enthalten bis auf eine halbe Ruthe richtig
abgeschätzt werden kann, so ist diese Genauigkeit schon hinreichend, indem
man bei der Berechnung mit Zirkel und Maaßstab dem wahren Inhalt einer
Figur selten bis auf
1/400
nahe kommt. Bei kleineren Figuren dagegen wird schon eine größere
Genauigkeit gefordert und man muß also bei diesen ein solches Instrument
anwenden, an welchem die Entfernung des
Höhenpunktes B von E so gering und demzufolge der
Flächenmaaßstab so groß ist, daß man den Inhalt bis auf
1/10
Ruthe abschätzen kann. Es würde zwar eine solche Genauigkeit auch bei
größeren Figuren nicht überflüssig sein, dann aber
müßte ein Maaßstab von 1000 Ruthen schon eine
Ausdehnung erhalten, die den Gebrauch des Instrumentes ungemein erschwerte,
und doch dürfte er nicht weniger umfassen , weil Dreiecke von dieser und
noch größerer Dmension in der praktischen Geometrie haüfig
vorkommen.
Eine besondere Abbildung von einem solchen kleineren Instrumente
zu liefern, habe ich nicht für nöthig erachtet. Die Konstruktion
beider ist im Wesentlichen dieselbe; nur hat das kleinere bei einer geringeren
Entfernung des Höhenpunktes von E einen größeren
Maaßstab, und ist dadurch, daß der Schenkel
P D im Verhältnis zu
O P sehr lang und das ganze Instrument merklich
kleiner ist, hauptsächlich für kleinere Dreiecke und einzelne
Ackerstücke berechnet, welche großentheils bei einer geringen
Breite unverhältnißmäßig lang
sind. Die Ausdehnung beider wird daher ihrem Zweck am angemessensten seyn,
wenn der Maaßstab des kleineren etwa 120 - 150 und der des
größeren 1000 - 1200 Ruthen umfaßt, und daher
die Entfernung des Höhenpunktes von E bei dem kleineren zu
5 - 6 und bei dem größeren zu 20 - 25
Ruthen nach dem Maaßstab 1:1250 angenommen wird.
- Wir haben also an dem eben beschriebenen Instrumente einen
Mechanism, durch welchen die Höhe des zu messenden Dreiecks mit
Leichtigkeit über einen angenommenen festen Punkt (B) der Kante
A D
gebracht wird, sobald diese A auf a an die Grundlinie
gelegt ist; wir haben ferner einen Mechanism durch welchen eben so leicht
aus dem Anfangspunkte dieser (nach E F
getragenen) Grundlinie eine Diagonale durch die, vermittelst des Triangels
J K L gefundene Höhe gebildet werden kann,
und haben endlich einen Maaßstab der so berechnet und eingerichtet ist,
daß uns die eben erwähnte Diagonale nach dem
§2 aufgestellten Satze,
den Inhalt der zu messenden Figur darauf abschneidet. Und dieß wars
was wir von dem Instrument begehrten.
Es ergiebt sich übrigens aus dem Allen von selbst, daß
das Instrument nach dem Maaßstabe des zu messenden Planes eingerichtet
seyn, und bei Plänen, welche nach einem andern Maaßstab aufgetragen
sind, auch ein anderer Flächenmaaßstab gebraucht, aber das gefundene
Maaß nach dem Maaßstabe des Planes reduzirt werden müsse.
- Die an den beiden Stäben O P und
P D angebrachte Eintheilung, dient zum Berechnen mit
Originalzahlen, wenn die Höhe der zu berechnenden Figur nicht über
5 und ihre Grundlinie nicht über 35 Ruthen beträgt.
Dieses Berechnen mit Originalzahlen ist, wenn es auch weniger fördert,
dennoch der Genauigkeit wegen bei ganz kleinen Grundstücken vorzuziehen.
Man erreicht zwar durch das planimetrische Messen besonders bei kleineren
Figuren eine größere Genauigkeit als durch Berechnen nach dem
Maaßstabe, diejenigen Fehler aber, welche aus Mangelhaftigkeit der
Werkzeuge durch das Auftragen und Ausziehen des Planes entstehen, können
nur durch Berechnung nach den Feldnoten ganz vermieden werden.
- Zur weiteren Erläuterung der von dem Instrumente
gegebenen Abbildung möge Folgendes dienen:
Vermittelst eines oben ausgebrochenen messingenen Schiebers,
welcher den Stab P D an der obern und den beiden
Seitenflächen umschließt, wird der Triangel
H F G an A D senkrecht fortbewegt
und vermittelst einer an e angebrachten gegen
P D drückenden Feder allezeit rechtwinkelicht
angezogen.
Dieses senkrechte Fortbewegen berüht hauptsächlich auf
der unter F G befestigten Leiste, welche bei F
senkrecht abgeschnitten seyn muß, damit der Endpunkt der Grundlinie einer
zu messenden Figur sich genau auf F übertrage, wenn der
äußere Rand der gedachten Leiste auf jenen gestellt ist. Der mit
f bezeichnete, auf beiden Seiten von e befestigte und an
dem abgeschrägten Rand des eingeschlossenen Stabes liegende Zapfen
verhindert beim Aufnehmen des Instrumentes das Abfallen des Triangels
H F G, welcher vermittelst einer an e
angebrachten, gegen den Stab P D drückenden Feder
allezeit rechtwinkelicht angezogen wird.
 Ein ähnlicher Schieber
(Fig. III) befindet sich auch an dem Triangel
I K L, nur daß diesem die innere Seitenleiste
fehlt indem hier der Triangel selbst an den Stab
O P anschließt und mit diesem horizontal auf dem
Papier aufliegt, da hingegen der Triangel H F G
über dem Lineal M N sich fortbewegt und daher um so
viel von dem Papiere absteht, als die Dicke des Lineals
M N und des Triangels I K L
zusammen beträgt. Der zwischen g und k befindliche
schmale Raum dient zur Erleichterung der 2ten Bewegung, bei der
3ten Aufgabe; so wie die auf b und g
angebrachte Eintheilung zum genaueren Ablesen der Schuhe und Zolle der darunter
befindlichen Maaßstäbe. Es versteht sich übrigens von selbst,
daß auf diesen wie auf dem Flächenmaaßstabe die angefangene
Eintheilung bis zu Ende fortgesetzt werden muß.
Ein ähnlicher Schieber
(Fig. III) befindet sich auch an dem Triangel
I K L, nur daß diesem die innere Seitenleiste
fehlt indem hier der Triangel selbst an den Stab
O P anschließt und mit diesem horizontal auf dem
Papier aufliegt, da hingegen der Triangel H F G
über dem Lineal M N sich fortbewegt und daher um so
viel von dem Papiere absteht, als die Dicke des Lineals
M N und des Triangels I K L
zusammen beträgt. Der zwischen g und k befindliche
schmale Raum dient zur Erleichterung der 2ten Bewegung, bei der
3ten Aufgabe; so wie die auf b und g
angebrachte Eintheilung zum genaueren Ablesen der Schuhe und Zolle der darunter
befindlichen Maaßstäbe. Es versteht sich übrigens von selbst,
daß auf diesen wie auf dem Flächenmaaßstabe die angefangene
Eintheilung bis zu Ende fortgesetzt werden muß.
Die beiden Ränder K L und
H F sind nicht senkrecht, sondern bilden mit der unteren
Fläche der Triangel einen Winkel von etwa 60°: bei dem ersteren damit
er das Licht besser zulasse und bei dem andern damit der Inhalt desto bequemer
abgelesen werden könne. Dies ist zugleich der Grund warum C
nicht senkrecht über der untern Kante von K L stehen
konnte und deswegen um so viel davon entfernt wurde als nachher die Punkte
E und F von A D.
- Dem bisher Gesagten, welches wie ich glaube, die
Einrichtung des Planimeters hinreichend erläutert und jeden geschickten
Mechaniker in den Stand setzen kann, durch Hülfe der beigefügten
Abbildung
dieses Instrument anzufertigen, will ich auch über den Gebrauch desselben
das Nöthige beifügen.

1te Aufgabe.
Den Flächeninhalt eines Dreiecks zu finden.
1) Man lege den Punkt A an dem Instrumente
dergestalt auf a (Fig. VI.)
daß die Kante A D an der Grundlinie
a b genau anliegt. 2) Man halte mit der rechten
Hand das Instrument fest und bringe mit der linken die Kante
K L bis auf c. 3) Man drücke mit der
linken das Instrument an und führe mit der Rechten das Lineal
M N bis an die Kante E. 4) Man setze
den Daumen der linken Hand auf das Lineal und bewege mit der rechten den
Flächenmaaßstab bis auf b, dann wird die innere Kante
des Lineals, den gesuchten Inhalt des Dreiecks
a b c an dem Maaßstabe abschneiden.
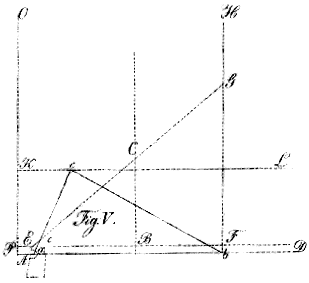 Die punktirten Linien (Fig. V.)
bezeichnen die Lage des Instruments über der Figur wenn alle 4 Bewegungen
gemacht sind:
E F - die mit
A D parallel auf das Instrument getragene Grundlinie;
C B - die, vermittelst
K L, über B senkrecht getragene
Höhe der Figur;
E G - die durch C gehende
Diagonale, welche in G den Inhalt der Figur an dem
Flächenmaaßstabe F H abschneidet.
Die punktirten Linien (Fig. V.)
bezeichnen die Lage des Instruments über der Figur wenn alle 4 Bewegungen
gemacht sind:
E F - die mit
A D parallel auf das Instrument getragene Grundlinie;
C B - die, vermittelst
K L, über B senkrecht getragene
Höhe der Figur;
E G - die durch C gehende
Diagonale, welche in G den Inhalt der Figur an dem
Flächenmaaßstabe F H abschneidet.
2te Aufgabe.
- Den Inhalt eines Parallelogramms zu finden.
Man denke sich
a b c d (Fig. VI.)
durch die Diagonale
b c in 2 gleiche Dreiecke getheilt und messe nun
eins derselben nach der 1ten Aufgabe, so ist das Doppelte
des gefundenen Maaßes der Inhalt der ganzen Figur.
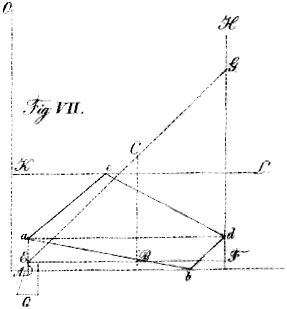
3te Aufgabe.
- Ein Trapez zu messen.
1) Man lege wie bei der 1ten Aufgabe
A auf a (Fig. VII.)
und A D
über a d; 2) Man drücke den Triangel
I K L mit der Linken fest an und ziehe mit
der Rechten das Instrument zurück bis die Kante
A D den Punkt b durchschneidet;
3) Man halte das Instrument mit der Rechten fest und schiebe
K L auf c; 4) Man bilde wie in den
vorigen Aufgaben eine Diagonale aus A und schiebe den
Maaßstab auf d, der alsdann da, wo ihn die innere
Kante des Lineals berührt, den Inhalt der beiden Dreiecke
a b c und
a d b zusammen angibt. Die Lage des Instruments
nach vollendeter Funktion ist hier ebenfalls durch punktirte Linien
angedeutet. Eben so bequem kann man bei diesen Aufgaben auch den Punkt
K und die Kante K L zum Anlegen
an die Grundlinie gebrauchen, und auf die vorgeschriebene Art verfahren.

4te Aufgabe.
- Ein Trapez gleich einem Parallelogramm zu messen,
wenn zwei Seiten desselben parallel sind.
Man halbire b c
(Fig. IX.)
in e und messe das Dreieck a e d
wie bei der 1ten Aufgabe gezeigt worden, dann verdoppele man
das gefundene Maaß so hat man den Inhalt des ganzen Vierecks: denn zieht
man g e f parallel a d
bis zum Durchschnittspunkt f der verlängerten Seite
a b, so entsteht das gleiche Parallelogramm
a f g d = 2 D a e d.
Bei Fig. VIII halbire man
a b und
c d, lasse aus e und f Senkrechte
auf a d fallen und verfahre dann mit
dem Dreieck g b h wie in der
vorigen Aufgabe gelehrt worden: denn
g h ist die halbe Summe der Parallelseiten
a d,
b c folglich Trap.
a b c d = 2 D g b h.
- Auch ein ganz unregelmäßiges Trapez
läßt sich in ein Parallelogramm verwandeln und auf dieselbe Weise
messen, es ist aber einleuchtend daß dieses Verfahren überhaupt nur
da mit Vortheil angewendet werden kann, wo man die dabei nöthige
Verwandlung der Figur ohne merklichen Irrthum nach dem Augenmaaß
bewerkstelligen kann, weil eine solche Construktion, wenn sie mit mathematischen
Werkzeugen vollzogen werden müßte, natürlich mehr Zeit
wegnehmen würde, als dadurch gespart wird, daß man anstatt 5
Bewegungen (wie bei Auflösung der 3ten Aufgabe) deren nur
4 zu machen hat, um den Inhalt der ganzen Figur zu finden. Erwägt man
nun noch, daß das hierbei erforderliche Verdoppeln des gefundenen
Maaßes schon leichter einen Irrthum zuläßt, und daß
dadurch auch die unvermeidlichen Fehler, welche Mangelhaftigkeit des Auges
oder des Werkzeugs hervorbringen, sich verdoppeln, so ist der Vortheil,
welchen dieses Verfahren gewährt nur sehr gering, und man thut in allen
Fällen, wo man nicht eine große Anzahl beinahe
regelmäßiger Figuren zu messen hat besser, sich des
§19 beschriebenen,
sicherern und genauern Verfahrens zu bedienen.
5te Aufgabe.
- Den Inhalt einer Figur zu messen deren Höhe
und Grundlinie durch Zahlen bestimmt ist.
1) Man richte den Triangel I K L
so, daß der Rand K R die gegebene Höhe
auf dem Maaßstabe P O abschneidet.
2) Man schiebe den Flächenmaaßstab an der Kante
A D fort bis der Rand F S
auf dem Maaßstabe A D die gegebene
Länge zeigt, so wird, wie bei den vorigen Aufgaben, das Produkt durch eine
aus E gebildete Diagonale abgeschnitten. Nur ist dabei zu bemerken,
daß man entweder zu dieser Berechnung einen besondern, für die
Eintheilung berechneten Flächenmaaßstab haben, oder daß
gefundene Produkt nach jener reduziren müsse, welches am leichtesten
dann geschehen kann, wenn die Eintheilung so gemacht ist, daß man nur mit
10 dividirt um die Reduktion zu vollziehen. Eben so leicht läßt
sich auch der Maaßstab so einrichten, daß beim Rechnen das
gefundene Produkt unverändert beibehalten, beim Messen dagegen mit 10
multiplizirt wird.
- In wiefern das Planimeter zugleich auch dazu dienen
kann, eine auf dem Papier aufgetragene Fläche in beliebige Stücke zu
theilen, wird demjenigen welcher überhaupt die Grundsätze solcher
Theilungen kennt, bald einleuchten. Obwohl indessen das Theilungsgeschäft
durch das Planimeter rascher von Statten geht als durch Rechnung, so
möchte doch die letztere Verfahrungsart der größeren
Genauigkeit wegen, in den meisten Fällen den Vorzug verdienen, und ich
habe es daher auch für überflüssig gehalten, diesen
Gebrauch des Instrumentes in der gegenwärtigen Abhandlung
umständlicher zu erörtern.
- Jetzt noch einige Worte über die Prüfung des
Instrumentes.
a) Man zeichne ein ungleichseitiges Dreieck und messe es wiederholt, indem
man eine Seite nach der andern als Grundlinie annimmt. Stimmen die Resultate
aller 3 Messungen überein, so kann man ziemlich versichert seyn,
daß in dem Mechanismus des Instrumentes kein Fehler obwaltet.
- b) Man theile eine als Grundlinie angenommene Länge
in 10 - 12 gleiche Theile, lege mit einer beliebigen Höhe das
Instrument darauf an, und messe nun zuerst den Inhalt der ganzen Figur, dann
setze man mit unverrücktem Instrument die Messung dergestalt fort,
daß man durch Fortschieben des Flächenmaaßstabes jedesmal von
der gemessenen Figur einen der eben erwähnten Theile der Grundlinie
abschneidet, so daß durch die letzte Messung der Inhalt eines einzelnen
Theils mit der angenommenen Höhe gefunden wird.
Nehmen nun alle einzelne Resultate in dem richtigen Verhältnis ab,
nämlich: n, n-1, n-2, n-3 ...
n-n, so ist dieß ein Beweis für die Richtigkeit
derjenigen Funktion des Instrumentes, durch welche die Grundlinie von dem
Papier auf das Instrument nach E F getragen wird.
Sind dagegen bei ganz richtigem Ansatz des Instrumentes die letzten (also
die kleinsten) Resultate im Verhältnis zu den ersten zu klein oder zu
groß, so wird in dem ersteren Falle die Grundlinie zu klein
und in dem andern zu groß nach E F
transportirt, welcher Fehler indessen entweder durch Berichtigung des
Anlegestrichs oder der, jedesmal die Grundlinie der Figur schließenden
Leiste unter dem Flächenmaaßstabe, leicht gehoben werden kann.
- Auf ähnliche Art läßt sich auch prüfen
ob der Punkt C die Höhe der zu messenden Figure genau auf das
Instrument überträgt, indem man nämlich auf eine
willkührlich angenommene Grundlinie eine Senkrechte errichtet, diese in
eine beliebige Anzahl gleicher Theile theilt und nun bloß durch
Fortschieben des Triangels I K L von einem Punkt zum
andern, die Höhe der Figur, aber nicht ihre Grundlinie verändert.
Die Vergleichung der durch diese Messungen gefundenen Resultate zeigt dann,
wie oben, ob die Höhe richtig auf das Instrument transportirt wird.
Ein vielleicht noch obwaltender Fehler der Art läßt sich
jedoch der Vor- oder Zurücksetzen des Punktes E
leicht heben, zumal wenn der Vorsprung E Q
so eingerichtet ist, daß er vor- und rückwärts geschraubt werden kann.
- Ob der Flächenmaaßstab des Instrumentes genau mit
dem des zu messenden Planes übereinstimme, läßt sich am
sichersten dadurch prüfen, daß man das Resultat einer mit
verschiedenen Grundlinien wiederholten Messung, einer genau konstruirten und
berechneten regelmäßigen Figur, mit dem der Berechnung im Mittel
vergleicht.
Wird der Flächenmaaßstab zu klein oder zu groß
gefunden, so hat der Fehler darin seinen Grund, daß eine von
C auf E F fallende Senkrechte
entweder zu wenig oder zu weit von E entfernt ist, und
es müßte also der eine oder der andere dieser Punkte beweglich
seyn, wenn das rechte Verhältniß gefunden werden sollte.
Da indessen ein diese Bewegung vollziehender Mechanism leicht der Genauigkeit des Instrumentes schaden könnte, so ist es
gerathener wenn der Mechanikus die Eintheilung des Flächenmaaßstabes
aussetzt, bis das Instrument fertig und in allen Bewegungen völlig justirt
ist. Dann ist es leicht nach dem Maaßstabe des zu berechnenden Plans eine
nach Gutdünken gewählte Höhe und Grundlinie auf das Instrument
zu tragen und vermittelst des Lineals M N
auf dem Flächenmaaßstabe einen Punkt zu bezeichnen der mit dem
Anfangspunkt des Maaßstabes (welcher durch E bestimmt wird)
das Maaß eines, aus der angenommenen Höhe und Grundlinie gebildeten
Dreiecks genau einschließt. Theilt man nun die gefundene
Länge nach dem aus den erwähten Faktoren durch Rechnung gefundenen
Produkte ein und setzt diese Eintheilung bis an das Ende des Maaßstabes
fort, so darf man bei sonst genauer Arbeit versichert seyn, das rechte
Verhältniß beider Maaßstäbe getroffen zu haben.
Diese hier vorgeschlagenen Prüfungen sind völlig
hinreichend um über die Genauigkeit des Instrumentes ein sicheres Urtheil
zu begründen und ich schließe daher hier meine Abhandlung mit dem
Wunsche daß das Planimeter durch den Gebrauch noch immer mehr
vervollkommnet und allgemein mit Nutzen angewendet werden möge.
Note:
Andries de Man
6/1/2001

 Ein ähnlicher Schieber
Ein ähnlicher Schieber

 Die punktirten Linien
Die punktirten Linien 
