
Outline Drawings of Calculator, showing correct
setting of arrows to scales.

BRITISH MADE THROUGHOUT


| (1) | THE HOLDER | } | on which are mounted spiral logarithmic scales. |
| (2) | THE CYLINDER | ||
| (3) | THE CURSOR (or Indicator), carrying at each end an engraved arrow, or pointer, which can be set to any mark, or to which any mark can be set. | ||
THE HOLDER carries a logarithmic scale 66 in. long, from 1 to 10, graduated as follows :—
| By | .001 | from | 1 | to | 1.12 | By | .005 | from | 2 | to | 4. | |
| ,, | .002 | ,, | 1.12 | ,, | 2 | ,, | .01 | ,, | 4 | ,, | 10. |
THE CYLINDER carries two scales in series which are identical in all respects with the above. The point at which, these two scales meet half-way up the Cylinder is denoted by the word "ONE," and is referred to in the following pages as the "MIDDLE UNITY," or "UNITY."
THE HOLDER SCALE on this Model is similar to the Holder Scale on Model K.
THE CYLINDER carries two scales, of which the upper one is identical with the Holder Scale, and operates with it for multiplication, division, &c. There being no MIDDLE UNITY on this scale, when calculations of this nature are performed on the Model L, the UNITY (one) at the top or bottom of the scale, as may be necessary, is used in its place.
The lower scale is graduated from 0 to 1, in 2,000 equal divisions of .0005 each. This is used in conjunction with the Holder Scale to give direct readings of the logarithm of any number, by means of which roots and powers are obtained.
The following sequence of movements should always be adhered to in operating the Instrument :—
| MOVEMENT 1. | Take the HOLDER in the left hand, and open Instrument gently to full extent. Move CURSOR to set bottom arrow. |
| MOVEMENT 2. | Move CYLINDER so that number on scale is set to top arrow (not the arrow to the number). Do not touch Cursor while moving Cylinder. |
| MOVEMENT 3.— | Move CURSOR to set either arrow as required — the companion arrow will then point to the answer (see following examples). |
GENERAL RULES.
The following abbreviations are used to render the descriptions more precise :—
| B = | Bottom Arrow or Pointer on Cursor. | ||
| T = | Top arrow or Pointer on Cursor. | ||
| Unity = | { | Middle Unity on Model K. Available Unity on Model L (see previous page). |
|
| To MULTIPLY. | To DIVIDE. | |
| 1. Set B to Multiplicand. | 1. Set B to Dividend. | |
| 2. Set UNITY to T. | 2. Set Divisor to T. | |
| 3. Move T to Multiplier. | 3. Move T to UNITY. | |
| 4. Read Answer at B. | ||
EXAMPLES.
The following instructions apply to both Models K and L.
|
|||
| Set B to 6. Set 7 to T. Move T to 4. | |||
|
|||
| Set 5 to T. Move T to 9. | |||
|
|||
| Set 2 to T. Move T to UNITY. Read answer at B: 3.086. |
| I. | Solve 12:7::16:x ? Set B to 12. Set 7 to T. Move B to 16. Read answer at T. 12:7::16:9.333. |
| II. | Solve 18:4::x:53 ? Set B to 18. Set 4 to T. Move T to 53. Read answer at B. 18:4::238.5:53. |
| III. | Divide 8975 in the proportions
83:79:33:19. Set B to 8975. Set sum of required proportions, viz., 214, to T. Without altering the setting of the Instrument, move T in succession to 83, 79, 33, 19, and read the corresponding proportions at B, viz., 3481, 3313, 1384 and 797. (On Model L this calculation necessitates "closing in" the Cylinder. See page 6.) |
 In Percentage Example I, for
instance, the Instrument being set to the constant terms 162: 100%, any
percentage of, off or on 162 will be shown at B when T is
moved to the relative figure, e.g., Move T to 45. Read answer at B:
45% of l62=72.9. Move T to 126. Read answer at B:
26% on 162=204.1, and so on.
In Percentage Example I, for
instance, the Instrument being set to the constant terms 162: 100%, any
percentage of, off or on 162 will be shown at B when T is
moved to the relative figure, e.g., Move T to 45. Read answer at B:
45% of l62=72.9. Move T to 126. Read answer at B:
26% on 162=204.1, and so on.
| II. | Decimalise 3/32, 7/32, 15/32,
29/32. Set B to 32. Set UNITY to T (32 and 1 being the constants in this series). Move B in succession to 3, 7, 15, 29 and read corresponding answers at T, viz., .09375, .21875, .46875, .9062. |
| To CLOSE CYLINDER IN. | Move T to bottom UNITY. Set top UNITY to T. |
| To OPEN CYLINDER OUT. | Move T to top UNITY. Set bottom UNITY to T. |
THE LOWER CYLINDER SCALE.— Where involved expressions occur above or below the line, the Otis King's Calculators offer valuable advantages over the ordinary slide rule, which, even if engraved with log-log scales, cannot solve the following, whereas Model L will give all powers and roots, fractional or otherwise, of all numbers without limit, and solve any expression, however extended. The following expression is given as an example :—
1.0083.1
x 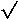 63 636 x 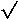 260000 260000 | = .2495 |
| 1.025
x 3.98
x 4000 6 x 12.11 x 900.1 |
To LOGARIZE —
(i.e., find the logarithm representing a number).
Set B to bottom UNITY of Holder Scale. Set
".000"
of lower Cylinder Scale to T. Move B to number (antilogarithm),
and read mantissa at T.
To DELOGARIZE —
(i.e., to find the number represented by a logarithm).
Set B to bottom UNITY of Holder Scale. Set
".000" of lower Cylinder Scale to T.
Move T to mantissa. Read antilogarithm (number) at B.
To ascertain any Power or Root of any number.
| POWERS. | ROOTS. | |
| Multiply the logarithm of the number by the index of the power and take the antilogarithm of the product. | Divide the logarithm of the number by the index of the root and take the antilogarithm of the quotient. | |
| Example :— What is
1.0083.1 Log. of 1.008=0.0035. 0.0035x3.1=0.01085. Antilog. of 0.01085=1.025. Therefore 1.0083.1=1.025. |
Example :— What is
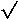 63 63Log. of 63=1.7993. 1.7993/3=0.5998. Antilog. of 0.5998=3.98. Therefore 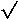 63=3.98 63=3.98 |
TO DETERMINE POSITION OF DECIMAL POINT.
| have | 5430000, +7 |
674, +3, |
81.2, +2, |
7.82, +1, |
0.45, +0, |
0.0421, –1, |
0.00675; –2 |
places |
| To find the number of places (p) in the product (P=XxY). | ||
| Let X have m places, and Y have n places. | ||
| RULE I. | p=m+n or p=m+n–1. | |
| (a) When the result is below the original setting p=m+n. | ||
| Example: 3x4 (m=1; n=1). Set B to 3. Set UNITY to T. Move T to 4 (This is below setting.) p=m+n=2. Answer=12. |
||
| (b) When the result is above the setting, the product has m+n–1 places | ||
| Example: 3x3 (m=1; n=1). Set B to 3. Set UNITY to T. Move T to 3. (This is above setting.) p=m+n–1=1. Answer=9. |
||
| To find the number of places (q) in the quotient (Q=X/Y). | ||
| RULE II. | q=m–n or q=m–n+1 as follows :— | |
| (c) When the result is above the setting, the quotient has m–n places. | ||
| Example: 3÷4 (m=1; n=1). Set B to 3. Set 4 to T. Move T to UNITY. (This is above setting.) q=m–n=0. Answer=0.75. |
||
| (d) When the result is below the setting, the quotient has m–n+1 places. | ||
| Example: 5÷4 (m=1; n=1). Set B to 5. Set 4 to T. Move T to UNITY. Read answer at B. (This is below setting.) q=1–1+1=+1. Answer=1.25. |
||
| RULE III. | Two methods may be used in working out complex problems involving both multiplication and division. They are :— | |
| (1) | Taking numerator and denominator alternately. | |
| (2) | Taking all the numerators first and then dividing consecutively by the denominators. |
| Example: | 432 x 32.4
x 0.0217 x 0.98 0.00000621 x 412000 x 0.175 x 4.71 |
=141.14... | |||||||
| No. | of | places | in | factors | of | numerator | =3+2+(–1)+0 | = +4. | |
| ,, | ,, | ,, | ,, | ,, | ,, | denominator | = –5+6+0+1 | = +2.
|
|
| Difference | = +2. | ||||||||
| Results of various steps in calculation | = –1+1+1 | = +1. |
|||||||
| Number of places in answer | = +3. | ||||||||
| Answer = 141.14. | |||||||||