Mathematisch-mechanisches Institut I. Schnöckel
Gegründet 1910. Berlin W. Steglitzer Straße 56. Gegründet 1910.

Spezialprospekt

über

Kompensationsplanimeter

mit Kugellager.

 

    Nr. 1. Kompensationsplanimeter mit Kugellager, D.R.G.M. und D.R.P. mit festem, etwa 30 cm langem Fahrstab, Teilung des Ablesemaßstabes in weißem Zelluloid plattiert, Konstantentabelle in Etui, mit 2 Präzisionsstahlkugeln, einer Lupe und Anleitung.

Preis bei portofreier Zusendung

Mark 25.-.  

 

    Nr. 2. Kompensationsplanimeter mit Kugellager, D.R.G.M. und D.R.P. mit verstellbarem Fahrstab, für 7 verschiedene Fahrstabeinstellungen justiert, die bequemen Multiplikationskonstanten in den gebräuchlichen Kartenmaßstäben entsprechen; Konstantentabelle im Etui, sonst wie bei Nr. 1.

Preis bei portofreier Zusendung

Mark 30.-.  
   
Planimeter Nr. 1 in Gebrauchsstellung mit Etui.
See below for explanation.

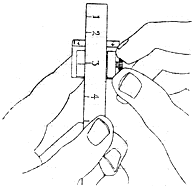
Verstellbarer Fahrstab des Planimeters Nr. 2.

 

Beschreibung des Instruments Nr. 2.

    Als Vorzüge können gelten:
    1.  Die freie Wahl der Multiplikationskonstanten bei bequemster Einstellung des Läufers am Fahrstab. (Vergl. obige Figur.)
    2.  Die Möglichkeit, den Papiereinschwand einer Karte (resp. deren Ausdehnung) zu berücksichtigen, indem man für je 0,1% Flächeneinschwand eine Läuferverschiebung von 0,2 mm eintreten läßt.
    3.  Die Erhöhung der Genauigkeit durch Fahrarmverkürzung besonders bei kleinen Flächen.

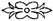
    Die neue "Anleitung für den praktischen Gebrauch der Kompensationsplanimeter mit Kugellager", deren Kenntnis hier vorausgesetzt wird, gilt in ihrem ganzen Umfange auch für die Ausführungsform Nr. 2. Diese unterscheidet sich von Nr. 1 dadurch, daß der Kugelanschlag nicht mit der Fahrstange unlösbar verbunden ist, sondern als Läufer an beliebiger Stelle durch eine Handbewegung fest angedreht wird. Er umschließt die Stange als ein U-förmiges Metallstück, das unten eine weiße Zelluloidplatte, den Kugelanschlag mit Indexstrich i zum Ablesen des Flächenmaßes trägt. Die
Maßtab der Karte
1:n		 Multi-
plikations-
konstante k
in qm		 Nr.
des Striches
auf der
Fahrstange
1:625 
1:625 
1:250 
1:500 
1:750 
1:1000
1:1000
1:1250
1:1500
1:2000
1:2000
1:2500
1:1250
     5
    8
    1
    5
  10
  20
  15
  30
  40
  80
  60
100
  20
 6
0
4
1
3
1
5
2
3
1
5
4
6
Abbildung zeigt den Läufer, dessen Index nach Bedarf auf einen der Teilstriche 0 bis 6 an der Fahrstange eingestellt wird. In nebenstehender Konstantentabelle ist in Spalte 3 auf diese Striche Bezug genommen.

    Hatte man im Kartenmaßstab 1:n  z.B. 1:1500 den Läufer auf Strich Nr. 3 gestellt und nach Umfahrung einer Fläche 2136 (die 6 geschätzt) abgelesen, so ist der Flächeninhalt das k=40 fache, also 85440 qm. Um auf der Fahrstange weitere Striche zu markieren, ermittele man den Abstand a des gesuchten Striches von Strich Nr. 1 nach der Formel:

a = 12,77 ( 20 - 10002
n2		 k ) Millimeter
wähle aber k so, daß a höchstens 10 cm lang wird.
    Man prüfe vor Beginn der Flächenberechnung die Tischplatte dadurch auf ihre Horizontalität, daß man die Kugel auswirft. Weicht sie in ihrem Laufe von der Geraden ab, so steht der Tisch schief, was zu beseitigen ist.
    In allen Fahrstabeinstellungen gilt die einfache Regel (Anleitung Seite 4), welche eine Probeumfahrung erübrigt, daß nach Aufstellung der Fahrstange der Läufer nicht in das Innere der Figur fallen und diese in der Richtung senkrecht zur Stange höchstens eine Handspanne (ca. 18 bis 20 cm) breit sein darf. Beachtet man dies nicht, so wird sich erstens nach der Umfahrung das Resultat oft nicht mehr ablesen lassen (über ca. 5 qdcm), dann aber auch nach der Planimetertheorie ein genaues Ergebnis überhaupt nicht mehr garantiert sein. Bei Umfahrung planimetrisch ungünstig geformter Flächen kann sich die hier wie beim Polarplanimeter nicht ganz zu tilgende, sogenannte Rollenschiefe, im Resultat - wenn auch nur wenig - bemerkbar machen. Sind die Genauigkeitsansprüche hoch, so eliminiert man diesen Fehler (Anleitung Seite 6) durch eine Kompensationsumfahrung in einer zur ersten etwa rechtwinkligen zweiten, die Fläche gleichfalls etwa halbierenden Fahrstangenlage, und bildet das Mittel aus beiden Resultaten. Bei den Umfahrungen erhalte man den Handgriff der Fahrplatte leicht drehbar.
    Es sei noch erwähnt, daß man bei der Flächenberechnung verzerrter Nivellements-Profile mit dem Längenmaßstab 1:n z.B. 1:1000 und dem Höhenmaßstab 1:m  z.B. 1:200 in obiger Formel für a die Größe n2 lediglich durch n*m ersetzen muß, sodaß z.B. für Strich Nr. 1 (also a=0) ist
k =   n*m  
50000		 .
    Die Kugel, welcher ein gewisser Rauhigkeitsgrad erteilt ist, schleife man nicht über das Papier, sondern lasse sie stets nur darüber hinrollen. Etwaiges Rosten derselben ist unschädlich.
    Bricht die Spitze des Ablesemaßstabes, so löse man deren Halteschraube, treibe den Stift durch einen Hammerschlag auf die Bruchstelle heraus und ersetze ihn aus dem "Vorrat".

Über 50 Planimeter mit
Kugellager wurden an die
Königlich Preussischen
Generalkommissionen geliefert.


Notes:
  1. Only one ball is used, the other is a spare part.   (back)
  2. Originally printed "5", hand-written "7".   (back)
  3. Unfortunately, I don't have this manual, but from an article in the Zeitschrift für Instrumentenkunde, June 1911, Vol. 31, p. 14, one can derive the following:
    • Put the cursor on the border of the area to be measured, in such a way that the area is not covered by the planimeter, and try to point the planimeter more or less towards the center of the area.
    • The ball should be at the special mark on the arm.
    • Put the measuring scale against the ball-stop, and read the scale at the index, try to get it close to zero.
    • Turn away the scale, by turning it around its pin, so it won't interfere with the arm while tracing the border.
    • Trace the border clockwise.
    • When the cursor is back at its starting point, turn the measuring scale against the ball-stop, and read the scale at the index mark. The difference between the two readings gives the surface area.
    • Apply a correction which has to do with the shape of the area, expressed as the ratio between the length of the area in the direction of the arm and the width of the area in the direction perpendicular to the arm. A table is provided for some rational values of this ratio.
    • Apply a correction which has to do with the distance between the final position of the ball and its starting mark on the arm. This distance is usually close to zero. A second table is given for this correction, with the distance varying between -0.75 and 0.75 mm. So what are we talking about....
      (back)
  4. Originally printed "1", hand-written "0".   (back)
  5. Originally printed "5", hand-written "6".   (back)
  6. Hand-written number.   (back)
  7. (Move the mouse over the descriptions below!)
  8. See also p.Galle, 130-131
  9. Picture of a Planimeter Nr. 2:

  10. In the Zeitschrift für Instrumentenkunde, June 1911, Vol. 31, p. 173, three versions of the planimeter are shown: one with two wheels, one with a ball, and one with a cylinder with extended edges. Note that in the drawing the measuring scale is pinned down by a large separate pin. In the marketed version, the scale has a splinter-size pin. c is a small stop that helps in putting the index at zero. In the marketed version this stop is not present. The picture also shows traditional tracing pins, instead of a see-through cursor.

    One of the big advantages of this planimeter is its cheapness: complete with case it costs 28 Mark, while a Coradi Polar Compensating Planimeter 2002, of about the same accuracy, costs 65 Mark ... in 1911.

 

Andries de Man 1/7/2000
1