PASCAL: AN INTRODUCTION

SETS
Sets exist in every day life. They are a way of classifying common types into groups. In Pascal, we think of sets as containing a range of limited values, from an initial value through to an ending value.

Consider the following set of integer values,

	1, 2, 3, 4, 5, 6, 7, 8, 9, 10

This is a set of numbers (integers) whose set value ranges from 1 to 10. To define this as a set type in Pascal, we would use the following syntax.


	program SetsOne( output );

	type  numberset = set of 1..10;

	var  mynumbers : numberset;

	begin
	end.

The statement

	type  numberset = set of 1..10;

declares a new type called numberset, which represents a set of integer values ranging from 1 as the lowest value, to 10 as the highest value. The value 1..10 means the numbers 1 to 10 inclusive. We call this the base set, that is, the set of values from which the set is taken.

The base set is a range of limited values. For example, we can have a set of char, but not a set of integers, because the set of integers has too many possible values, whereas the set of characters is very limited in possible values.

The statement

	var  mynumbers : numberset;

makes a working variable in our program called mynumbers, which is a set and can hold any value from the range defined in numberset.

SET OPERATIONS
The typical operations associated with sets are,

assign values to a set
determine if a value is in one or more sets
set addition (UNION)
set subtraction (DIFFERENCE)
set commonality (INTERSECTION)

Assigning Values to a set: UNION
Set union is essentially the addition of sets, which also includes the initialisation or assigning of values to a set.

Consider the following statement which assigns values to a set


	program SetsTWO( output );

	type  numberset = set of 1..10;

	var  mynumbers : numberset;

	begin
		mynumbers := [];
		mynumbers := [2..6]
	end.

The statement

		mynumbers := [];

assigns an empty set to mynumbers. The statement

		mynumbers := [2..6];

assigns a subset of values (integer 2 to 6 inclusive) from the range given for the set type numberset. Please note that assigning values outside the range of the set type from which mynumbers is derived will generate an error, thus the statement

		mynumbers := [6..32];

is illegal, because mynumbers is derived from the base type numberset, which is a set of integer values ranging from 1 to 10. Any values outside this range are considered illegal.

Determining if a value is in a set
Lets expand the above program example to demonstrate how we check to see if a value resides in a set. Consider the following program, which reads an integer from the keyboard and checks to see if its in the set.


	program SetsTHREE( input, output );

	type  numberset = set of 1..10;

	var  mynumbers : numberset;
	     value : integer;

	begin
		mynumbers := [2..6];
		value := 1;
		while( value <> 0 ) do
		begin
			writeln('Please enter an integer value, (0 to exit)');
			readln( value );		
			if value <> 0 then
			begin
				if value IN mynumbers then
					writeln('Its in the set')
				else
					writeln('Its not in the set')
			end
		end
	end.

More on set UNION, combining sets
Lets now look at combining some sets together. Consider the following program, which creates two sets, then joins the sets together to create another.


	program SetsUNION( input, output );

	type  numberset = set of 1..40;

	var  mynumbers, othernumbers, unionnumbers : numberset;
	     value : integer;

	begin
		mynumbers := [2..6];
		othernumbers := [4..10];
		unionnumbers := mynumbers + othernumbers + [14..20];
		value := 1;
		while( value <> 0 ) do
		begin
			writeln('Please enter an integer value, (0 to exit)');
			readln( value );		
			if value <> 0 then
			begin
				if value IN unionnumbers then
					writeln('Its in the set')
				else
					writeln('Its not in the set')
			end
		end
	end.

The statement

	var  mynumbers, othernumbers, unionnumbers : numberset;

declares three sets of type numberset.

The statement

		mynumbers := [2..6];

assigns a subset of values (integer 2 to 6 inclusive) from the range given for the set type numberset.

The statement

		othernumbers := [4..10];

assigns a subset of values (integer 4 to 10 inclusive) from the range given for the set type numberset.

The statement

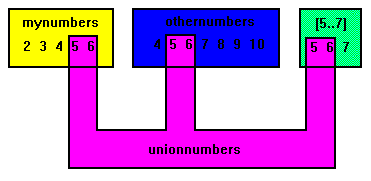
		unionnumbers := mynumbers + othernumbers + [14..20];

assigns the set of values in mynumbers, othernumbers and the set of values of 14 to 20 to unionnumbers.

If a specific value occurs in more than one set (as is the case of 4, 5, and 6, which are in mynumbers and othernumbers), then the other duplicate value is ignored (ie, only one instance of the value is copied to the new set.

This means that unionnumbers contains the values

Set Subtraction, DIFFERENCE
In this operation, the new set will contain the values of the first set that are NOT also in the second set.


	program SetsDIFFERENCE( input, output );

	type  numberset = set of 1..40;

	var  mynumbers, othernumbers, unionnumbers : numberset;
	     value : integer;

	begin
		mynumbers := [2..6];
		othernumbers := [4..10];
		unionnumbers := mynumbers - othernumbers;
		value := 1;
		while( value <> 0 ) do
		begin
			writeln('Please enter an integer value, (0 to exit)');
			readln( value );		
			if value <> 0 then
			begin
				if value IN unionnumbers then
					writeln('Its in the set')
				else
					writeln('Its not in the set')
			end
		end
	end.

unionnumbers contains the values

Set Commonality, INTERSECTION
In this operation, the new set will contain the values which are common (appear as members) of the specified sets.


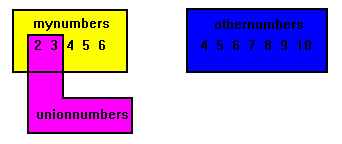
	program SetsINTERSECTION( input, output );

	type  numberset = set of 1..40;

	var  mynumbers, othernumbers, unionnumbers : numberset;
	     value : integer;

	begin
		mynumbers := [2..6];
		othernumbers := [4..10];
		unionnumbers := mynumbers * othernumbers * [5..7];
		value := 1;
		while( value <> 0 ) do
		begin
			writeln('Please enter an integer value, (0 to exit)');
			readln( value );		
			if value <> 0 then
			begin
				if value IN unionnumbers then
					writeln('Its in the set')
				else
					writeln('Its not in the set')
			end
		end
	end.

unionnumbers contains the values