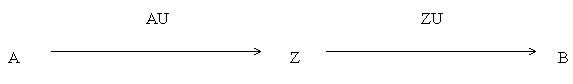
This text describes various aspects of cryptography, starting at the basics and building up to a good understanding of what can and cannot be done.
Feel free to link to this page or send comments, but refrain from copying this material.
All rights reserved by Jean-Philippe Martin.
The author can be reached at jpmartin@cyberjunkie.com.
Cryptography's initial goal was to protect information or messages so that only the intended recipient(s) could understand it (that is, to provide confidentiality). The technique used to "scramble" the message is called a code, or cipher. One of the early examples is the Roman cipher (called "Roman" because it has been used by Julius Caesar [CRY 71]) in which every letter in the message is replaced by the third letter that (circularly) follows it in the alphabet.
It must be noted that a message can be decrypted once an opponent understands how its work. At that point a completely different new code has to be elaborated. To prevent this, the concept of key has been invented: the key is a piece of information which is needed - on top of knowing which code is in use - to be able to decrypt the message. For example, the "offset" in the alphabet for the Roman cipher is a key: choosing the fourth letter ahead instead of the third would change the resulting message, so the key needs to be known in order to read the message.
One important property of this type of code is that both the sender and the recipient have to agree on which key they are going to use, and they have to keep that key secret. This is why this type of algorithm is called secret-key cryptography.
Naturally, secret-key cryptography is not limited to substituting letters for other letters: from changing the order of the letters to applying complex mathematical transformations, cryptography has evolved a lot. A good contemporary example would be triple-DES (DES stands for "Data Encryption Standard", it has been designed by IBM with the help of outside consultants and technical advise from the NSA (The U.S. "National Security Agency")(source NIS, pp. 42)): it uses a complex combination of substitutions and permutations (see [NIS 95], p. 42 for details) to achieve a very good level of security - as long as the secret key is shared between the two interlocutors only, i.e. kept secret.
And this, precisely, is the catch: the sender of the message must be able to send a secret key to the recipient, in a way that cannot be intercepted. If this can be done, why not simply exchange the messages that way? This is a serious limitation. In practice, it can be the case that the two party can meet physically to agree on the secret key and then use it for all further (possibly long-distance) communications; but what if the key gets compromised (that is, discovered by a third party) and a new key needs to be agreed upon?
Public-key cryptography, discovered in 1976 (1), makes it possible for two parties to communicate secretly without ever needing any secret channel.
To achieve this, two separate keys are used: the private key and the public key. The private key is kept secret while the public key is openly available. The public key can be used to encrypt a message, but then only the holder of the corresponding private key is able to decrypt the message. Two people can therefore communicate secretly by first exchanging their public keys and then using them to send messages to each other.
Public-key cryptography algorithms ensure that:
Here again, the knowledge of the algorithm being used does not help the attacker, since he still has to figure out what the private key is. Additionally, public-key cryptography (PKC) algorithms have to ensure that the private key cannot be deduced from the public key.
To achieve these goals, PKC algorithms use trapdoor one-way functions: these are functions that are much easier to compute in one way than in the other, except if some extra piece of information (the private key) is known. That is, a function f such that:
X = fk(Y) easy, if k and X are know
Y = fk-1(X) easy, if k and X are know
Y = fk-1(X) infeasible, if X is know but k is unknown
Unfortunately, this technique is not free of pitfalls either. Even though the public key does not need to be sent secretly to the receiving party, it is still necessary to know with certitude that the public key you have really corresponds to your partner's private key, or else you fall prey to the man in the middle attack.
Let's say that party A wants to send a message to B. We'll call A's public key AU and A's private key AR. {M}AU Will represent the message M, encrypted using A's public key. We shall call the "man in the middle" Z.
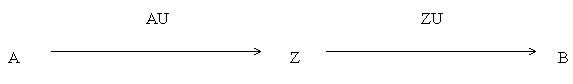
Thinking he has the correct public key, B now returns a message M to A:
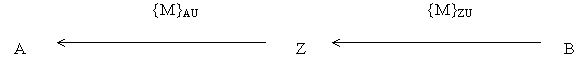
Z can decrypt the message using his private key since B unknowingly used Z's public key instead of A's. Z can then re-encrypt the message using A's public key so that A can still read the message.
This way, an attacker can read all the messages between B and A without them ever noticing anything (2))!
We have seen that secret-key cryptography allowed the secret exchange of messages, provided the parties share a secret key. Public-key cryptography (PKC) removes this constraint by using pairs of keys: a private and a public key. As a result, PKC does not require previous agreement on a common secret key to work.
An interesting fringe benefit of this system appears when every member of a group of individuals want to communicate secretly with one another. With secret-key cryptography all couple of parties need to agree on a secret key, making for n! keys in total. With PKC, however, the parties just need to know everyone else's public key, therefore only n key pairs are necessary in total.
Public-key cryptography's ability to use a different key for encryption and for decryption relies on the trapdoor one-way functions we have discussed in a precedent chapter. These functions' one-way facility relies on the fact that the function's inverse is NP-hard, that is the time to compute f-1 grows with the size of the key in a way that is faster than can be expressed with any polynomial. The functions whose computation takes a polynomial time are said to belong to NP.
However, the fact that no fast algorithm to compute f-1 has been found does not mean that there is none! Even though it is suspected there is no such algorithm (i.e. NP(NP-hard), it has not been proven yet. That's why secret-key cryptography builds on much more stable mathematical grounds than PKC.
Another drawback of PKC is that, in practical applications, it is much slower than secret-key cryptography. A common workaround is to use a mix of the two techniques: the program generates a random session key (a key that will be used only once), encrypts the document with secret-key cryptography using this key, and then adds this key, encrypted using PKC, to the file. This is used for example in the Pretty Good Privacy (PGP) software [PGP]. This way, encryption and decryption are fast while retaining the advantages of PKC. Additionally, this makes it possible to have a single encrypted file that can be decrypted by several recipients if it contains an encrypted version of the session key for each recipient.
For example, sending the message M to A and B using this technique would yield:
{M}S{S}AU{S}BU
Where S is the session key, AU is A's public key, and BU is B's public key.
Secret-key cryptography actually provides the only algorithm that has been proven to be impossible to break: the one-time pad. This algorithm requires a secret key that is at least as long as the text to send. Every bit of the text is then combined with a bit of the key (for example using the exclusive or function, "XOR") to form the encrypted text. The inverse manipulation is then done by the recipient to decrypt the message.
Even though this algorithm is proven to be unbreakable (3), it is rarely used! The reason for this is the complexity of sharing and distributing such a huge secret key (4). Also, should one want to store encrypted messages, that would require at least twice as much storage as an unencrypted version.
Digital signatures are (more or less) an electronic equivalent of a paper signature. They are the cornerstone of the digital certificates which will be further discussed in paragraph 2.4 'Public-Key Certificates' (see p. 2).
We have already seen that in PKC, documents encrypted with the help of the public key can only be decrypted with the private key. A very interesting feature of these algorithms is that it also works the other way round: a document encrypted with the use of a private key can only be decrypted using the matching public key. Or, to put it in another way: documents that can be decrypted with someone's public key can only have been encrypted with his private key.
This can be very useful when the sender of a message wants the recipient to know for sure that the message comes from him. When the sender sends a document encrypted using his private key, the recipient can know for sure (as long as he is confident that the sender's private key remains private) who the sender of the message is. This feature is called integrity because it makes sure no one can tamper with the message.
Since encrypting the whole message is a bit time-consuming and has the drawback of forcing the recipient to decrypt the message every time he wants to read it, a more efficient technique is used: before sending the message, the originator computes a "fingerprint" of the message, and he only encrypts this part (using his private key). This fingerprint must have the properties that it is easy to compute the fingerprint given a message but it is computationally infeasible to find another message that would match the fingerprint. The technique of hashing, which is described in the next paragraph, satisfies these requirements.
To summarize, for a party A to send a signed message m to B (using the hash function H), he needs to send the following information (where AR is A's private key):
m, {H(m)}AR
Anyone in possession of A's public key can check the signature, while everyone else can still read the message. Thanks to the properties of the hash function, only A can have generated this signature.
A hash function H generates a fixed-length output ("hash") from a variable-length message. Hash functions are used to produce a "fingerprint" of a document, that is a small piece of data that represents the document. It must have the following properties (adapted from a list in [NIS 95]):
1. H can be applied to a block of data of any size;
2. H produces fixed-length output;
3. It is relatively easy to compute for any given x, making both hardware and software implementations practical;
4. For any given code m, it is computationally infeasible to find x such that H(x) = m;
5. For any given block x, it is computationally infeasible to find y(x with H(y) = H(x), and
6. It is computationally infeasible to find any pair (x, y) such that H(x) = H(y).
The first three allow for practical implementations of a hash algorithm. The fourth property is a "one-way" property: it is easy to generate a hash code from a message but impossible to find a message matching the code. The fifth property is necessary to prevent forgery when an encrypted hash code is used (see also the paragraph 2.3.1 'Digital signatures').
A hash function satisfies only the first five of these properties is referred to as a weak hash function. If the sixth property is also satisfied, then the function is known as a strong hash function: these protect against the birthday attack, which we will discuss in the next paragraph.
This attack can defeat any weak hash function, for example a 64-bits hash. One could think such a hash is secure: an attacker would have to try, in average, 263 messages before finding one that generates the same hash.
There is however a different type of attack (5), proposed by Yuval [YUVA 79]. This attack can work when the attacker can, to a certain extent, choose the text that he will submit for signature. The attacker uses the following strategy:
1. The source, A, is prepared to "sign" a message by appending the appropriate m-bit weak hash and encrypting that hash with A's private key.
2. The opponent generates 2m/2 variations on the message, all of which convey essentially the same meaning. The opponent prepares an equal number of messages, all of which being variations on the fraudulent message to be substituted for the real one.
3. The two sets of messages are compared to find a pair of messages that produce the same hash code. The probability of success, by the birthday paradox, is greater than 0.5. If no match is found, additional valid and fraudulent messages are generated until a match is made.
4. The opponent offers the valid variation to A for signature. This signature can then be attached to the fraudulent variation for transmission to the intended recipient. Because the two variations have the same hash code, they will produce the same signature; the opponent is assured of success even though the encryption key is not known.
Thus, if a 64-bit hash code is used, the level of effort required is only on the order of 232.
Finding these 232 different texts is not even that hard: Space characters can for example be added or removed, or substituted for tabulation characters. Also, words can be replaced with synonyms (finding 32 such words is sufficient).
Authentication is defined by [CSS 94] as "the means of gaining confidence that people or things are who or what they claim to be". Authentication can be realized using either secret- or public-key cryptography, if one keeps in mind the possible attacks:
Replay attack: An attacker replays an earlier authentication message from a legitimate user to the same verifier.
Interception-and-replay attack: An intruder system is inserted in the path between the use and the verifier and actively modifies messages so that it looks like a legitimate verifier to the user and like an authentic user to the verifier.
Here is an example protocol where A would like to authenticate himself to B. A would send
A, n, {A, B, n}AR
Where n is a nonce, that is a number that will be used only once. To ensure this, we could imagine that n could be based on the time or that B would reject any nonce that it has seen already. In that last case, it is necessary to include B in the encrypted part of the message since B has no way to know whether the nonce n has already been used by another verifier C.
The nonce is needed to avoid replay attacks. Here, B can decrypt {A, B, n}AR using A's public key, making sure that the message really comes from A and that this is the first time this message is being received.
Non-repudiation prevents either sender or recipient from denying a transmitted message. Therefore, when a message is sent, the recipient can prove that the message was in fact sent by the alleged sender. Similarly, the sender can prove that the message was in fact received by the alleged recipient.
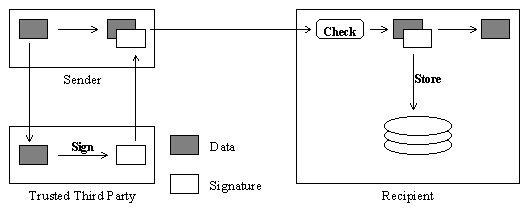
This task is usually split into non-repudiation of origin and non-repudiation of delivery. Non-repudiation of origin can be achieved, for example, by having the sender send his message to a trusted third party (TTP) who signs it (using PKC). Both the data and the signature are then sent to the recipient (who checks the signature before accepting the data). In this case, the trusted third party can be considered to be vouching for the sender. The benefit of using a TTP instead of letting the sender directly sign the message is that the sender may decide to "loose" its private key on purpose, therefore making the signature worthless.
This mechanism, illustrated in Figure 3, requires that the communication link between the sender and the TTP provides integrity and authentication so that the trusted third party can be sure it is signing a legitimate message.
Non-repudiation of delivery can be achieved by having the recipient send the data back to the sender and using non-repudiation of origin again.
Time-stamping consists in associating the current time to an electronic document in a way that is independent of the physical medium the data is stored in, and in such a way that it is impossible to change the data without that change being apparent. [TIME 97] defines a time-stamp of a document as something added to it as an evidence that the document has been issued before, after or at a certain time.
Time-stamps are needed for such purposes as confirming filing times of electronic business documents, for example.
One way to obtain time-stamps is with the help of a trusted third party: the sender can send a hash of the document to the TTP, who will append the current time and date and then sign the resulting data.
This algorithm is only sound as long as there is no risk of collusion between the sender and the TTP. This can be fixed by the use of the following linking protocol described in [TIME 97].
Suppose the sender A needs a time-stamp of its document, yn:
1. A sends IDn (his identity) and yn to the TTP.
2. The TTP sends back to A:
s = { n, tn, IDn, yn ; Ln }TR
where tn is the date and time, and TR the TTP's private key, and
Ln = (tn-1, IDn-1, yn-1, H(Ln-1))
where H is a hash function.
3. When the next request will be issued, the TTP will send IDn+1 to A.
(s, IDn-1) is the time-stamp for yn, and Ln is the linking information.
To verify the time-stamp, one must:
This way, even if a sender and the TTP collude, they cannot insert a fake time-stamp in the chain because the linking information is shared by all the people who submitted a document to time-stamp. To insert a fake time-stamp in the chain, the TTP and the sender would have to collude with the previous and the following person in the time-stamp chain. But even this can be detected during the verification by asking IDn+2 and IDn-2 for their time-stamps. In fact, one can check as many time-stamps as deemed necessary to trust the time-stamp's validity, up to the full length of the chain (6).
Steganography is defined by [NIS 95] as the techniques used to conceal the very existence of a message. It is only included here for completeness' sake, as the project is not related to these techniques at all.
A public-key certificates ties a public key (or other relevant information) to a person. This is typically done by using a unique string supposedly associated with an individual or other named object in the world. The bound is made by a Certification Authority ("CA") which is responsible for checking that the string is indeed unique and really identifies the individual whose public key is contained in the key.
How thoroughly this check has been made is described in a policy statement where the CA describes what assurance it can give that the name appearing on the certificate (called distinguished name, "DN") and the associated key really belong to the person named on this very certificate.
Once established by the CA, the link is put into concrete form by the CA signing the certificate. This way, neither the name nor the public-key on the certificate can be altered without the change being noticeable.
When a user trusts a CA, the CA's policy statement will tell him with which degree of certainty the certificates he receives bind the person to the key.
Figure 4 - certificate example
This definition of a certificate is quite general. Anyone could build his own home-grown certificate, like this one for example:
Assuming that you trust almostSign Corp and that the signature is correct, you would now know that the e-mail "jpmartin@cyberjunkie.com" belongs to the person called "Jean-Philippe Martin". almostSign's policy would tell you how this was tested.
Another aspect that is illustrated with this example is the use of validity dates on certificates. The rationale for this is that one may want to change the public key - remember that cracking a public key is never completely impossible, but just a matter of (usually extremely long) time. If certificates did not expire, people would have no way to distinguish between the new and the old ones (7). Worse, they could never know whether a new certificate exists and would hence continue using the old one forever.
Putting expiration dates on certificate ensures that the users will have to get a new certificate at some time. Thus, should someone decide to change his certificate, the users will get a more recent version at some point. Of course, this is no panacea but it helps to restrain the problem to a manageable size (8).
The ITU has defined a standard format for public-key certificates, called X.509. The X.509 standard relies on the X.500 directory (another standard from the ITU) to provide distinguished names.
Clearly, having one standard will help different programs understand various certificates. However, this standard is not very strictly defined. This results (for now) in incompatibilities between the various certificates. In this context, I would like to quote from [XSG 97], a short X.509 guide:
"In coming up with the worlds least efficient machine readable time encoding format, the ISO nevertheless decided to forgo the encoding of centuries. (...) Therefore, if the date is UTCTime and the year is less than or equal to 49 it's 20xx, if the date is UTCTime and the year is equal to or greater than 50 it's 19xx. (...)
To make this even more fun, another spec gives the cutover date as 2050/2051 rather than 2049/2050 (...)" - [XSG 97]
With the increasing use of certificates, however, there is good hope that these difficulties will be smoothed out soon.
Certificates are useful because they can help alleviate public-key cryptography's authentication problem and therefore reduce the risk for 'Man in the middle' attacks. They do not provide this by themselves, though: One still has to carefully choose who signs what and who trusts whom.
If there was one trusted third party everyone could trust, then the scheme would be simple: everyone would trust this TTP and get a certificate from it. This is of course not possible in real-life applications, be it only because the TTP may need to be close to the person who is applying for a certificate in order to perform the checks described in its policy. Besides, it would be an utopia to believe that one person or organization could be trusted by every single human being!
The system that is currently used in applications like Netscape Communicator uses a one-level hierarchy. Every user either trusts a given TTP or he does not; there is no "transitivity of trust". The system is nevertheless still useable for two reasons: (1) several TTP are trusted "by default" and (2) there are not that many different TTPs in the world yet. The day this situation changes, a need will arise for a more flexible trust system.
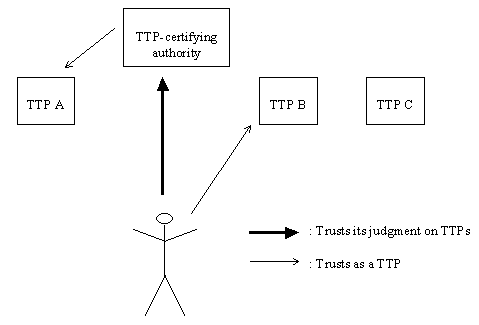
We have seen that it was necessary to have several TTP. This raises the question of how to choose the right one and, hence, the need for an authority (or several authorities) that checks the level of professionalism of the TTPs.
At this point we see the necessity for a new kind of trust relationship: the trust that someone can discern whether a TTP is trustworthy or not.
We end up with the schema shown in Figure 5.
Figure 5 - different trust relationships
In Figure 5, we see that the depicted user trusts TTP A and B, but not C. Of course, one can imagine that TTPs could double as TTP-certifying authorities.
Note that the trust as a TTP is only part of the relationship between a user and a TTP: the user still needs to know the TTP's policy statement in order to give a meaning to certificates signed by that TTP.
A good system would be to associate a policy statement with each of the arrows that leaves the user. That means that every TTP-certifying authority would provide a minimal policy statement that TTPs would need to follow in order to be accepted.
This way, the user could rely on a guaranteed minimal policy statement for all the TTP it trusts indirectly (for example, "all TTPs certified by the Swiss TTP-certifying authority check the link between full name and e-mail in a way that I trust") and know the exact policy of all the TTPs it would directly trust (for example "all certificates signed by the EPFL TTP contain a correct name, e-mail, address and phone number tied to the person's public key").
The two-levels hierarchy we have just seen is an efficient way to determine the trust level of a certificate in a environment where there are TTPs or maybe many TTPs, but what can we do in an environment where no TTP is organized, or where we do not feel we can trust any?
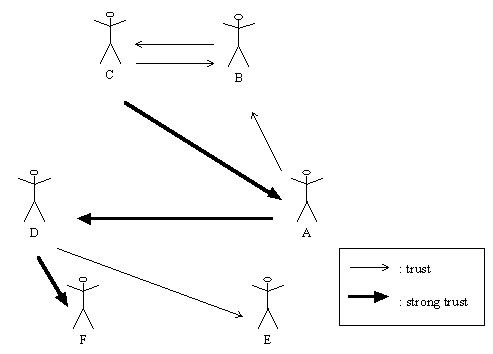
In such an environment we would need a more decentralized, "grassroots" approach. This is exactly what the "web of trust" provides. In this system, there are no TTPs but only users, with certificates. There are two trust relationships: The first is to trust that someone's certificate is valid and the second is to trust whether that person can judge whether other people only trust valid certificates.
The second type of trust, let's call it "strong trust", is very similar to the "trust judgment on TTPs" we have seen in the previous scheme. It means that we will trust the validity of all the certificates that the "strongly trusted" person trusts as valid.
The following is an illustration of the above:
Figure 6 - Web of trust
We can see here that user A trusts the certificates from the users B, D and E. Note that strong trust implies trust, since it makes no sense to trust in someone's judgment (based on his signature) if we are not even sure that the public key we have is his!
User C trusts certificates from users B, A and D, but not from user E nor F since C neither trusts E nor strongly trusts anyone who trusts E.
Note that in this system, there may be as many policy statements as there are users: users trust certificates that they are sure belong to the person they claim to belong to, and assign strong trust to users who they know apply a trust policy that is satisfying by their standards.
The web of trust is used almost as is in Pretty Good Privacy. It has the advantage of not needing any support infrastructure like TTPs. What's more, the user has full control over who he trusts and who he does not.
1 Public-key cryptography was first described in the open literature in a paper by Diffie and Hellman in 1976 [DIFF 76]. Yet the National Security Agency (NSA) claims to have discovered it some years earlier ([NIS]).
(back)
2 As long as Z can intercept all the messages between B and A, that is.
(back)
3 Which can be intuitively shown by the fact that a given ciphertext could be made to come from any cleartext by choosing a key that is ciphertext XOR cleartext.
(back)
4 This is a crucial problem, because as soon as a pad is reused the code is easily breakable. See [VENO] for an example of how the NSA, without the benefit of computer assistance, managed to decrypt a series of KGB messages encrypted with faulty pads.
(back)
5 The birthday attack derives its name from the "birthday paradox". This counter-intuitive result of probabilities shows for example that the probability for two people in a group of 23 to have the same birthday is greater than 0.5!
(back)
6 Further improvements are suggested in [TIME 97], which are out of the scope of this document.
(back)
7 The duration of the validity is subject to personal appreciation of the issuing authority.
(back)
8 Sometimes it may be necessary to issue a key revocation certificate when a key has been compromised. This raises interesting issues which are out of the scope of this document.
(back)
[CCS 94] Warwick Ford
[CLIB 97] Peter Gutmann [COR 97] Jean-Marc Geib, Christophe Gransart, Philippe Merle
[CRY 71] Laurence Dwight Smith
[DIFF 76] W. Diffie and M. Hellman
[NIS 95] William Stallings
[TIME 97] H. Massias and J.-J. Quisquater
[VENO] The National Security Agency
[XSG 97] Peter Gutmann [YUVA 79] G. Yuval
If you are looking for more information on this topic, check out Peter Gutmann's extensive Security and Encryption Links.
Links to more down-to-earth security-related pages are available at Computer Security Links (on this site).
I hope you enjoyed this document and maybe even found it useful. Please let me know what you think about it by sending me mail at jpmartin@cyberjunkie.com.
Putting It All Together
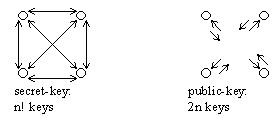
Other Uses for Cryptographic Techniques
Digital signatures
Hash functions
The birthday attack
Authentication
Non-repudiation
Time-stamping
Steganography
Public-Key Certificates
What a certificate is
-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA1
This e-mail: jpmartin@cyberjunkie.com
really belongs to this person: Jean-Philippe Martin
Certified by: almostSign Corp
Valid until: 1.1.2001
-----BEGIN PGP SIGNATURE-----
Version: PGPfreeware 5.0i for non-commercial use
Charset: noconv
iQA/AwUBNOgl0PiYJfhr9gz7EQJI7QCdG2U3ipKDxZq7w3Gjq96AIAh208EAn1zA
oJ1X8MIG9v9qIEO9DbD//hkf
=ViXW
-----END PGP SIGNATURE-----
Standards
The use of certificates
Two-levels trust hierarchy
Web of trust
Notes
Bibliography
Computer Communications Security
Prentice-Hall, Inc. 1994, ISBN 0-13-799453-2
Cryptlib encryption toolkit
http://www.cs.auckland.ac.nz/~pgut001/cryptlib/
CORBA, Des concepts à la pratique
Masson 1997, ISBN2-225-83046-0
Cryptography, the science of secret writing
Dover Publications 1971, ISBN 0-486-20247-X
New Directions in Cryptography
IEEE Transactions on Information Theory, November 1976
Network and Internetwork Security, principles and practice
IEEE Press 1995, ISBN 0-7803-1107-8[PGP] Philip Zimmerman, PGP Inc.
Pretty Good Privacy software
http://www.pgp.com
Digital timestamping and the evalutaion of security primitives
TIMESEC Technical report, March 1997
The VENONA Project
http://www.nsa.gov/docs/venona/venona.html
X.509 Style Guide
http://www.cs.auckland.ac.nz/~pgut001/pubs/x509guide.txt
How to Swindle Rabin
Cryptologia, July 1979