A quick tutorial by the Kevman.
Intro
A few posts on the LWML
lately were discussing animating cars and the like and how it can be done
in LW. Although Expressions can't answer everyones prayers, it can
be a quick solution for some things such as rotating the wheels of cars
moving along a road.
In this simple tutorial,
I'll explain how I worked out the solution to keeping wheels rolling in
perfect time with a car, even if you decide to speed up or slow down...
Well, to be exact, I'll show you how to roll one wheel - The other
3 or more will be simple duplicates of this one wheel! :)
The Process...
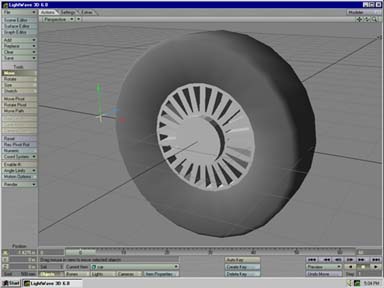 |
The first thing you will
need to do for this exercise is load in a model of a wheel, or a disc,
or whatever you plan to use.
In this example, I quickly modelled a wheel in modeler. Note that you will also need to know the size of your wheel too. My wheel was 2m wide - This means it has a radius of 1m... (Please note this as it is IMPORTANT) I also modelled the wheel on the Z axis so it faces the camera. This means that to roll the wheel, I will be changing its Bank angle. I suggest that you do the same, for the sake of making this tutorial simpler to follow. Load the model into Layout. Add in a Null object and call it 'car' - Then parent the wheel to the 'car'. Done that? Great, now we're ready to proceed! |
Before we start lets get some basic information to help us work out how we're going to calculate the wheel rotating. We know the following things about wheels:
- A complete rotation of a wheel is 360 degrees.
- A wheel travels the distance of its circumference in 360 degrees.
- If the circumference of the wheel is 2m, and a car moves forward 2m, therefore the wheel should rotate a full 360 degrees.
Usually I'll play with some numbers on paper to test my theories. Lets quickly make an example to test to prove this is correct:
Lets say for example, our circumference of the wheel is 2m.
The car moves 3m forward,
so that's 3m / 2m = 1.5 - So our wheel has to have rotated 1.5 times to
at 3m...
The car moves 12m forward,
so that's 12m / 2m = 6 - Our wheel rotates 6 times at 12m...
We know that a complete rotation is 360 degrees, so therefore we can work out that the rotation of a wheel at a given time will be:
(Current distance of car / Circumference of wheel) * 360 degrees
Thats the expression we need!
This exercise will be very quick and easy - Simply click on the Graph editor,
then select the wheel object and select the wheel.Rotation.B channel.
From the Modifiers,
Add modifier / LW_Expressions. Then, double-click
on the LW_Expressions modifier to bring up its settings.
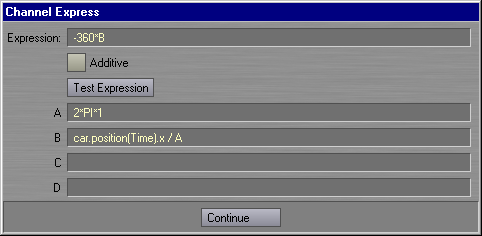 |
Like my previous tutorial,
I've split the calculations out over the A-D variables to make them easier
to follow.
In A, I've calculated the circumference of the wheel. The equation for the circumference is: 2 * PI * Radius of wheel (In my example, I know that the radius is 1m) I then calculate the distance
of the car divided by the circumference(A) in B. My
car will be driving on the X axis, so I get the cars position at the current
time with the expression command car.position(Time).x
|
Finally, I calculate the wheels rotation in the Expression line. -360 * B - I used a negative number because using a positive number rotated the wheel in reverse! Feel free to change -360 to 360 and see for yourself!
To test that this is working, move the 'car' null back 1m and keyframe it at 0. Move the 'car' forward 1m and keyframe at 60. You need to create keyframes, because the expression asks for the position of the 'car' at a certain 'Time' (ie. frame). Just dragging the null back and forwards will have no effect on the preview window, so don't be fooled that it isn't working straight away...
Then play and you should see the wheel rotating in perfect precision!
That's it!
Please note that this expression will only work if the car is moving in a straight line. Its not designed to compensate for turning, reversing, and dropping wheelies!
Also, with some simple alteration of the way this calculation works, you can move the car based on the rotation of the wheel instead! Ideal for animating objects moving along a conveyor belt perhaps? Or you can drag race that hot rod by simply controlling the speed of the wheel rotation! But I'll leave that as an exercise for you to work out - hint - Similiar formula, just reorder it a little! ;)
I hope that this has been
eductional for some of you out there!
Kevin 'kevman' Phillips
This page/article Copyright© 2000 Kevin Phillips