The amount of loss incorporated in compressing and decompressing image frames using a lossy compression algorithm is related to the nature of the algorithm as well as the accuracy with which the numerical operations are carried out during the process (Clarke 85). Variations in pixel values may even cause degradation and distortion in the image frames. Due to the nature of the JPEG image compression algorithm (Wallace 90), blocks of an image with large amounts of high frequency information generally suffer more degradation than the blocks containing lower amounts. Moreover, such defects increase with higher compression ratios.

Efficiency of an image compression algorithm may be judged from the quality of a reconstructed image with respect to the original reference image in relation to the compression ratio. This is usually accomplished by performing subjective analysis of the reconstructed images. Human observers are employed to conduct the subjective assessment of image quality (Kostic 83). It is generally dependent upon a number of factors such as the viewing conditions, perception of the viewers as well as the nature of the images used (Hanson 87). Accurate subjective analysis may, therefore, only be carried out using significantly large number of observers who have to be selected randomly.

The relative expensive of subjective evaluations, therefore, forces organisations involved in development of video and image processing systems to develop and employ objective measures of image quality assessment. The measures used must be able to provide reliable and consistent results. Two such algorithms are discussed here. The first algorithm, known as the Minimum Distance Algorithm for Image Similarity, is based on the Minimum Distance Classification of pattern recognition. The second algorithm is logical in nature. It is known as the Significant Difference Density Algorithm.

Root mean square error (RMSE) between the original image and its reconstructed copy is the most commonly used image quality measure. This may provide a very broad indication of the quality of the reconstructed image, which may not be an accurate indicator (Parson et al 75). If some degradation is evenly distributed over the whole image, the RMSE between the original and reconstructed images may fall below the threshold. Lossy image compression and decompression algorithms also alter data in a manner so as to cause objectionable image defects in certain areas of the image, e.g., changes in the sharpness or location of edges, changes in contrast across the boundaries (Russ 95).

Due to the nature of compression algorithms based on transform coding, e.g. JPEG image compression algorithm, reconstructed image frames may suffer distortion or degradation within blocks of images (Rayner 91). An image with such visible degradation may pass the RMS error check but will not be appreciated in the subjective analysis for determining the image quality (Sonka et al 93).

An obvious approach in determining the quality of images compressed and decompressed using the transform coding methods is to perform analysis operations on the respective blocks of original and reconstructed images. These block by block analysis are based on determining significant similarities between respective blocks of the original and reconstructed images. Measures thus adopted should be able to indicate blocks in the reconstructed image that are sufficiently dissimilar to their counterparts in the original image. These blocks should contain visible dissimilarities from their counterparts in the original image or should appear discontinuous in the reconstructed image.

Similarity is taken as being different from same. Same data in two images means exactly same numerical values within the maximum allowable resolution. Data within two images may not be same but may still be regarded as similar if it does not create significant or visible changes in luminance, edges, boundaries, colour composition etc.

Minimum Distance Algorithm for Image Similarity Assessment

This algorithm is an adaptation of the Minimum Distance Pattern Classification principle. Pattern classification by the distance function is one of the earliest concepts in automatic pattern recognition. Minimum distance classification is an effective approach to classify patterns if the patterns of each class tend to cluster tightly about a typical or representative pattern of each class (Gonzalez et al 74).

Consider M pattern classes and assume that these classes can be represented by prototype patterns z₁, z₂, z₃, … z_n. The Euclidean distance between an arbitrary pattern vector x and the i^th prototype is given by equation 1.

[1]

A minimum distance classifier computes the distance from a pattern x of unknown classification to the prototype of each class and assigns the pattern to the class to which it is the closest (Gonzalez et al 1974).

In the Minimum Distance Algorithm for Image Similarity Assessment, the original colour image block of 8×8 pixels is considered as one representative pattern. The most distorted image patch, possible for the original image under consideration, is then computed. This is accomplished by assigning zero to an array element for which the corresponding array element in the original image block is greater than or equal to 128. All other array elements are assigned the values of 255. For example, consider the following image patch,

the most distorted image patch possible for this image is as follows

The Euclidean distance between the original and the most distant or distorted image patches is computed as follows,

[2]

where

x_ij : amplitude of arbitrary input element

xd_ij : amplitude of the most distant counterpart of x_ij

 d_max : distance between the input image block and the most distant image block

Euclidean distance between the original and the reconstructed image patches is then calculated by a similar expression given in equation 3

[3]

where

x_ij : amplitude of arbitrary input element

x’_ij : amplitude of the reconstructed counterpart of x_ij

 d : distance between the input image block and its reconstructed counterpart

The similarity factor, S, between the blocks of the reference and the reconstructed image blocks is then computed using equation 4.

[4]

Higher the value of S, greater is the similarity between the original and reconstructed image blocks.

The Significant Differences Density Algorithm

This algorithm determines the density of significant differences between the original and reconstructed image blocks. Higher the density of significant differences, more is the likelihood of the distortion or dissimilarities between the original and reconstructed image blocks. This is relatively a computationally inexpensive algorithm which, at the time of writing, had been developed and tested only to a proof of concept stage. The algorithm may need to be enhanced to improve its accuracy in indicating dissimilarities between the image blocks.

As a first step, the original image (O) is subtracted from the reconstructed image (R) pixel for pixel. The difference image (D) is then converted into a binary image (B). If the absolute value of any pixel in difference image is greater than a certain threshold (T), e.g. 20, 1 is assigned to the corresponding pixel in the binary image. Alternatively, if the absolute value of a pixel is less than the threshold, a 0 is assigned to the corresponding pixel of the binary image. These steps have been summarised in [5] and [6].

[5]

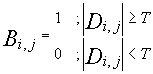  [6]

 where 0 £i<Max Image Length and 0 £j<Max ImageWidth

The density of significant differences in the 4 quadrants of each 8×8 block of the binary image is calculated. This is accomplished by adding all the 1’s in a quadrant and dividing them by 16. If this value for any quadrant is greater than a certain pre-defined threshold, e.g. 0.4, no further tests are conducted and the reconstructed image block is tagged as being dissimilar from the corresponding reference image block.

It is possible that the distortion is distributed between two or more quadrants of the image block (Figure – 1). In this case, the density of significant differences in each quadrant may be well below the specified threshold but the block contains a visible distortion. Thus, if the density of significant differences is not greater than the threshold in any of the quadrants, the density of significant differences in the entire binary image block is calculated. Here, if the density of the significant differences is greater than a specified threshold, the reconstructed image block is tagged as being dissimilar from the reference image block.

Figure – 1 : Distortion Distributed in the Quadrants of an 8×8 Image Block

If the image block passes this test as well, it is subjected to a tougher quality check using the Quality Operator (Figure – 2). The Quality Operator is a 3×3 matrix, which is moved within the image block to determine the significantly different pixels that are adjacent to one another. It is possible that the density of significant differences within an image block or any of its quadrants is below the specified threshold, but the pixels with significant differences are adjacent to one another, thus causing a visible distortion.

Figure – 2 : Quality Operator

The Quality Operator is first moved horizontally within the binary image block at all the possible locations. The Quality Factor, Q, is the sum of the values of all the elements of the binary image that fall under the quality operator,

 [7]

where i, j are the indices of the Quality Operator, with the central element being the reference.

If the value of Q is greater than 3 then it means that 4 or more pixels out of nine are significantly different at that location. The block is then tagged as having a visible distortion or degradation. If the value of Q is equal to 3, the algorithm checks if such an event occurred in the previous location of the Quality Operator. The occurrence of such an event in the previous location of the Quality Operator also suggests the presence of significant differences that may amount to visible distortion.

If no distortion or degradation is detected in the horizontal scan of the Quality Operator on the binary image block, the Quality Operator is scanned vertically over the binary image block. The conditions indicating a significant dissimilarity during the horizontal scan of the Quality Operator also apply to its vertical scan.

Each pixel in a colour image is represented by 3 integer values, one for red, one for green and one for blue. Thus an 8×8 colour image block is represented by a 24×8 matrix of integer numbers. In this case, the binary image derived from the difference image is also a matrix of 24×8 integer values. The value of each element of this matrix represents the state of a specific colour element of a pixel (i.e. colour component of that pixel in the reconstructed image block being significantly different from the same colour component for the corresponding pixel in the original image block). This matrix of 24×8 integers can actually be collapsed into a matrix of 8×8 integer numbers by taking a logical OR of the binary value for each colour component of the respective pixels. Each element of this collapsed matrix represents whether that particular pixel in the reconstructed image block is significantly different from its counterpart in the original reference image block.

Potential Applications

Subjective measures of image quality assessment are generally used to ascertain the quality of the image processing equipment. These measures, however, involve a significant operational cost for the organisation. Initial development costs of reliable objective measures of image quality assessment may be high, but the operational costs (both tangible and intangible) are definitely lower than that of subjective analysis. Thus significant amount of research and development activity is contributing towards the development of effective and reliable objective or quantitative measures of image quality analysis.

The measures thus developed have been used for testing image processing equipment and diagnosing faults at the required level. The actual techniques used in a particular system however depend upon the processing carried out within the device under test as well as the diagnostic resolution required by the user. Examples of such test systems include those developed by Voran et al (1992) and Lourens (1991). The algorithms discussed here can be used to functionally test JPEG encoders and decoders.

Parson et al (1975) have demonstrated the application of RMS error analysis in optimisation of image compression algorithms. Measures described above may also be used in an operational environment, where the results furnished by them may be used to automatically vary the compression ratios to achieve the desired image quality. Successful development of such a system may solely depend on an optimal hardware implementation of these measures.

Conclusions

The two algorithms discussed above, i.e., the Minimum Distance Algorithm for Image Similarity Assessment and the Significant Differences Density Algorithm, were developed to counter the drawbacks inherent in the standard statistical measures which restrict their application to image quality measurements. Both these algorithms have certain strengths and weaknesses, which must be understood and taken into account before using them in any application.

The main feature of the Significant Differences Density Algorithm is its logical nature. It works on a set of conditions and when any one of these conditions is true, the block being compared is tagged as dissimilar. A number of variations of this algorithm are possible. For example, if the density of significant differences is below a specified threshold, the path of significant differences is traced. If the path is longer than a certain threshold, it may be regarded as a visible distortion in the reference image frame.

At the present state, this algorithm cannot provide a degree of dissimilarity between the original reference and the reconstructed image blocks. It can be modified to provide the density of significant differences at various locations, or the length of the longest chain of significant differences. Moreover, the selection of all the thresholds in the algorithm require a substantial number of experiments to be carried out on different images with varying degrees of dissimilarities between the reference and the reconstructed image frames.

The Minimum Distance Algorithm for Image Similarity Assessment provides a numerical figure for similarity between the original reference and the reconstructed images relative to the maximum possible distortion. 100 means that the data within the reference and the reconstructed image blocks is numerically the same. Higher the value of this figure, more is the similarity between the two image blocks. Only one threshold, i.e. the percentage similarity between the tolerable and intolerable dissimilarities requires adjustment. Moreover the algorithm takes into account, not only the significant differences, but also the insignificant differences between the reference and reconstructed image blocks. Under certain circumstances, a significant number of insignificant differences may cause appreciable error in images. The Significant Differences Density Algorithm may not be able to detect these errors at its present level of development. An adaptive version of this algorithm may, however, be able to detect and identify a wider range of image defects.

Clarke R.J. (1985), Transform Coding of Images, Academic Press Inc. (London) Ltd.

Gonzalez R.C. & Tou J.C. (1974), Pattern Recognition Principles, Addison Wesley Publishing Co.

Hanson J. (1987), Understanding Video, Applications, Impact and Theory, Sage Publications Inc.

Kostic B. (1983), Analogue and Digital Video Signal Processing Using a Scrambling Strategy, PhD Thesis, Loughborough University of Technology.

Lourens J.G. (1991), Objective Image Impairment Detection Using Image Processing, 4^th International Conference on Television Measurements, 20 – 21 June 1991, pp 13 – 19.

Parson J.R. & Tescher A.G. (1975), An Investigation of MSE Contributions in Transform Image Coding Schemes, in Efficient Transmission of Pictorial Information, Proceedings of the Society of Photo-optical Instrumentation Engineers, August 21-22, 1975, San Diego, USA.

Rayner A. (1991), Evolving Error Performance Parameters & Objectives for the Digital Transmission of Broadcast Television, 4^th International Conference on Television Measurements, 20-21 June 1991, pp 114-120.

Russ J.C. (1995), The Image Processing Handbook, CRC Press Inc.

Sonka M., Hlavac V. & Boyle R. (1993), Image Processing, Analysis and Machine Vision, Chapman & Hall.

Voran S.D. & Wolf S. (1992), The Development and Evaluation of an Objective Video Quality Assessment System that Emulates Human Viewing Panels, International Broadcasting Convention, Amsterdam, July 1992, pp 504 – 508.

Wallace G.K. (1990), Overview of the JPEG (ISO/CCITT) Still Image Compression Standard, SPIE Image Processing Algorithms and Techniques, 1990, 12244, pp 220-233.

Ballard D.H. & Brown C.M. (1982), Computer Vision, Addison Wesley Publishing.

Barnsley M.F. & Hurd L.P. (1993), Fractal Image Compression, A.K. Peters.

Boyle R.D. & Thomas R.C. (1988), Computer Vision, A First Course, Blackwell Scientific Publications.

Duda R.D. & Hart P.E. (1973), Pattern Classification and Scene Analysis, John Wiley & Sons Inc.

Gonzalez R.C. & Woods R.E. (1992), Digital Image Processing, Addison Wesley Publishing Co.

Inglis A.F. (1993), Video Engineering, McGraw Hill Inc.

Nadlar M. & Eric P.S. (1993), Pattern Recognition Engineering, John Wiley & Sons Inc.

Noll A.M. (1988), Television Technology, Fundamentals and Future Prospects, Artech House Inc.

Pearson D.E. (1975), Transmission and Display of Pictorial Information, Pentech Press, London.

Schalkoff R.J. (1989), Digital Image Processing & Computer Vision, John Wiley & Sons Inc.