Independencia 02: Variables
En la simulación anterior, para jugar el "cuatro en línea", programé dos sensores (tamaño del tablero y saber si había una celda ocupada) y una acción (colocar un símbolo en una celda). Los algoritmos generados manejaban solo cuatro variables: w, x, y, z. Como programador se que son muy pocas ¿entonces cuantas variables deben haber?.
La respuesta esta en la propia naturaleza de sensores y acciones. Cada sensor envía una serie de datos al organismo, cada dato es entonces una variable de lectura, una acción en cambio es enviada por el organismo, luego son variables de escritura.
Con esto en mente se optimiza la generación de organismos:
Variable_Accion = Funcion (Variable_Sensor);
IF ( Variable_Sensor >,<,=,<> Condicion (otras variables de sensor) ) THEN
El hecho es generar en forma aleatoria pero con mayor probabilidad de éxito los organismos jugadores. Se mantiene la independencia del algoritmo evolutivo.
| x | x | x | ||||||||
| x | ||||||||||
| x | x | |||||||||
| x | x | x | ||||||||
|
|
||||||||||
| x | x | x | ||||||||
| x | ||||||||||
| x | x | |||||||||
| x |
Para esta simulación se crean dos sensores y una acción:
1. Sensor de tamaño del tablero: devuelve en cuatro variables las coordenadas de la celda inicial (0,0) y las coordenadas de la celda final (10, 10).
2. Sensor de ocupación de celda: El organismo envía dos variables de acción (coordenadas de celda) y el sensor retorna si esta esta ocupada (tiene X) o vacía.
3. Acción (llenado de celda): El organismo envía otras dos variables de acción (coordenadas de celda) y la acción llena la celda; retorna si hubo éxito o no de esta acción.
Tendremos al final, 6 variables de sensor y 4 variables de acción.
Un algoritmo aleatorio se vería así:
Casillas Llenas: [7]
function Organismo.fSerVivo(Sensores: real, Acciones: real):real;
begin
1: F:1;
2: A4 := S1+S1-S1-S1*7+S1/S1;
3: F:2;
4: A4 := ((S2-S2/S2+S2-S2+S2));
5: A1 := 7*9+((S2-S2/((4)+3)));
6: A1 := S6/S6+4-(S6-4-2);
7: F:2;
8: F:3;
9: if S2 < S3-3/S3+S3-S3*S3/S3 then Goto 38;
10: A3 := 2+S6/((S6)*6)+S6;
11: if S2 > (S1+S1/1/9/S1+7) then Goto 40;
12: F:3;
13: F:3;
14: F:1;
15: if S6 < S2/S2/S2*S2*S2+S2/S2 then Goto 14;
16: F:1;
17: if S3 < (9-5-S4/S4/S4-S4) then Goto 34;
18: A1 := 2*(9-S6*(7+S6+1));
19: A3 := S5-3/1+5/(5-4);
20: A4 := 6-S5/S5+S5*((S5*4));
21: F:3;
22: A3 := (S4)-5*S4*(S4*S4);
23: if S2 > S3/((S3)+((2+S3))) then Goto 5;
24: F:3;
25: A1 := S4+S4-(8+S4-3/S4);
26: if S2 < 1-(((S4+(2+S4*4)))) then Goto 15;
27: F:3;
28: F:1;
29: A2 := 2*S1/S1/S1*(S1-3);
30: A1 := (5+7)-(S5-6/S5);
31: A4 := 5*S6+(S6+7*S6/S6);
32: A3 := S3*(S3+S3*S3)/S3+S3;
33: A4 := 4-S5+6*S5-S5+S5-S5;
34: if S1 < S6*S6/2*S6+8-S6+1 then Goto 1;
35: A3 := 4-(S6/S6-S6)+7/5;
36: A3 := 5-S4-(7*S4-S4/S4);
37: F:1;
38: F:1;
39: A2 := S5-5/S5*S5+(S5-1);
40: A2 := S2*7*(S2+8-S2+S2);
end;
Las variables A1, A2, A3 y A4 son variables de acción.
Las variables S1, S2, S3, S4, S5, S6 son variables de sensor.
F:1, F:2, F:3 son las funciones.
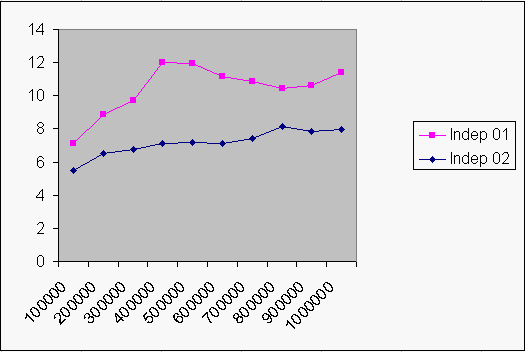
Los resultados de esta segunda simulación son algo desalentadores, son menos exitosos que la simulación anterior en el cual teníamos tan solo cuatro variables. Esto puede entenderse a simple vista: hay 6 variables de sensor y 4 variables de acción (10 variables en total), luego el número de combinaciones es inmensamente mas alto que el uso de solo cuatro (a pesar de que este último es una mezcla sin sentido de valores).
Observe el gráfico en que confronto la simulación anterior (independencia 01) con esta nueva (mas alto es mejor). Desde 100 mil a 1 millón de algoritmos generados.
