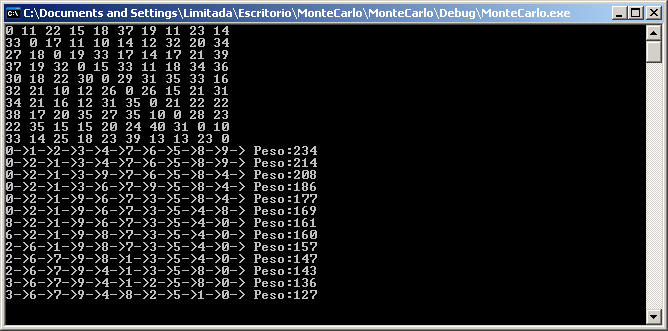
Método de Monte Carlo. Problema del viajero
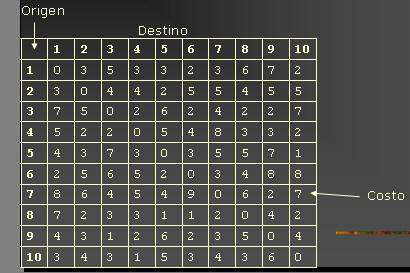
Uno de los problemas difíciles de resolver es el problema del viajero: Dado un número N de ciudades a recorrer, ¿cual es el camino con el menor costo dada la tabla que se ve a continuación?:
En la imagen se observa un tablero de costos, en el que señala cual es el costo de ir de una ciudad a otra, por ejemplo ir de la ciudad 2 a la ciudad 7 cuesta $5. Por supuesto si la ciudad destino y origen son las mismas, no hay tal viaje por lo que cuesta $0. Algunos se preguntaran porque ir de A a B cuesta diferente que ir de B a A, la respuesta es sencilla: Si el viento sopla de Oriente a Occidente y usted tiene un velero, cuesta muy poco viajar de Oriente a Occidente, pero si es la ruta contraria tendrá que recoger las velas y usar motor, un costo mucho mayor.

El objetivo es pasearse por todas las ciudades minimizando el costo, pero es un problema en el que hay que probar N! (N factorial) posibles soluciones para buscar la ruta de menor costo (un número muy grande) que aumenta enormemente por cada ciudad adicionada.
La solución utilizando Método Monte Carlo es:
1. Genere una ruta inicial y evalúela
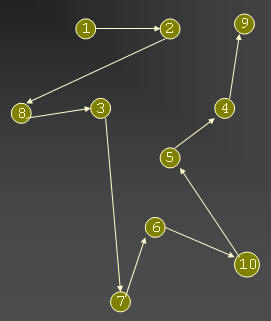
(1-2) + (2-8) + (8-3) + (3-7) + (7-6) + (6-10) + (10-5) + (5-4) + (4-9) =
3 + 4 + 3 + 4 + 9 + 8 + 5 + 3 + 3 = 42
2. Haga un cambio aleatorio a esa ruta y vuelva a ensayarla, si es mejor
entonces esa nueva ruta se selecciona, si no entonces se deja la ruta
anterior. En el ejemplo se intercambia las ciudades 3 y 4 y esta es la nueva
ruta.
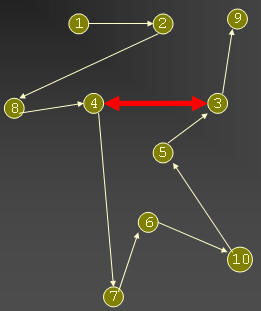
3. Determinar si es suficientemente buena la selección en caso contrario
vuelva al paso 2.
El siguiente programa escrito en C++ (compatible con Linux) implementa esta búsqueda: genera un tablero de costos al azar y luego busca la ruta de menor costo.