La búsqueda del mejor conjunto de ecuaciones y su orden
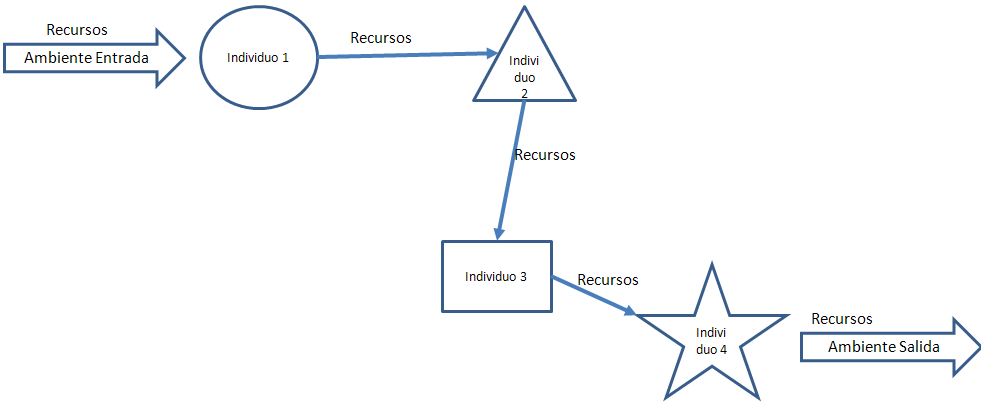
1. Cadena trófica. El ambiente deposita recursos que el individuo 1 capta, el cual al consumirlos o usarlos produce o desecha una serie de recursos que un segundo individuo consume y así sucesivamente por diversos individuos hasta que son liberados al ambiente.

2. Lo ideal para todo individuo vivo es que sus desechos sean eliminados del ambiente donde vive porque de lo contrario el individuo morirá porque se ahoga en recursos no aprovechables o hasta tóxicos para este.
3. Hay un ambiente que deposita ciertos recursos y hay un ambiente que toma otros tipos de recursos y se los lleva.

4. Con el tiempo el ambiente de entrada llena el escenario con recursos que no se retirarán hasta que no exista un ambiente que los retire, o un ser vivo que los consuma
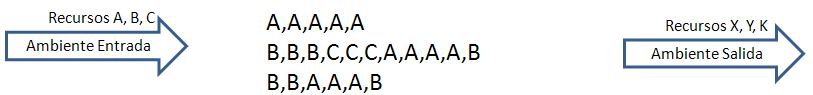
5. Si situamos un ser vivo en el escenario que consuma un tipo de recurso como A y produce como desecho a H, esto ocurriría.
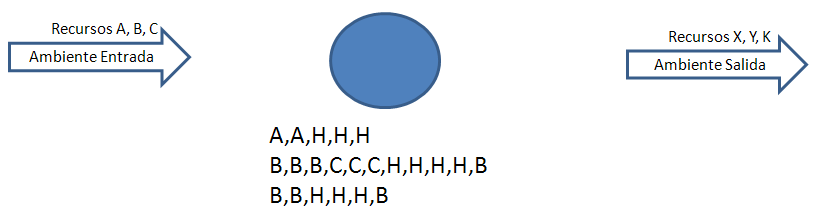
6. Finalmente nuestro ser vivo se ahoga en sus propios desechos y termina muriendo. Necesita solucionar eso.
7. Un segundo ser vivo consume el desecho H del primer individuo convirtiéndolo en otro desecho, en el ejemplo llamado K
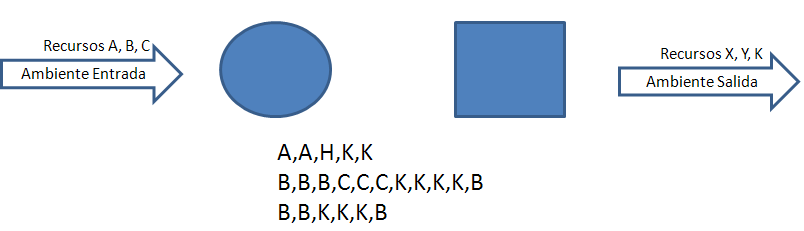
8. Afortunadamente para el segundo individuo, el desecho K se lo lleva el ambiente de salida. En caso contrario el segundo individuo moriría ahogado por el desecho K, y al morir este, el primer individuo empieza a ahogarse en su desecho H, dando como resultado que todos mueren.
9. La pregunta es: ¿Qué se da más en la naturaleza? ¿Cadenas largas tróficas o cadenas muy cortas tróficas?. Aquí si es visible el concepto de complejidad porque entre mas especies existan en la cadena trófica (es decir es mas larga la cadena), mas complejo es el sistema.
10. ¿Cómo simular un ambiente de entrada, un ambiente de salida e individuos que se relacionan en una cadena trófica?
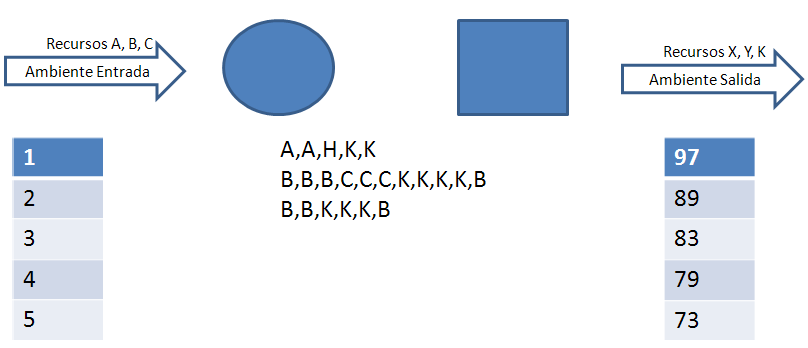
Solución:
Ambiente de entrada son una serie de valores de entrada
Ambiente de salida son una serie de valores de salida
Individuos son ecuaciones: La salida de una ecuación es la entrada de la
siguiente ecuación
11. Se usa una técnica del método Monte Carlo que es la búsqueda del camino de menor costo pero en vez de situar costos en la tabla, se ubican diversos individuos distintos. Cada individuo representa una ecuación diferente.
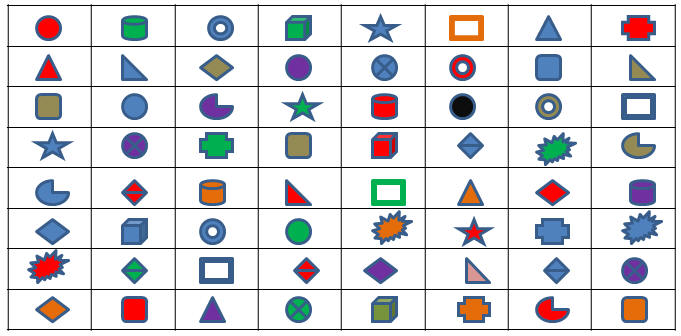
12. Se genera una relación trófica al azar seleccionando una serie de individuos
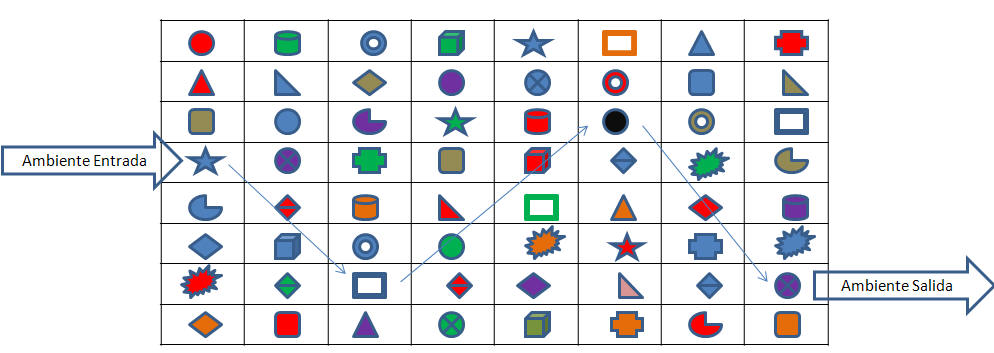
13. Se evalúan los números que entran con los números que salen.
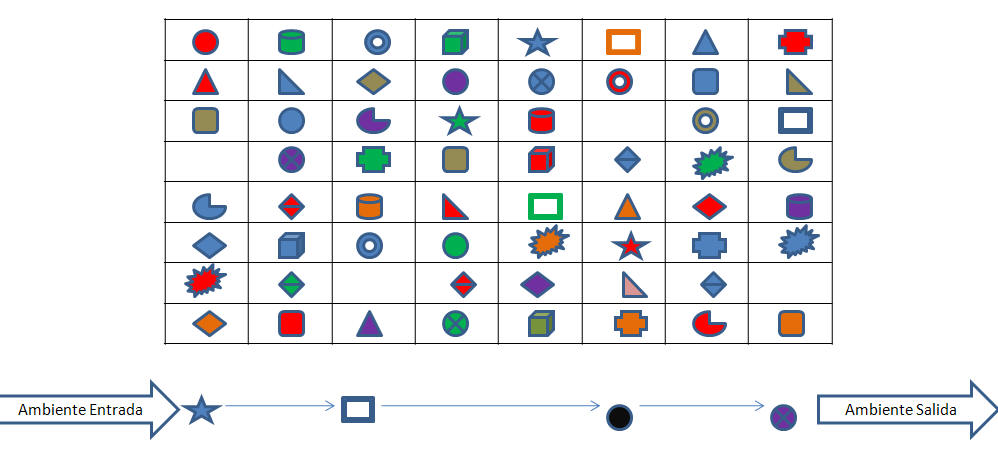
14. La Y (variable de salida) es la entrada X del siguiente en la cadena trófica
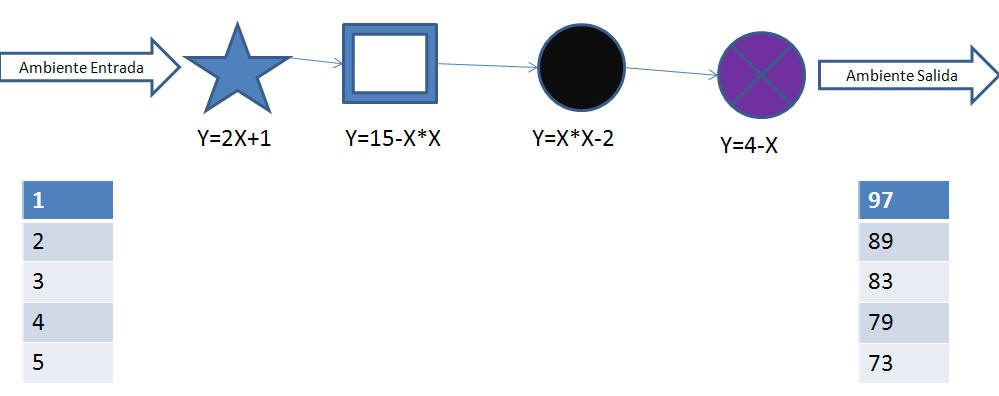
15. Se compara lo que emite el último individuo con la salida esperada (lo que se lleva el ambiente de salida). La diferencia debe ser mínima y en caso ideal debe ser cero.
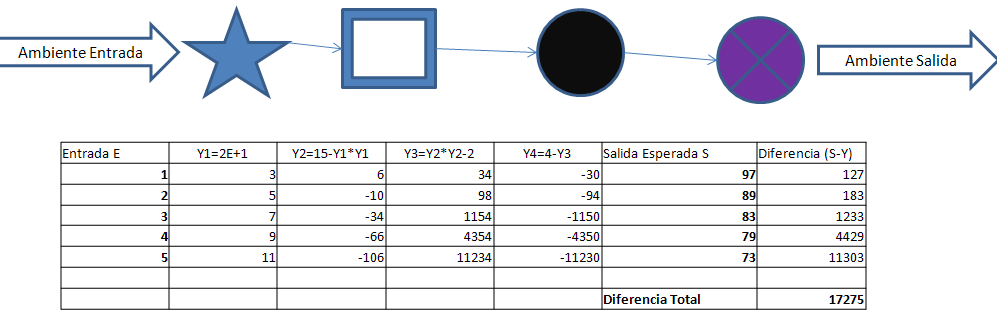
16. Se cambia algún individuo de la cadena trófica. Si la Diferencia Total disminuye, se adopta la nueva cadena trófica, caso contrario se vuelve a la cadena trófica anterior.
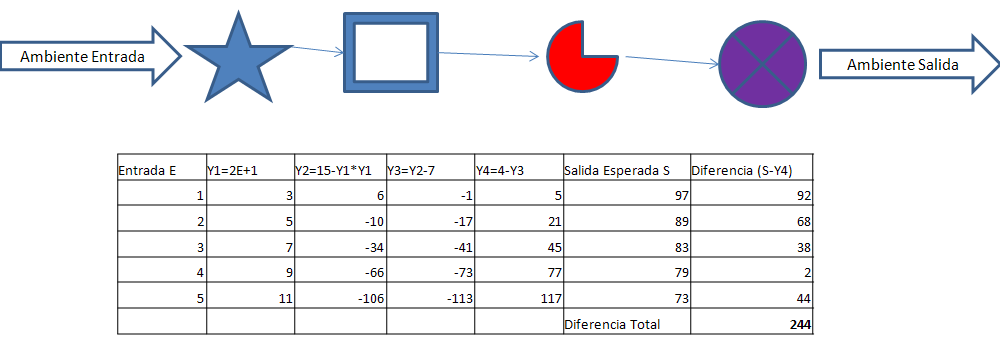
17. Las pruebas se hicieron generando cadenas tróficas de 2, 3, 4, 5, ...., 22 individuos. Las simulaciones se ejecutaron varias veces para ver cual tenía el mejor comportamiento. Se hicieron tres tipos de pruebas:
a. Con salida ascendente
ENTRADA=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,;
SALIDA=2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,;
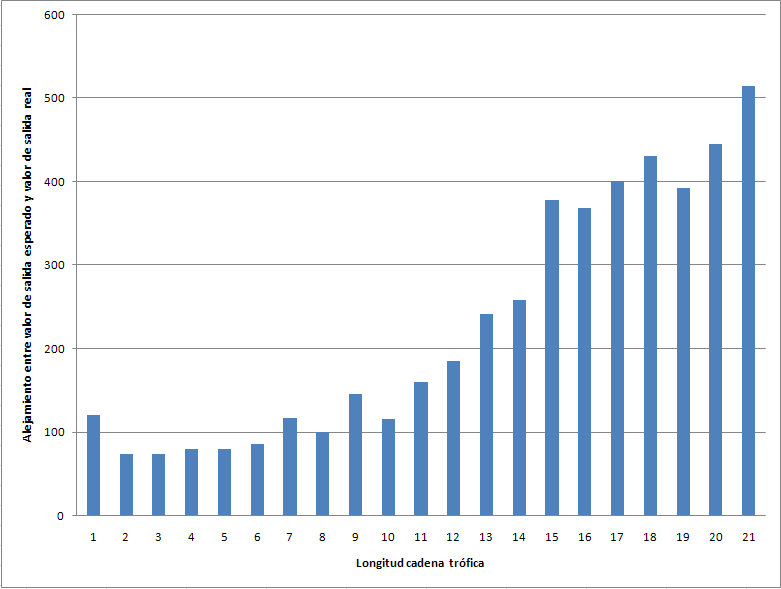
En la gráfica entre mas baja sea la barra, menor es la diferencia entre el valor de salida esperado y el valor de salida de la cadena trófica, luego es mejor. En longitudes de 2 a 6 individuos se encontraron buenos resultados pero se nota que los resultados caen desde el individuo 11 en adelante.
b. Con salida descendente
ENTRADA=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,;
SALIDA=97,89,83,79,73,71,67,61,59,53,47,43,41,37,31,29,23,19,17,13,11,7,5,3,2,;
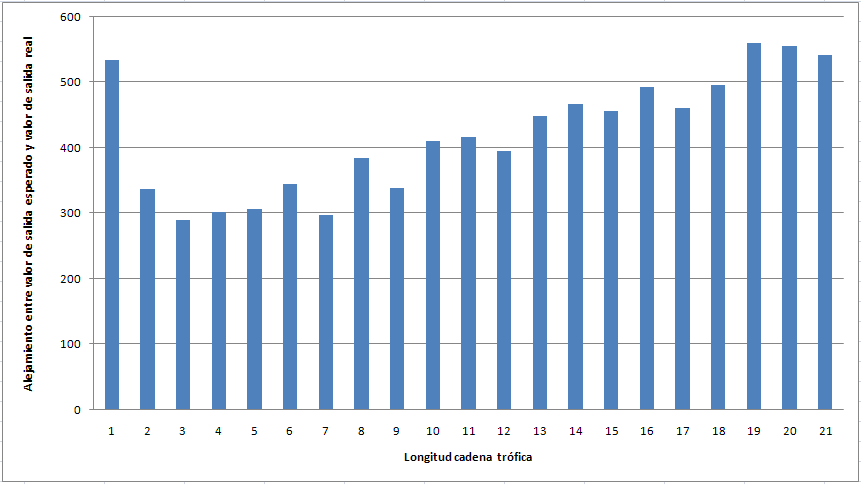
Similar a la gráfica anterior, en este caso, entre 2 y 5 de longitud hay mejor comportamiento, sin embargo el resultado fue peor que con cadena ascendente.
c. Con salida que alterna
ENTRADA=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,;
SALIDA=1,-2,3,-4,5,-6,7,-8,9,-10,11,-12,13,-14,15,-16,17,-18,19,-20,21,-22,23,-24,25,;
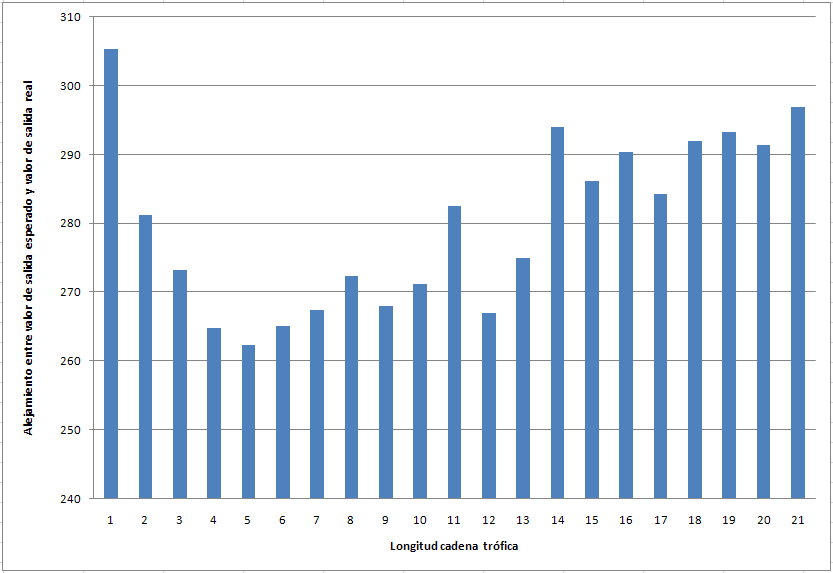
En este caso, similar al anterior entre 4 y 7 fue el mejor comportamiento.
Todas las pruebas se hicieron con ecuaciones cortas de 4 a 6 caracteres, por ejemplo, Y=X+13 o Y=8-X*X
La pregunta que se hacen son las siguientes:
1. ¿Influye el tamaño de las ecuaciones?
2. Si en vez de cambiar solo un individuo en la cadena trófica, se cambian
dos o tres, ¿hay mejoras?
3. Una vez tenga la mejor cadena trófica, con unas leves mutaciones ¿se
podría mejorar esta cadena?
En la siguiente actualización se hacen mas pruebas para responder esas preguntas.