MMIX can proceed not only integer but
floating point numbers also. The well-known IEEE (Institute of Electrical and Electronics Engineers) Standard 754 is used for this purpose.
Note that the same floting point standard is used in all Intel FP co-processors, so you can boldly use any of numerous resources about this topic.
There are some basic ideas to store floating point numbers:
- every number is presented by 2 parts called fraction (or
mantissa) and exponent (or order); the first one
stores all significant digits of the number and the last one shows
the position of floating point
- among many possible representations there are one dedicated form called normal; all numbers are always stored in normal form if possible; it will be shown later that the first binary digit in normal form must always be 1 - so computer may not store this bit in memory (hidden bit)
- every decimal number (if it's not too large) can be converted one-for-one into binary floating point number; because this procedure is approximate, two near numbers may generate exactly the same value (you must always keep this fact in your mind trying to compare floating point numbers!)
- situation when large numbers can't be presented with available binary digits is called overflow; an opposite case, when small number is so close to 0 that the difference can't be seen in available binary exponent, is called underflow; as you feel, the last case is less tragic
- not every binary code corresponds to floating point number: for example, some special combinations, called NaN ("Not-a-Number"),
denote infinity and some other specific float results
- several floating point formats may exist according to the number of bits in mantissa and order
Let's discuss some details.
The exponent representation of numbers is widely used in many branches of science to write very large or very small numbers. For example, the mass of electron is 9.11*10-31 kg, the constant value, equal to the number of atoms in a gram mole of any chemical substance, - 6.02*1023 mol-1, etc. Such way to represent numbers has a special name - scientific notation.
It's evident, that every number has many representations in this notation, for example:
6.02*1023 = 60.2*1022 = 0.602*1024 = ...
To determine some single form, the following conditions for mantissa M are used:
1/R <= M < 1, where R is radix (10 for people and 2 for computer)
Numbers, determined by these rules, are called normalized. The only one normalized form for our above example is shown by green font color.
It's curious, that 0.0 can't be normalized! Note also, that +0.0 and -0.0 has different binary codes - this is one of the reasons to use special compare instruction for float data.
Normalization is aimed on saving maximum significant digits in the fixed number of bits. It's very important that for R = 2 (binary numbers) M >= 1/2 so its first digit must be 1! This consistent pattern allows computer not to store this leftmost bit in memory, but save one more bit of mantissa to enlarge numbers precision. Such method is named hidden bit. By the way exactly the number of bits in mantissa determines a calculation precision.
The number of bits in exponent has a great influence with numeric range of computer. For instance with 11-bit order it lies approximately between 10-308 and 10308. "Denormal numbers" makes this range wider (from 10-324 to 10324) but with fewer bits of precision.
IEEE standard also defines some special codes with all exponent's bits set to 1 - so called NaNs. They include positive and negative infinity, undetermined value and some other specific values. We'll not discuss this material in details just mention once more that not every binary code is correct float number (see also the table with examples below).
Standard bit assignment for floating point numbers in MMIX is the following:
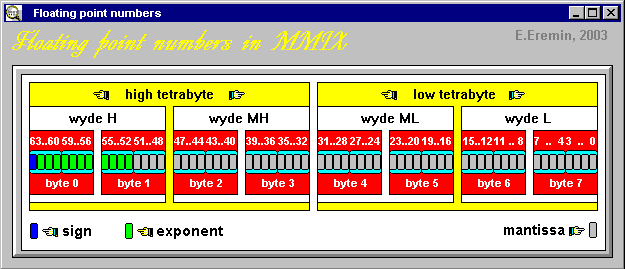The leftmost bit of 8-byte MMIX data code is the sign of a floating point number (0 - positive, 1 - negative). Next 11 bits means exponent, and the last 52 bits form mantissa.
Please note that for IEEE standard such 64-bit representation was called "double", but for MMIX it's the usual floating data format. MMIX also supports "short" 32-bit float format, which was in IEEE standard called "single". Don't be tangled!
Unlike integer numbers, float mantissa is always stored as positive value. Number's exponent is also positive, being calculated by formula:
e = o + 3FF16
where stored exponent is designated as e and o is factual number's order (can be negative!). The additional constant value is usually called bias.
And now some characteristic examples of MMIX floating coding:
| 0.5 | 3FE 0000000000000 |
| 1.0 | 3FF 0000000000000 |
| 2.0 | 400 0000000000000 |
| 4.0 | 401 0000000000000 |
| 8.0 | 402 0000000000000 |
| 10.0 | 402 4000000000000 |
| 100.0 | 405 9000000000000 |
| 1 000.0 | 40C 3880000000000 |
| 1 000 000.0 | 412 E848000000000 |
| 0.000 001 | 3EB 0C6F7A0B5ED8D |
| -1.0 | BFF 0000000000000 |
| -10.0 | C02 4000000000000 |
| +0.0 | 000 0000000000000 |
| -0.0 | 800 0000000000000 |
| maximum normalized (+) | 7FE FFFFFFFFFFFFF |
| minimum normalized (-) | FFE FFFFFFFFFFFFF |
| positive infinity | 7FF 0000000000000 |
| negative infinity | FFF 0000000000000 |
| undetermined value | FFF 8000000000000 |
| one of SNaN values | FFF 7100000000000 |
| one of QNaN values | FFF 8100000000000 |
| one of denormal numbers | 000 FFFFFFFFFFFFF |
Related topics:
"MMIX basics" page
|
Floating point numbers