
Şuna da dikkat edin ki bu çözümde hiçbir taş yenmemiştir.
akla ziyan > zeka > doğal zeka soruları
Bu bölümde kolayca akla gelebilecek fakat o derece kolay çözülemeyecek soruları inceleyeceğiz. Ben bu tip sorulara doğal zeka soruları diyorum.
1. Güzel çarpmalar:
0 hariç bütün rakamlar:
3. Satrançta doğal sorular:
Satrançta olası en kısa matı çoğunuz biliyorsunuzdur. Beyazın yardımıyla siyahın gerçekleştirdiği bu iki hamlelik mat şöyledir:

Şuna da dikkat edin ki bu çözümde hiçbir taş yenmemiştir.
4. Saat soruları:
Bir saatin akrep ve yelkovanı 24 saat içinde kaç kez üstüste gelir?
Bir dakikada akreple yelkovanın arasındaki açı 5.5 derece değisir. Buradan
hesap yapılırsa cevabın 22 olduğu görülür.
Benzer bir soru da şudur: Akreple yelkovan 24 saat içinde kaç kez birbirine dik olur?
Cevap 44'tür.
5. Küreler:
Bir kürenin etrafına, ona temas edecek şekilde, onunla aynı büyüklükte kaç küre yerleştirebilirsiniz?
Bu sorunun kesin cevabını bilmiyorum. Bayaa bir hesaptan sonra 12 olması gerektiğine karar verdim, ama bu cevap yanlış da olabilir. Bu soruyu çözerseniz bana yollayın, yayınlayayım.
Aynı soruyu iki boyutta, dairelerle sorarsak cevap 6 oluyor ve bu kolayca bulunuyor. Hatta aynı soruyu bir boyutta da sorabiliriz, cevap iki çıkar.
Soru bitmedi. Peki benzer bir soru dört boyuttaki hiperkürelerde
sorulsa cevap ne olur. Bu cevap genel olarak n boyut için nedir? Bulunabilir mi?
5. Kareler:
Bir kareyi minimum kaç farklı kareye ayırabilirsiniz? Ya da bir dikdörtgeni?
Bu sorunun dikdörtgen için cevabı 9 olarak bir kitapta vardı, ama daha iyisi bulunmuş mudur bilemiyorum. Kare için ise cevabın 21 olduğu, hem de elektronikten devreler teorisi yardımıyla, ispatlanmış.
İşte dikdörtgeni minimum sayıda kareye ayırma rekoru (9 kare):
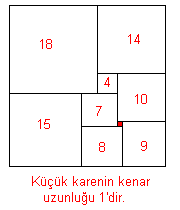
İşte kareyi minimum sayıda kareye ayırma rekoru (21 kare):
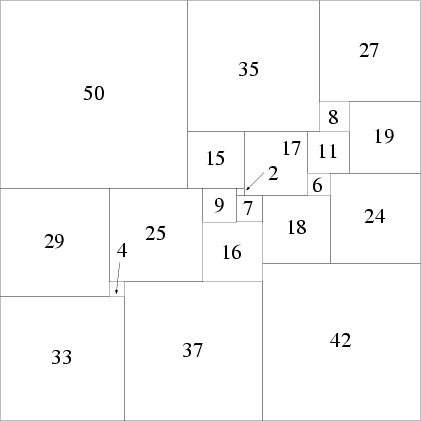
6. Dama:
Türk damasında dam olmuş (yani terfi etmis) bir taş (yani sınırsız her yöne gidebiliyor), 8x8'lik bir tahtada, en fazla kaç taşı alabilir bir hamlede? Mesela 30 beyaz taş koyun tahtaya, siyah damı da öyle bir yere koyun ki bütün beyaz taşları bir hamle içinde alsın. Bildiğiniz gibi damada uzerinden atlanan taş yeni bir taş alınmadan önce tahtadan kaldırılıyor, boylece yeni taşları yemeye uygun bir ortam oluşuyor.
Cevabı bilmiyorum. Cevaplarınızı gönderirseniz yayınlayabilirim.
7. Sayılar:
(Bu soru TZV Oyun'99 Yarı Final sınavında çıktı.) Bir A tamsayısı var. Bunun basamaklarını tersten okuduğumuzda elde ettiğimiz sayı B olsun. B sayısı A sayısını kalansız bölüyor. Bu şartı sağlayan sayılar nelerdir?
Bu şartı sağlayan bütün sayılar:
1089 x 9 = 9801
10989 x 9 = 98901
109989 x 9 = 989901 ve benzeri...
ya da:
2178 x 4 = 8712
21978 x 4 = 87912
219978 x 4 = 879912 ve benzeri...
Şuna da dikkat edin ki, 2178 sayısı 1098'in 2 katıdır.