

The standart way to implement octave up effects is by use of a full wave rectifier (FWR for short). This includes all the Octavias, the Green Ringer, the Univox Super Fuzz, among others. Let's see how it works:
To say that a note is an octave higher in comparison with another means that its fundamental frequency (that determines the pitch) is twice that of the lower one. For instance, an A played at the 1st string, 5th fret has a fundamental frequency of 440 Hz. An A played at the 1st string, 17th fret (one octave above the first one) has a fundamental frequency of 880 Hz (two times 440). The fundamental frequency is the rate at which the waveform repeats itself. Let's see it:
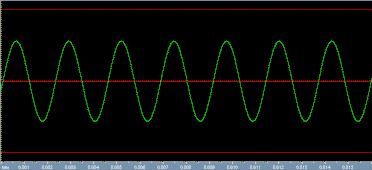
This is a 440Hz sine wave. It is periodic: it goes smoothly up, then smoothly down, and repeats it all over again. The complete signal repeats 440 times every second, so its frequency is 440Hz.
Someone noted that if the lower part of the sine wave were mirroed then we would end with a wave that is not so smooth but is still periodic, and that repeats itself twice as fast than the original wave. This mirroing is done by a FWR.

Hear a 440 Hz sine wave followed by a FWR version. Notice that it indeed goes one octave higher, but the sound is buzzier - that's because the FWR wave is not as smooth as the original signal. If you're listening to the .mp3 samples with WinAmp, the "spectrum analyzer" visualization option can be very instructive in showing how the frequency content goes higher and also spreads out.
There are other ways to achieve an octave up effect. From math, we know that if we square a sinusoid we get a sinusoid with twice the frequency. This is the basis of RG's MOS Doubler (that uses a matched MOSFET differential pair as a squaring device) and most doublers based on analog multipliers. The advantage is that the output is much smoother than in a FWR design, so it will sound "cleaner".

Hear our sine wave followed by the squared version. Notice that it goes one octave higher, and the sound is as smooth as the original. In fact it can be too smooth (it may sound dead) and we may need to add some (soft) distortion - like in RG's MOS Doubler to get a richer sound.
So far we've only considered sine waves. The signal that comes from a guitar pickup is very different from a sine wave. Hear an A440 played at the 1st string, 5th fret in a solidbody guitar, .009 string set and neck pickup. It sounds much richer than a pure sine wave, so it must have a more complex looking waveform. Below is an ampliatiotion of the sustaining portion of this note.
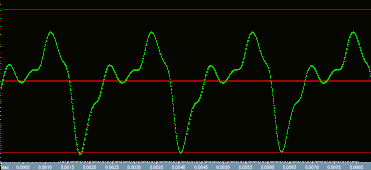
The FWR and squarer did a reasonable job with the sine wave, but how do they peform with an actual guitar note? Let's see it and hear it.
Below is how the FWR guitar note waveform looks.
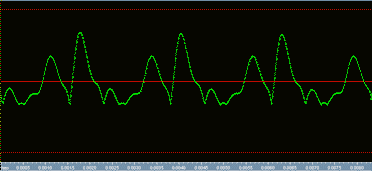
The resulting waveform is different from the original, but its fundamental frequency is not doubled. It still repeats at the same rate. We tend to hear it more like an increase in the harmonic content of the original note (distortion) than like a note an octave higher. Hear the "normal" note followed by the FWR note and judge for yourself.
Below is how the squared guitar note waveform looks.
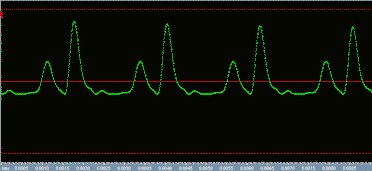
This is a little smoother than the FWR, and will sound cleaner, but the octave effect is not as pronounced as we would like. Hear it.
If we want to get a clean and pronounced octave up effect, we need to "clean" the signal before we apply it to the FWR or squarer. The simplest way to do this is use the neck pickup, roll off the guitar's tone knob and play softly. If you use a more complex filter, you can remove the unwanted harmonics in a more effective way. If we use a 3rd order active low pass filter with a corner frequency of 700 Hz (like the one used in EH MicroSynth) we keep frequencies up to 700 Hz untouched and attenuate 18 dB for each octave above it. The choice of the corner frequency and the order of the filter will determine the range of the fretboard at which you can get a good octave effect. Here's our guitar note processed by such a filter.

It's "almost" sinusoidal. It will sound "dead" like a sinusoid. Hear it.
Here's this filtered note through a FWR.

Hear it. The octave is much more evident.
Now the same using a squarer.

Hear it. Again the octave is evident, but the sound is cleaner. In fact it was too clean (it sounded lifeless) using just the squarer, so for the sound sample I runned the resulting signal through a soft distortion unit (like what's done in RG's MOS Doubler).
Here is the filter schematic if you want to try it. There are two versions: op-amp and transistor based.

You can also try it before an octave down pedal or a fuzz unit.
Here's a list of schematics for octave up effects on the web:
Tone Frenzy has a lot of sound samples and reviews of classic effects.