歐拉
萊昂哈德．歐拉(Leonhard Euler, 1707 - 1783)，生於瑞士，是人們公認的，十八世紀最優秀的天才數學家。他的父親是牧師保羅．歐拉(Paul Euler)。保羅希望萊昂哈德能從事神職工作，而萊昂哈德亦順從他的意思，修讀神學及希伯來語。
但是，曾經教授老歐拉數學的伯努利(Bernoulli)，意識到數學界將會失去一個奇才，於是便勸保羅允許萊昂哈德放棄神職工作而去鑽研數學。這才使到數學進入一個新紀元。
萊昂哈德．歐拉不久便離開瑞士，到柏林和聖彼得堡去了。在1727年，他發表了他的首篇論文：有關船桅定位的論文。
當時的當權者極需要學者去解決應用數學問題。歐拉在俄國沙皇處開始他的數學生涯。隨後到了柏林，最後又回到俄國女皇那裡渡過其餘下的歲月。
歐拉有令人難以置信的直覺和記憶力。據說他能夠在腦海裡列出一大堆完整無缺的算式而毋須寫在紙上。故被譽為『分析的化身』。有一趟，他的兩位學生在做一個極複雜的計算，可是他們的答案在第50個位有所偏差。歐拉將整個計算心算了一遍，結果找出了那個錯誤。
歐拉被譽為能解決任何問題的人。有一次，有個哲學家兼無神論者狄德羅(Denis Diderot)意圖令俄國人變成無神論者。俄國女皇葉卡捷琳娜請曾修神學的歐拉中止他的主意。於是便出現了一場神學辯論。歐拉在女皇及群臣之中宣佈：
『先生，
，因此上帝存在；請回答！』由於狄德羅不諳代數，無法與這位全歐洲最偉大的數學家辯駁，於是憤而離開俄國，返回巴黎。歐拉又重新研究神學，並提出了幾個關於上帝本性及人的靈魂的模擬證明。
一個更為燴炙人口的問題，便是『哥尼斯堡(Konigsberg)七橋問題』。這城市建在普雷格爾河邊（如圖）。
當地的居民便想道：『我們可否設計一個行程，能穿越所有七條橋而毋須重複走過一座橋？』但是他們試了很多次都失敗了。於是他們便請歐拉為他們找出一條成功的路線。歐拉也找不出這條路線，但他卻成功地證明了不可能有這樣的一條路線。他巧妙地將地圖簡化，把陸地記為點，河流則記為線（見圖）。一點連有奇數條線的叫『奇數點』，而一點連有偶數條線的叫『偶數點』。他論證說，為了進行一次成功的旅程，一個點應連有偶數條線。原因是：一個人必須由一座橋進入而以另一條橋離開，除非該陸地是起點或終點。在旅程開始時，那人衹需用一條橋離開；旅程完結之時，亦僅用一座橋讓他進入。也就是，在起點與終點不同的情況下，有兩點是奇數點。當起點與終點相同，則所有點均是偶數點。
歐拉於是作出結論：對於任何網絡，如果所有點都是偶數點，或只有兩點是奇數點，那麼才可以『一筆畫』。在哥尼斯堡的情形，四點都是奇數點－－三點連有三條線，和一點連有五條線。就是這樣，歐拉以這個簡單而絕妙的方法圓滿地解決了七橋問題。七橋問題不但激發歐拉去尋找一條關於任何網絡的基本定理，還導致一個數學分支的產生－－拓撲學(topology)。這條基本定理就是『歐拉網絡公式』：
V + R - L = 1
其中V代表網絡中交點/頂點的個數，L代表網絡中連線的條數，R代表區域數（即圍成部分的數目）。
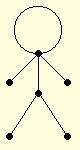
例如右方的『火柴人』，明顯可見，V = 6，L = 6，R = 1（因只有一個圓形）。代入歐拉公式，6 + 1 - 6 = 1。
至於有關的證明則從略。
『eix = cos x + i sin x』，或者是『eip + 1 = 0』，是否似曾相識呢？又或是反問：甚麼是e？這條著名的，巧妙的方程便是『歐拉方程』(Euler's Equation)。
它的巧妙之處，在於將算術最重要的 1 和 0，歐氏幾何學中的 p（下次詳談），複數的根本 i 和自然對數 e 五大種數共冶一爐。在此，本人先簡略介紹 i 和 e。
i 的定義：i2 = -1 （切記：不是 i = (-1)的平方根）。
i 的基本特性：| i | = 1；arg(i) = p/2。
e 的定義：[1+(1/x)]x，x趨向無限大。
e 的基本特性：如果 f(x) = ex，f'(x) = ex = f(x)；如果 f(x) = loge x，f'(x) = 1/x。
以下便是『歐拉方程』的證明：
