Non spaventatevi per il titolo di questo paragrafo: non vuole essere una dotta disquisizione matematica del problema.

Per chi vuole approfondire l'argomento, rimando agli articoli a firma dell'Ing. Bruno Burian pubblicati sulla rivista "Bridge d'Italia" qualche anno fa.

Ulteriori elementi sulla legge della simmetria e sulla regola della scelta ristretta verranno forniti nei prossimi paragrafi.
Ciò che mi preme che sappiate sono le conclusioni a cui si è giunti applicando al Bridge il calcolo delle probabilità relativamente alla ripartizione dei resti ed alla dislocazione degli onori mancanti.
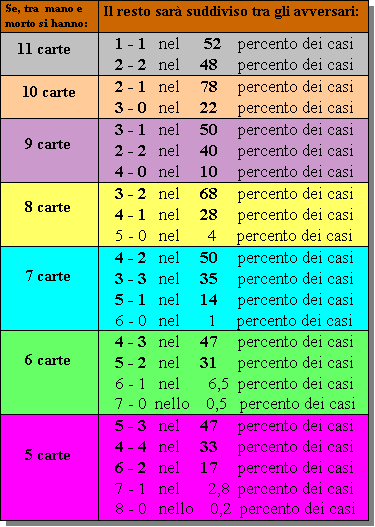
Alcune regole sono state già anticipate illustrando come si doveva muovere un colore in cui si avevano alcuni onori, per catturare quelli mancanti. In questa sede verranno riportate le probabilità delle ripartizioni dei resti e verranno illustrati alcuni esempi significativi.

I dati riportati nella tabella a lato (sono stati evidenziati in neretto i dati più importanti che sono da memorizzare) sono molto utili sia al difensore sia al dichiarante per conoscere in anticipo le probabilità di riuscita di un certo tipo di gioco (affrancamento di un colore lungo, possibilità di ricevere tagli, impostazione di giochi di sicurezza, di impasse, di rovesciamento al morto ecc.).
La prima cosa da tenere presente, comunque, è che bisogna rifarsi al principio della probabilità solo quando non ci sono altri indizi per ricostruire la distribuzione delle carte e degli onori mancanti.
Se nel corso della licitazione gli avversari hanno o no licitato, le informazioni che ne derivano sono molto più importanti che non il calcolo di astratte probabilità.
Se invece la licitazione non vi ha fornito informazioni di sorta, allora dovrete tener presente i risultati cui si è pervenuti applicando il calcolo della probabilità e sperare che le carte siano distribuite nella smazzata in corso così come ipotizzato.

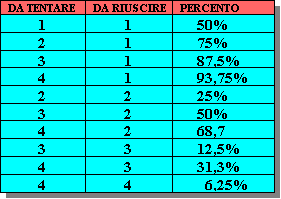
Altra tabellina da tenere presente è quella riportata a fianco, in cui sono illustrate le probabilità di giochi basati su uno o più impasse o espasse.
A volte può capitare di fare un uso contemporaneo delle due tabelle, sia per fare un raffronto, sia per calcolare le probabilità totali di riuscita di due possibili linee di gioco diverse.
Un giocatore vincente al tavolo è quello che ha un qualche cosa in più degli altri pur ottimi giocatori e questo qualcosa può essere a volte anche la padronanza che egli ha di fare un po' di conti.

Vediamo ora qualche esempio che servirà a chiarire i concetti espressi.

Qual è la probabilità di realizzare quattro prese nel colore?

Perché l'evento si verifichi è necessaria la concomitanza di due eventi: che il Re sia in Ovest (50% di probabilità) e che i resti siano divisi 3-3 (36% di probabilità).
La probabilità richiesta è una probabilità composta data dal prodotto delle probabilità semplici dei due eventi, quindi:
                                                                                                50% x 36% = 18%.

Qual è la probabilità di realizzare due prese nel colore?

Perché l'evento avvenga è necessario che si verifichi almeno una delle seguenti condizioni:
a. - che almeno uno degli onori mancanti sia situato in Ovest (75% di probabilità);
b. - nel caso che ciò non avvenga (25%), che i resti nel colore siano divisi 3-3 (36% di probabilità).
In definitiva, la probabilità totale è data dalla somma delle probabilità che competono ai due eventi, ed è precisamente:
                                                                                                75%+(25% x 36%) = 84%

Qual è la probabilità di realizzare cinque prese nel colore?

Perché l'evento avvenga è necessario che si verifichino entrambe le seguenti condizioni:
a. - che entrambi gli onori mancanti siano situati in Ovest (25% di probabilità);
b.- che i resti nel colore siano divisi 3-3 (36% di probabilità).
In definitiva, la probabilità totale è data dal prodotto delle probabilità che competono ai due eventi, ed è precisamente:
                                                                                                25% x 36% = 9%

Perché l'evento avvenga è necessario che si verifichino entrambe le seguenti condizioni:
a. - che entrambi gli onori mancanti siano situati in Ovest  (25% di probabilità);
b. - che i resti nel colore siano divisi 3-2 (68% di probabilità).
In definitiva, la probabilità totale è data dal prodotto delle probabilità che competono ai due eventi, ed è precisamente:
                                                                                                25% x 68% = 17%

Prima di proseguire il discorso, voglio sottolineare il fatto che, se si gioca in duplicato, è da preferire, fra diverse linee di gioco, quella che assicura il mantenimento del contratto rispetto alla linea di gioco che comporta una percentuale del 99% di una presa in più ma con un piccolo rischio (anche se dell'1%) di caduta del contratto.
Questa seconda linea di gioco sarà invece da preferire in un torneo per coppie tipo Mitchell.
Vediamo ora qualche esempio del tipo di ragionamento che dovrebbe fare il dichiarante nel formulare il piano di gioco.

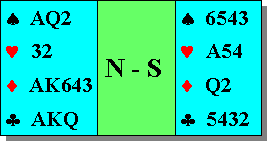
Nel diagramma a lato, Sud è pervenuto al contratto di 3 S.A., senza che gli avversari siano intervenuti nella licita. L'attacco è di Dama di cuori, lisciata dal dichiarante, sulla quale Est dà un segnale di gradimento. Ovest ritorna a cuori con il Fante ed Est risponde con una carta media. Come deve giocare il dichiarante, lisciare ancora o prendere al 2° giro?
E successivamente, come deve sviluppare il proprio gioco: giocare sull'affrancamento delle quadri o delle fiori, oppure fare l'impasse al Re di picche?
Visto che gli avversari non hanno parlato, qual è la linea di gioco che consente di ottenere la più alta probabilità di riuscita e la più bassa di caduta?

Il conto non è facile, ma proviamo a farlo ugualmente.
Innanzi tutto, supponiamo che il dichiarante decida di lisciare anche al secondo giro per cercare di interrompere le comunicazioni fra i difensori (dopo il gradimento di Est al primo giro, il fatto che sul secondo giro Est non si sia sbloccato, fa ritenere probabile che le cuori siano divise 4-4 oppure 3-5 con la quinta in Est).
Finalmente Sud prende al terzo giro di cuori, con Est che risponde nel colore. Per vedere le probabi lità delle ripartizioni 4-4 o 3-5 nel colore di cuori non dovete andare a vedere nella prima tabella di pagina 24 per resti di 8 carte nella quale abbiamo per la 5-3 una probabilità pari a P%=47% e per la 4-4 una probabilità P%=33%.
Le percentuali che troviamo nella tabella sono calcolate a priori e sono valide prima che siano stati giocati tre giri: dobbiamo escludere le distribuzioni 6-2, 7-1, 8-0.
Dovremmo applicare il teorema di Bayes per trovare le probabilità modificate dal fatto che si sono verificati alcuni eventi; il calcolo sarebbe complesso, cosa che non potete fare in torneo.
E allora? Vi consiglio di ricorrere a questo stratagemma: sono uscite 11 carte, ve ne mancano all'ap pello ancora due.
Nel primo settore della tabellina vedete che saranno distribuite 1-1 nel 52% delle volte e 2-0 nel 48%. Stabilite allora tali probabilità base, vediamo quali sono le possibili linee di gioco del dichiarante, che ha a sua disposizione le seguenti alternative:

1. Battere 3 giri di fiori

a. Se i resti sono 3-3 (36% delle volte), Sud ha mantenuto il contratto anche se non filano le quadri in quanto rientra in mano con la Dama di quadri, gioca la fiori affrancata e colleziona almeno nove prese facendo quattro prese a fiori, tre (almeno) a quadri, una a cuori ed una a picche.            P%(a) = 36%

b. Se le fiori non filano (64% delle volte), si può sperare di  mantenere il contratto se filano le quadri (resti 3-3, 36% delle volte). La probabilità dell'evento b. è data da:        P%(b) = 64% x 36% = 23%.

c. Se oltre alle fiori (64% delle volte), non filano anche le quadri (64% delle volte), esiste ancora una consistente probabilità di portare in porto il contratto se si verifica almeno uno dei due seguenti eventi:
- le rimanenti cuori siano divise 1 - 1 (52% delle volte) e chi entra in presa a quadri ha la cuori più elevata (50%) e non ha la quarta fiori (50% delle volte);
- le rimanenti cuori siano divise 2 - 0 (48% delle volte) ma chi ha le due cuori non entri in presa con la quarta quadri (circa 50% delle volte).
La probabilità dell'evento c. è, pertanto, data da:
  P%(c) = 64% x 64% (52% x 50% x 50% + 48% x 50%) = 64% x 64% x 41% = 15%.

La probabilità totale della prima linea di gioco ipotizzata è:

2. Fare subito l'impasse a picche

a. Se l'impasse riesce (50% delle volte), il contratto è assicurato in quanto il difensore potrà fare almeno nove prese e precisamente: due prese a picche, una presa a cuori, almeno tre prese a fiori, almeno 3 prese a quadri. P%(b)= 30,14%

b. Se l'impasse non riesce (50% delle volte), il contratto è ancora fattibile se si verifica (almeno) uno dei seguenti eventi:
- che le cuori rimanenti siano distribuite 1-1 (52%) e che filino le fiori (36%) o le quadri (36%);
- che le cuori rimanenti siano distribuite 2-0 (48%) e che le abbia Ovest (50%) e che filino le fiori (36%) o le quadri (36%);
- che le cuori rimanenti siano distribuite 2-0 (48%) e che le abbia Ovest (50%), che le fiori non filino (64%) e che filino le quadri (36%);
In definitiva la probabilità dell'evento b. è data da:
  P%=50%[52%(36%+36%)+48%*50%*(36%+36%)+48%*50%*64%*36%]
  P%(b)=50%(37,44%+17,28%+5,55%)  P%(b)= 30,14%

La probabilità della seconda linea di gioco (impasse immediato a picche e poi affrancamento dei colori lunghi) è data da:

3. La terza linea di gioco è intermedia fra la prima e la seconda linea già descritte.

a. Si inizia con il provare se filano le fiori (36%). Se filano, il contratto è mantenuto. P%(a)=36%

b. Se le fiori non filano (64%), si rientra in mano con la Dama di quadri e si fa l'impasse al Re di picche (50%).
Anche in questo caso, se l'impasse riesce, il contratto è assicurato:      P%(b)=64%*50%=32%.

c. Se le fiori non sono filate (64%) e l'impasse è fallito (50%), il contratto può essere ancora mantenuto se filano le quadri e si verifica almeno una delle seguenti alternative:
- che le cuori rimanenti siano 1-1 (52%), ed Est, che ha il Re di picche, ha la cuori più elevata (50%), mentre la quarta fiori è in Ovest (50%);
- che le cuori rimanenti siano 2-0 (48%) ed entrambe in Ovest (50%).
La probabilità dell'evento c. è data da:
    P%(c)= 64%*50%*36%*(52%*50%*50%+48%*50%)
    P%(c)=11,5%*(13%+24%)=4,25%
In definitiva la terza linea di gioco offre una probabilità pari a:

Abbiamo esaminato le 3 linee di gioco ed abbiamo calcolato le probabilità relative. Il calcolo non è semplice e, sicuramente, non può essere fatto durante il gioco; inoltre, le tre probabilità calcolate non sono molto differenti ed inoltre sono state calcolate con approssimazione.

La linea di gioco da preferire è la seconda, quella che prevede inizialmente la probabilità più elevata e che non esclude altre possibilità successive.
Quello che mi preme che ricordiate è che fra l'affrancamento di un palo lungo, possibile se i resti sono 3-3, ed un impasse, conviene, generalmente, quest'ultimo, mentre tra l'affrancamento di un palo lungo, possibile se i resti sono 3-2, ed un impasse conviene l'affrancamento del palo lungo.

Vediamo ora un altro esempio facendo riferimento ad una mano non troppo difficile.
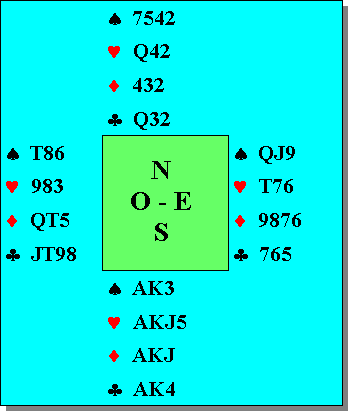
Con la mano riportata nel diagramma a lato, Sud gioca 6 S.A. e riceve l'attacco di Fante di fiori.
Il dichiarante ha undici prese di battuta (quattro cuori, due picche e due quadri). La presa mancante può venire dalla riuscita dell'impasse a quadri (50%) o dall'affrancamento della quarta picche del morto (36%).
A questo punto la domanda: come giocate per mantenere il contratto?
Facile direte voi: faccio l'impasse alla Regina di quadri perché è il gioco che mi dà la massima probabilità (50%).
Errato, dico io: dovete prima tentare l'affrancamento della quarta picche del morto (probabilità 36%), giocando però subito il colpo in bianco e non dopo aver battuto Asso e Re perché, altrimenti, potreste perdere subito due prese a picche se i resti sono 4-2.
Preso il ritorno dei difensori, battete Asso e Re di picche e, se i resti sono 3-3, come nel diagramma proposto, avete mantenuto il contratto senza aver fatto l'impasse alla Dama di quadri che vi sarebbe andato male.
Se invece le picche non filano (64%), è necessario che riesca l'impasse a quadri (50%).
In definitiva, giocherete con una probabilità pari a  P% = 36%+64%*50% = 68%,    superiore a quanto vi offre il sorpasso iniziale a quadri.

Questo perché, se iniziaste col sorpasso a quadri, e questi vi andasse male, non potreste poi tentare l'affrancamento delle picche, per conseguire il quale dovreste cedere un'altra presa.
Il tentare inizialmente l'affrancamento della quarta picche non vi precluderebbe la possibilità di fare il sorpasso a quadri nel caso che la quarta picche non potesse essere affrancata.
Prima di concludere, vi raccomando di tenere sempre ben presente la seguente regola:
Quando esistono due o più linee di gioco alternative, si devono adottare per prime, qualora sia possibile, quelle che. in caso di esito sfavorevole, non compromettano l'esecuzione di altre linee di gioco, anche se comportano minore probabilità di riuscita.
Abbiamo visto quanto una buona conoscenza delle percentuali sia essenziale per chiunque voglia migliorare il proprio gioco.
La struttura del mazzo di carte è governata da rigorose leggi matematiche che è indispensabile apprendere per poter capire il loro modo di operare. A lungo andare, infatti, contrastare tali leggi, giocare ossia contro la probabilità, non vi potrà portare nulla di buono ma solo danno e delusioni.
Questo non significa che solo i primi della classe o gli scienziati possano giocare un buon bridge.
Al contrario! Un giocatore esperto deve imparare a memoria solo le combinazioni più semplici, ma sa mettere in atto le sue conoscenze. Egli sa che un impasse riesce al 50%, che se basta un solo impasse su due per realizzare il contratto, tre volte su quattro la manovra avrà successo.
Avendo nove atout, saprà che le carte mancanti saranno ripartite 2-2 quaranta volte ogni cento contro le cinquanta volte della distribuzione 3-1. Se invece le carte mancanti sono cinque, circa due volte su tre i resti saranno 3-2 e circa una volta su tre la ripartizione sarà più sfavorevole (4-1) mentre i resti 5-0 si verificano molto raramente (solo quattro volte ogni cento).
Se le carte mancanti sono sei, circa la metà delle volte i resti sono 4-2, circa una volta ogni tre sono 3-3 ed una ogni sette sono 5-1. Solo una volta ogni cento capiterà la distribuzione 6-0.
Armato di queste cifre e di una conoscenza anche limitata delle regole del Calcolo delle probabilità, un giocatore intelligente è in grado di operare una scelta oculata fra diverse linee di gioco e, tenuti presente anche altri elementi, essenzialmente l'andamento della licita, sa scegliere quella giusta .
Le prossime volte che giocate provate anche voi a fare un po' di conti e vedete come ve la cavate!
Ed ora eccovi un nuovo modo di procedere a contare le percentuali; spesso nel corso del gioco cercherete di contare le mani dei difensori. Quando la lettura sarà completa sarà come giocare a carte viste, ma talvolta la lettura sarà solo parziale. In queste occasioni, se vi chiedete quale sia la posizione di un Onore mancante, non c'è bisogno di consultare la tabella delle percentuali per fare calcoli complicati.
Il sistema più semplice di calcolare la probabilità in simili circostanze è quello di contare il numero di caselle vuote disponibili in ciascuna delle mani dei difensori, ossia delle carte a cui non avete ancora potuto assegnare un valore.
Naturalmente nel calcolo potete utilizzare solamente i colori la cui ripartizione fra i difensori è perfettamente nota, compreso quello in esame, a patto che siano state giocate tutte le cartine.
La probabilità che l'onore cercato sia in una mano piuttosto che nell'altra è strettamente connessa con il numero delle caselle vuote di ciascuna mano.
Come al solito spero che un esempio serva a chiarirvi le idee.

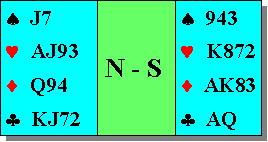
In possesso della mano descritta nel diagramma a lato, Sud gioca 4 CUORI e riceve l'attacco di Asso e Re e Dama di picche. Tagliate al morto la terza picche con il 9 ma venite surtagliati da Est con il 10.
Prendete con l'Asso il ritorno quadri e giocate cuori per l'Asso (entrambi i difensori rispondono con una cartina).
Giocate ora il Fante dal morto ed Est mette l'ultima cartina rimasta in circolazione.

Se non avete altre informazioni che vi possono provenire dalla dichiarazione degli avversari, dai punti finora mostrati o da indicazioni che possono scaturire da un determinato attacco, solo il Calcolo delle Probabilità vi può guidare in situazioni come queste, ma come vi ho detto precedentemente, non occorre fare conti particolarmente difficili.
Ovest ha mostrato di avere sei carte di picche ed una di cuori mentre ad Est sono da accreditare due carte a picche e tre a cuori: rimangono pertanto sei caselle libere disponibili per Ovest ed otto per Est.
Le probabilità sono pertanto 8 contro 6 che Est abbia la Donna di cuori e pertanto deve essere fatto l'impasse.
Ricordatevi che la tecnica di contare le caselle vuote ancora disponibili oltre a semplificare di molto i conti fornisce altresì valori precisi di probabilità validi al momento della decisione.

È pertanto un ausilio decisionale da non sottovalutare.