[MS Word, ZIP] [PDF] [Comments]

Introduction

Contemporary science has come to a clear understanding of the necessity of studying the development of any object to comprehend its structure and behavior [1]. The first intuitive idea of an object's development associates it with the growth of the object's complexity, and the existence of different levels within the object. The consideration of hierarchical structures and hierarchical systems [2] leads to the natural question: "What is the multilevel organization as such, and where it comes from?" In particular, such investigation might bring light to the problem of the distinction of structural and systemic description, which often get mixed in the literature [3]. One more goal that might be achieved in such a study is the reconstruction of the object's integrity and discovering the directions of its development, rather than focusing on arbitrary details and the peculiarities of behavior [1].

The recent interest to the study of complex systems poses, along with the numerous technical issues, many fundamental questions. What is the organization of a system? How "complex" systems differ from "simple" ones? What should be meant under the "small", "large" and "superlarge" system? Thus, the sense of complexity may differ at different levels and for different objects — and it would be desirable to have some qualitative distinctions before trying to construct any formal measures of complexity. Indeed, there are many such quantitative measures [4,5], and it is not always clear what they actually evaluate.

In many cases the answers are sought in hierarchical considerations. The literature is replete with different hierarchical constructions, and some authors suggest distinguishing the hierarchy (development) as a separate level of complexity, along with the structure (static level) and the system (dynamic level) [1]. It is well known that hierarchical organization may be the key to efficient control in large systems [6]. Yet another hint comes from nonlinear physics, considering strongly non-equilibrium systems with their own order. It has been found that the behavior of such systems may be dependent on the sequence of catastrophes they have passed to the moment of observation, and hence the history of the system would be represented in its current state [1][7]. Development and hierarchical organization were thus related to nonlinearity, self-action.

Analogous phenomena have been known in philosophy since long ago, under the name of reflection, which, however, was mostly associated with subjectivity. The recognition of the different forms of reflection might lead to a better understanding of the differences between the physical, organic and subjective levels of development. This would be one more step to the integrity of science, which has been earlier sought within structural and systemic approach [8].

Levels of integrity

Each science is dealing with its specific object, and any consideration has to start from the fundamental concepts which cannot be introduced within the science and should be borrowed from somewhere else, representing the first intuitive view of the field. On the other side, these a priori concepts outline the scope of relevant problems and delimit the range of applicability. For studying complexity, the notion of integrity might be taken for such a starting point. Thus, to speak about complexity of something, one must first insure that this "something" may be considered as an entity distinguished enough from the rest of the world. That is, the natural premise to complexity studies is the existence of integral "wholes" whose complexity could be further described. This means that complexity may only be defined in respect to that integrity, being one aspect, or one form of it.

The first, most primitive form of integrity is singularity. At this level, the object is considered as unique and isolated, without any regard for other objects. No internal organization or external relations are considered, and therefore the object is quite simple. The only definiteness it may possess is its very existence. Not much can be inferred from such a primitive consideration — still, this is the necessary first stage of any study, the recognition of the problem.

On the next level, the simplicity of this recognition gives place to the observation of external dependencies and internal inhomogeneity — this is where one can speak about complexity. The object is considered together with its environment, and the object's interaction with it leads to specific structures, processes or kinds of development. The object is no longer unique and simple, being rich enough to be studied by various sciences, from their specific points of view. The integrity of the object may therefore seem violated, being potential rather than actual, and a "metascientific" approach is required to provide a unified view.

The level of unity restores the singularity of the object retaining its complexity. The object becomes completely reflected in its environment, while this environment is completely represented "inside" the object. The features of the object are just the traces of its history, and its behavior is non-local, being controlled by the higher-level development. However, this level escapes purely scientific consideration, being essentially influenced by practice.

Now, when the level of complexity has been related to the other levels of integrity, one can proceed with unfolding the hierarchy, distinguishing different types of complexity itself. Its definition as a path from singularity to unity provides a logical basis for such a distinction. Thus, one can conclude that there are two sides of complexity reflecting its relation to these extremes, and that there should be an intermediate level linking them into a hierarchical whole.

The level of complexity extending singularity in a minimal way is multiplicity. There are many instances of the same singularity, as if produced by some cloning procedure, when each clone remains simple and isolated from the others, but not unique this time: there are many such objects, defining a specific object class by the very fact of their existence. Still, the objects of the same class enter no interrelations beyond the simple equivalence, mere belonging to the same class. Any one of them could be chosen as a representative of that class, and the whole class can be restored from every single element. Therefore, the complexity of such class may be related to the number of its elements, and the hierarchy of multiplicity coincides with the hierarchy of cardinal numbers.

The unity side of complexity might be called order, including both the sense of "being properly made, arranged", and the sense of "as it should be". In a sense, this is the "most complex" complexity, since it cannot be comprehended in the purely objective terms, being unfolded into a "teleological" hierarchy. Historically, the difference between multiplicity and order is the ancient opposition of Chaos and Cosmos — the opposition that gave birth to all the earthly things. This earthly way from Chaos (multiplicity) to Cosmos (order) is the intermediate level of complexity introducing some congruencies into the chaotic multiplicity, while leaving enough space for extensive and intensive development of the local order. This kind of complexity might be called coherence.

So, multiplicity is associated with disorder, coherence means partial order, while on the highest level order becomes complete, universal.

Moving deeper into the hierarchy of complexity, one could use the same logical scheme, distinguishing the opposite aspects of coherence joined by an intermediate level. This procedure leads to the three levels of coherence: structure, system and hierarchy.

The first category of this triad, structure, refers to internal coherence, representing the object as a collection of elements and their links. This representation is least different from multiplicity, the only new feature being the division of the multiplicity into two classes, one called "elements" and the other called "links". Being the internal characteristic of the object, structure may be thought of as the static aspect of the object.

The inverse of structure is system, the second level of coherence. It refers primarily to the external manifestations of the object, the way it "moves" in its outer space, altering its relations with the environment. Since these relations are somehow structured, system may be generally considered as the way of transforming one structure into another. So, the basic category at the systemic level is "transformation", or "transition" — and therefore system represents the object's dynamics.

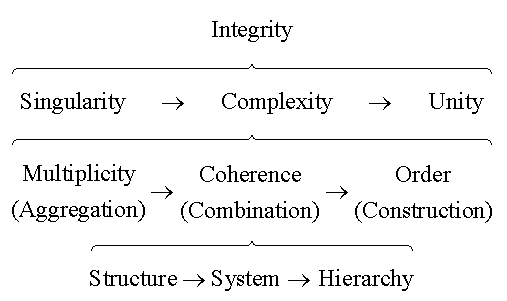
Figure 1. The hierarchy of integrity.

Logically, the next level of coherence should be the synthesis of the internal description provided by structure and the external systemic treatment. It should consider the object both statically and dynamically, so that systemic transformations lead to the internal changes in the object, which nevertheless retains some of its structural features as to remain the same in these transformations. This is the level of development — and the synthesis of structural and systemic features is hierarchy.

Thus, complexity itself becomes complex, comprising the hierarchy of possible forms (Fig. 1). One level of distinction provides the triad of multiplicity, coherence and order — on another level, one might distinguish structural complexity, systemic (functional) complexity, and hierarchical (developmental) complexity. Incidentally, this sequence reflects the history of methodological thought in the XX century: the beginning of the century was marked by the structural approach, which gave way to systemic approach in the middle of the century, while the end of the XX century passed under the dominance of the idea of development, which receives its formal expression in the hierarchical approach.

Structure

The most general idea of structure is linking some relatively distinct elements by a number of links. Typically, structure is modeled with a set and relations on it: the elements of the set represent the elements of the structure, while the links are associated with the n-tuples of the elements belonging to an n-place relation. However, the links may be treated as independent entities, like arrows in the categorial approach [9]; in this case, one needs to explicitly define the beginning and the end of each arrow. The support set may be either discrete, or continuous, or even more powerful. Accordingly, the relations may vary from the finite number of element pairs to connectivities on a non-trivial manifold. Links may be either rigid, or stochastic, or any combination of the two. All these possibilities fall under the scope of traditional mathematics, which may be called the science about structures, in general. Since structure refers to the static side of the whole, it becomes clear that mathematics is incompatible with any motion, and this explains why mathematicians made their best to expel movement (and development) from mathematical language, and even the modernistic mathematical trends (like constructivism) speak of dynamics in a static way, imposed by the traditional forms of mathematical reasoning. That is, the mathematical description of a process refers to the structure of the process only; accordingly, mathematical models of development mainly reflect its structural aspect [comment].

The simplest structure [comment]. is given by a finite set S = {s_i: i=1,...,N} with a single two-place relation L: S®S defined on it. When a pair <s_i, s_k> belongs to relation L, one says that element s_i is linked to element s_k by the link l_ik Î L. Such link is oriented, and l_ik ¹ l_ki; moreover, relation L need not contain both l_ik and l_ki, so that if one element is linked to another it does not imply that there must be a link back. Denoting the set of the elements of S which are linked to some other elements with dom(S) and the set of the elements that appear in the right-side of the pairs from L with rng(S), one can observe that, in general, dom(S) ¹ rng(S), dom(S) ¹ S and rng(S) ¹ S. In the trivial case, L is empty, and the structure reduces to mere multiplicity. At the opposite extreme, any element is directly linked to any other, and L = S².

However, structure is more than just elements and links — it is a kind of wholeness, a level in the hierarchy of integrity [comment]. In the above model, the appearance of this integrity might be described as follows.

The direct links between the elements of S represented by l Î L are not the only connections between them. Thus, the relation L may contain both pairs l_ik and l_km, which means that there is a mediated link between s_i and s_m (Fig.2a) — and this does not depend on whether there is the direct link l_im or not. Longer chains may be constructed as well, and one comes to considering the hierarchy of indirect links which is one more manifestation of the same structure.

Yet another structural feature is the formation of collateral links. For example, if both l_ik and l_mk belong to relation L, elements s_i and s_m are naturally related to each other as the predecessors of the same element (Fig.2b). Similarly, if both l_ki Î L and l_km Î L then there is a collateral link between s_i and s_m , which have a common predecessor (Fig. 2c).

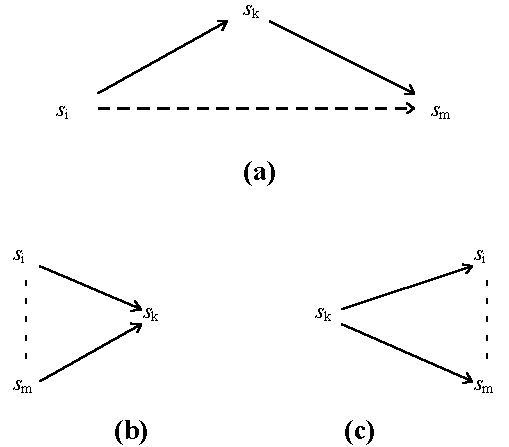
Figure 2. Indirect links: (a) mediated; (b,c) collateral.

Direct, mediated and collateral links may be combined in various ways, the numerous kinds of indirect links thus obtained being the manifestations of the same structure. If an element s Î S participates in at least one pair l Î L, it becomes, in one way or another, connected with any other such element. The elements which are not linked to any other element (or to themselves) by L are completely irrelevant to the structure, so that the set dom(S) Ç rng(S) can be considered as the set of the structure's elements in the applications, instead of S. Note the difference between irrelevant and isolated elements: the former merely do not belong to the structure, while the latter are just linked to themselves only, with no direct or indirect link to any other element.

The distinction between elements and links within the structure may be relative. Thus, if element s_k mediates the link between elements s_i and s_m, it may be considered as a higher-level link connecting l_ik and l_km. Since any two elements of the structure (discarding the irrelevant elements) are somehow connected, any element can thus become a link between links, so that the links will play the role of the structure's elements. Hence, any particular subdivision of the structure into elements and links does not follow from its own properties, but rather from some conditions external to the structural approach proper. When a number of "primary" elements and links are selected, the rest of the structure can be accordingly unfolded; for another choice, the structure will unfold differently. Such refoldability makes the structure hierarchical.

The existence of different unfoldings, with the respective levels of integrity, means that there is no universal quantitative measure of structural complexity. Moreover, even though one might evaluate structural complexity for every particular unfolding, there may be a hierarchy of different measures, not always reducible to a single number. Thus, in the simple relational model described above, one might count the total number of links and divide it by N² (the maximum possible) to obtain a kind of probability (frequency) p. Then, a global measure of structural complexity could be introduced as

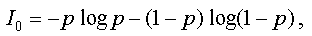
which is the well-known formula for the quantity of information. The value I₀ is equal to zero when there are no relevant elements in the structure, or for a maximally connected structure, when L = S². This agrees with the intuitive idea of structural complexity: the structures without links are quite simple, as well as the "rigid" structures with the elements linked in a "completely deterministic" way.

An alternative approach is to count the number of "arrows" beginning at a given element s_k and divide it by N to obtain the normalized values p_k lying in [0,1]. Evidently,

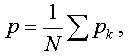
so that the "probability" p introduced via counting links is just the average "probability" of an element being linked to the structure. Since all the p_k are mutually independent, one could evaluate the information contained in the set {p_k} as

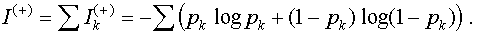
Analogously, one could define the value

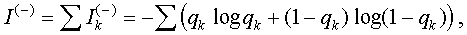
where q_k are the counts of arrows with the end at the element s_k divided by N. Though, evidently, the average frequency p may be expressed through q_k too as

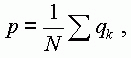
the quantities I⁽⁺⁾ and I^(-) do not coincide, and the measure I₀ becomes split into two dual measures I⁽⁺⁾ and I^(-).

Of course, the process can be continued, to account for indirect links and substructures. For example, every two elements s_i and s_k may be assigned with a numerical weight c_ik indicating the "level of connectedness" of these elements within a given unfolding of the structure. The weights c_ik can be chosen from the interval [0,1] so that c_ik = 1 if the two elements are connected in every possible (direct or indirect) way, while c_ik = 0 would mean that there is no connection between the elements, that is, the structure splits into mutually isolated substructures. Then, a gross measure of complexity can be introduced as

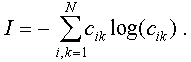
The set of weights {c_ik} may be considered as a fuzzy subset of S² [10,11]. In general, c_ik cannot be interpreted as probabilities, since they do not necessarily satisfy the "normalization conditions", as specified in [11]. However, there may be classes of valuation functions that can be associated with cumulative probability distributions [12]; the complexity measure I will become a kind of entropy in this case.

I should stress that structure as a level of coherence does not imply any restrictions on the type of elements and links. Thus, there may be "material" structures, with both elements and links of a material nature; however, there may also be completely "ideal" structures, or some mixtures of the two.

System

A typical abstraction of system might be represented by a collection of triads {<S_in, S_c, S_out>}, where S_in and S_out are the input and output structures respectively, while S_c denotes the current state of the system, often identified with its "internal" structure. Depending on the level of consideration, each of these three structures may be differently unfolded, providing the special models known in the literature. Thus, the completely folded S_c leads to the notion of "black box", which evidently correlates with the idea of elementary operation in the theory of computability [4], or with the basic arrows in the categorial approach [9]. In a more unfolded form, S_c may be any composition of such elementary operations, implementing an algorithm of "calculating" the output structure by the input structure, the "white box" [13]. Complexity on the systemic level may therefore be called algorithmic, or computational complexity [4].

One might develop a simple model of system analogous to the relational model of structure described in the previous section. Thus, S_in and S_out might be chosen from the same class of structures representing the states of the system's environment; then they will be analogous to the elements of the structure, while operators S_c connecting them will be the analogs of structural links l. The only difference is that the "elements" connected by such functional link are external to the system, unlike internal elements of the structure. This is the characteristic duality of any system: on one side, it functions like a structured object — while on the other side it can be considered as just a more detailed specification of a structural link.

The formation of mediated links finds its systemic-level analog in the external composition of systems, when the initial state S_i of the environment is transformed into the final state S_f via an intermediate state S^*:

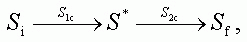
which may be considered as the construction of a new operator S_c = S_2c°S_1c. Like with structures, such sequential compositions (or cascades) can form long chains; since an elementary systemic transformation (operation) may be thought of as a transition, the composite functions represent processes. For example, the movement of a point x in a configuration space X can be considered as sequential transformation of structures:

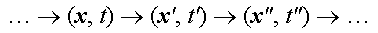
In this case, the operators transforming one structure into another must be associated with the respective elements of the tangent space TX, velocities. Such an approach is typical for classical physics, and especially classical mechanics.

The other kind of indirect links, collateral links, can be associated with the parallel composition of systems, when several input or output structures are united into a joint input/output. This means that a class of structures would serve as the system's input or output, instead of a single structure; along with the basic structures, such class would include all the possible sets composed of the basic structures. For example, a binary input is a single-element structure s ; when two such structures s and s' are composed into a parallel input, there may be combinations (s), (s') and (s,s') as the possible values of the same input. In a more complex case, one could consider some distributions of elementary inputs as the "microscopic" realizations of a "macroscopic" variable. Such parallel composition of systems is widely employed in statistical physics. Various combinations of sequential and parallel composition may be found, for instance, in quantum theory.

The external nature of systemic coherence leads to a kind of integrity quite different from the internal integrity of the structure. The system's integrity has to be comprehended from all the variety of its relations with the environment, rather than from the internal structure of the system. Generally, functional complexity is revealed dynamically, in the process of functioning [14]. Consequently, it cannot be described in a static way, and this is the main source of any problems with "computability", leading to the numerous forms of the famous Göedel theorem [15] [comment].

Systemic complexity is complexity of functioning, and it should not necessarily correlate with the complexity of the structures involved. Functional complexity is the property of a single element, or a structure as a whole, rather than of the way the elements are connected, and, in this sense, it is complementary to structural complexity [16]. For example, a computer program may be very long — but all it does is a constant output; a nail may be driven in either with a hammer, or using a complex cybernetic device, etc.

However, the complexity of the "white boxes" modeling a system would generally correlate with functional complexity if these models are built of some "standard" elements, whose functional complexity does not change when they are connected into a system. In the simplest case, the external model of a system ("white box") may be constructed of the elements of unit complexity — and then the algorithmic complexity of the composite system would be represented by the complexity of the junctions. Such systems are completely "transparent", though they do not have to be deterministic.

Still, there is a difference between the system and its model of the "white box" type. Since the goal of such modeling is to reconstruct functioning only, the model may be built of the blocks different from the "matter" of the original system — and this would allow a partial reconstruction of behavior only, with some properties of the original system discarded. That is, the original system is modeled on a definite level — and the variety of such models is the systemic counterpart for the various unfoldings of the structure. Usually, all the lower-level functioning is considered as side effect, so that different systems model each other to that accuracy. However, there is also an analog of the structure's refoldability: the properties that are considered as side effect in one situation, may be essential in another.

Like the distinction of elements and links of the structure may be relative, there is a mutability of subsystems and their junctions. Thus, for the sequential composition of two functional blocks described above, the triad <S_1c, S^*, S_2c> may be considered as a component of a system, so that the intermediate structure S^* will play the role of the internal structure of this system, rather than the state of environment. In the operator S_2c°S_1c, the junction _° (represented by the structure S^*) transforms the output of S_1c into the input of S_2c.

As in the case of structures, systems may be either material, or ideal, or of a mixed type. The definitions of this section remain applicable in each case — though the functional treatment of the system might be not evident sometimes. Thus, systematization often means mere classification, which seems to be closer to the structural level. However, taxonomy can be a system if it is used for categorization, implementing the transition from the appearance of the object to its essence, and then to its more subtle features. Still, there is no rigid boundary between the structural and systemic levels, and they usually become intricately interwoven in practice, representing the two sides of the object's hierarchy.

Hierarchy

Though hierarchical approach may be considered as a logical completion of the historical line from the structural methodology to the system paradigm, the notion of hierarchy is much older, ascending to the mythological cosmology of the primitive societies. The first manifestation of hierarchy is the presence of several qualitatively different levels with a kind of vertical order, when one level may dominate over another, so that the relations between the levels are of a kind other than the relations inside each level. Up to the recent time, the origin of this order was unknown — and hence hierarchy seemed to be imposed by some supreme force, which is reflected in the very word "hierarchy": "the sacred order". Now, it is clear that the levels of hierarchy represent the stages of its history, and that reflection (nonlinearity) is the key to any development [1].

Most generally, reflection is the interaction of the object with itself, which implies self-relation and self-transformation. At the structural level, reflection can be represented by linking an element of the structure to itself; in particular, the reflexivity of a relation l Î L means that <s, s> Î L for any element s Î S. However, this is not the only way to introduce reflection into the structural description, since an element of the structure may be linked to itself indirectly, via mediated or collateral links. The depth of indirection may be a criterion for the distinction of the different levels of the structure, when it is unfolded starting from a fixed element. Of course, the same structure may be unfolded in many such hierarchical structures.

For the system, reflection is easily associated with a cyclic process, when the system's output may change its environment, which would affect the system's input, and so on; this is the common feed-back scheme. When the part of environment that provides such feed-back is included into the system, the system acquires at least two levels, one of which corresponds to the "pure" functioning, while the other accounts for "self-regulation", like in the usual operation analysis [13,ch.4]. The system thus becomes hierarchical.

Since any hierarchy can only manifest itself through the variety of its hierarchical structures and systems, there may often be a lack of awareness of the hierarchy itself. The different structural and systemic description then seem uncorrelated and even controversial, and there may be hot argument between their adepts, claiming their own attitude the only truth. However, these contradictions are most likely to be merely apparent, being the aspects of the integral description [17].

The basic features of hierarchy might be summarized as follows:

• Hierarchy can be unfolded into numerous hierarchical structures, and its external behavior is, at any instance, that of a hierarchical system.

• There are no rigid levels of hierarchy, but rather hierarchy is characterized by infinite divisibility. Thus, the relations between any two levels of hierarchy constitute a specific entity which may be considered as a level of the same hierarchy lying between the two original levels. Therefore, there is no "complete" structure of the hierarchy, since one can always find a new level between any two previously discovered.

• The collection of intermediate levels between any two levels of hierarchy may be folded into their direct connection, so that the total number of levels would be diminished. The different ways of folding and unfolding the hierarchy lead to its various manifestations, or refoldings.

• Because of refoldability, there is no absolute "topmost level" in the hierarchy, though any hierarchical structure would possess one. Any element of hierarchy may become its top unit, thus representing the hierarchy as a whole.

• Hierarchy is not a simple ordering of levels, but rather a multidimensional formation. The number of its dimensions is as infinite, as the number of levels. However, each unfolding implies a one-dimensional ordering of levels, and the levels may be characterized by a definite dimension.

• Within hierarchy, the distinction between the elements and their connections may only refer to a single unfolding, thus being relative. In the same way, any functional decomposition is related to a definite hierarchical system, based on the respective unfolding of the hierarchy.

• There is a kind of self-conformity in the hierarchy. Any component of hierarchy is a hierarchy too, and it may be unfolded in the same way as the whole hierarchy. The very distinction between the part and the whole becomes relative, since every single element of hierarchy reflects it all, contains it within, thus being equivalent to it.

The "own" hierarchy of any object is another side of the hierarchy of its environment. Reflexive interaction with the environment leads to the object's development. Since refoldability assumes many ways of interfacing the external world, development may follow different routes, and different unfoldings of a hierarchy indicate the possible ways of its development. Being the unity of the internal and the external, hierarchy assumes two directions of development: it may either "zoom in" unfolding its elements and their connections — or it may grow through joining several hierarchies in one. These acts of integration and differentiation change the organization of hierarchy.

Like with the indirect links in the structure, or the processes at the systemic level, the interactions of the objects in the world may be mediated by other objects, up to the most distant influences. The integrity hence arising unites the objects with their environment, making the whole world a unity. However, this unity should be treated hierarchically, and it cannot be comprehended as a given entity, or a process — again, it is a synthesis of the both.

The object's interaction with the world may be represented by the cycle of alternating phases (levels) of action and being acted upon. The object is reproduced in each cycle, though in another state. The simplest case of such reproduction is hierarchical refolding, leaving the object the same and merely changing its "form", or its "position" in the world. One more possibility is extensive reproduction, or expansion, when a larger part of the world becomes involved in the object's environment, while the character of interaction remains generally unchanged. The next level is intensive reproduction, or development proper, which implies a shift of the boundary between the object and its surroundings, the change in the very notion of the internal. Evidently, this means a synthesis with some other hierarchy, formerly attributed to the external world.

One cycle of the object's self-reproduction provides a natural measure of time, associated with this particular development. Such time should be considered as hierarchy, since the cycle of reproduction looks differently at different levels of hierarchy, thus defining different time "scales". It differs from the time variable known in physical sciences, where it is a structural parameter rather than a measure of the level of development, hierarchical complexity. The hierarchical notion of time reflects its intuitive features, such as directedness from the past to the future, the existence of a finite "now" within each reflection cycle, and the difference in the "natural" time flow for the objects of different type.

Conclusions

The hierarchy of integrity discussed in this paper may be unfolded in different ways. One of them has lead to the hierarchical understanding of complexity, which could become a framework for further qualitative and quantitative specifications. Like structure, or system, the category of hierarchy is universal, so that any object can be treated hierarchically. All the hierarchies are identical in their organization, and may be considered the unfoldings of the same hierarchy, the different sides of the same world. This may pose many delicate questions concerning the correspondence between natural or artificial hierarchies. Thus, ideal links may become quite material bonds, directedness of development may assume the form of purposefulness, the abstractions of scientific analysis and synthesis may transform into practical development as destruction and reconstruction. One could further unfold the hierarchy of complexity, to cover the categories like "collection", "arrangement", "compound" or "mixture". Another direction of unfolding leads to such characteristics as "balance", "stationarity", "stability", "robustness" etc. One of the most important areas of hierarchical study is the investigation of different levels of mediation: passive, random mediation is typical for the inorganic world, while the organic level is characterized by active, or forced mediation, and the level of subjectivity is marked by the universal and arbitrary mediation, when any two objects become interrelated due to the projection of the world into the mind. [comment]

References

1. E. N. Yeliseyev (1983), The structure of the development of complex systems (Leningrad: Nauka)
2. M. D. Mesarovic, D. Macko, and Y. Takahara (1970), Theory of hierarchical multilevel systems (New York, London: Academic Press)
3. V. N. Sadovsky (1974), The foundations of general systems theory (Moscow: Nauka)
4. N. Cutland (1980), Computability: An introduction to recursive function theory (Cambridge, London, New York, New Rochelle, Melbourne, Sydney: Cambridge Univ. Press)
5. C. Cooper (1994), "Complexity in C3I systems", Complexity International, vol. 4;
   online: http://www.csu.edu.au/ci/vol1/Clive.Cooper/paper.html
6. A. Lerner (1967), The principles of cybernetics (Moscow: Nauka)
7. I. Prigogine (1980), From being to becoming: time and complexity in the physical sciences (San Francisco: W.H.Freeman)
8. L. von Bertalanffy (1962), "General systems theory — A critical review", General Systems, vol. VII, pp.1–20
9. R. Goldblatt (1979), Topoi. The categorial analysis of logic (Amsterdam, New York, Oxford: North-Holland)
10. L. Zadeh (1973), The concept of a linguistic variable and its application to approximate reasoning (New York: Elsevier)
11. A. Kaufmann (1977), Introduction a la théorie des sous-ensembles flous (Paris, New York, Barcelone, Milan: Masson)
12. H. M. Hubey (1996), "Special classes of fuzzy truth valuations and probability theory";
    online: http://www.csam.montclair.edu/~hubey/papers.html
13. N. Wiener (1961), Cybernetics or Control and communication in the animal and the machine (New York, London: MIT Press, Wiley)
14. M. D. Mesarovic and Y. Takahara (1975), General systems theory: mathematical foundations (New York, San Francisco, London: Academic Press)
15. P. B. Ivanov (1996), "Computability in developing systems";
    online: http://unism.narod.ru/arc/c96/c96.htm
16. M.Mesarovic (1968), "General systems theory and its mathematical foundations" IEEE Transactions on Systems Science and Cybernetics, vol. SSC-4
17. H. M. Hubey (1996), "Intelligence, regression, multiplicativity, path integrals, and stochastic models of scaling and evolution";
    online: http://www.csam.montclair.edu/~hubey/papers.html