Refoldability of HierarchiesThis remarkable feature is very important to distinguish hierarchy from mere hierarchical structure - the categories that are often confused in the literature. Though hierarchical structures are normally representations of hierarchies, one can formally construct hierarchical structures that have nothing to do with hierarchies, arranging arbitrarily picked things or ideas in an arbitrary way. The elements of a hierarchy are never arbitrary, they have become the parts of the whole in a process of development, following the objective law. A hierarchy is a strongly connected formation, in which any element is connected to any other. However, connections between different elements are different, and the very distinction between the elements and links is relative. Refoldability allows reconnection of the elements of hierarchy in any order; however, this implies a change in the quality of their connections. To grasp the idea of refoldability, imagine a crumpled net lying on the floor in a heap. If you pull one of the nodes, it will drag out the nodes immediately connected to it, and they will, in their turn, take out the nodes connected to them, and so on. In the end, you will have the net hanging down from the node you hold, with each node at its own height above the floor. You have produced a hierarchical structure. If you start with a different node, the result will be essentially the same, but the nodes will hang at some other distances from the floor, in a different order. Thus, varying the initial (topmost) element of the hierarchy, you produce different hierarchical structures. Similarly, dragging up a point of a horizontal cord, you obtain a hierarchical structure ordering the points of the cord by their distance from the flat surface:
Dragging up a different point, you obtain a different ordering of the points:
This new hierarchical structure is called another turn of the hierarchy. To understand, why the idea of rotation is invoked, consider another example. In the simplest hierarchy, there are two elements and one link between them. The two possible turns of such trivial hierarchy can be pictured as
Note that the link from A to B is of a kind different from the link from B to A, which is stressed by the notation. The example of a triadic hierarchy gives even stronger impression of rotation:
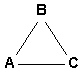
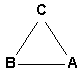
Of course, such simple examples do not convey the whole complexity of hierarchical refolding. However, they illustrate how a hierarchically organized thing can turn its different aspects to the world, both changing and remaining the same. The examples with the net and the rope also demonstrate yet another important feature of refolding: to get to a specific turn of the hierarchy, it must be first folded to some neutral state, and then unfolded, starting from a single element that represents the hierarchy in this particular unfolding (hierarchical structure). In the discrete case these two operations are not as obvious, but they still have to be involved. Unfolding hierarchies The logic of unfolding is based on the relativity of distinction between the elements and links. Thus, in the scheme A ® B, the link ® can be considered as an element M mediating the connection of A to B: A ® M ® B. As a result, one obtains three levels of hierarchy instead of original two. Any link between the neighboring levels can thus be represented by an intermediate level, and the hierarchy can be unfolded again and again. This is one of the infinities characteristic of any hierarchy. Once again, it should be stressed that the quality of links between the elements and levels in any hierarchical structure depends on the process of unfolding, and similar structures may represent quite different turns of hierarchy. This can be often observed in modern mathematics, where the same notions (e.g. a set) can be introduced in the contest of very different conceptualizations (like number theory or the categorial approach), with all the properties preserved, but in a different sense. Sometimes, this difference can become apparent, like in the case of Riemann and Lebesgue integrals, which coincide in non-singular domain, but can lead to different results for singular integrands. Unfolding of hierarchies is quite common in our everyday life. Thus, when we first meet somebody, we usually pay attention to some particular details of the person's appearance or behavior, and our further acquaintance with that individual proceeds through extension and moderation of this primary impression. Also, we split a large project into relatively separate stages, which can be split into even smaller subtasks. In nature, unfolding is often associated with a fluctuation, a violation of symmetry, or "bifurcation" (in the sense of the catastrophe theory). In any case, this is a natural process, co-relating a thing with its environment. Folding hierarchies The inverse logic of folding treats every indirect (mediated) link A ® M ® B as a direct link of a different type: A Þ B. Intuitively, this corresponds to the common reasoning that, if two things are related through some other thing, they are related. The focus shifts from the mediation of connection (its mechanism) to connection itself, since, in many applications, we do not need to know about the details, as soon as we get the overall result. Folding is a transition from one hierarchical structure to another structure, which is simpler than original in certain respects. In our everyday life, we have a typical example of learning, when a complex action is first performed operation by operation, but it gradually folds into a single operation that does not require conscious control of the intermediate steps. In principle, a hierarchy can be folded to a single element, but it of more common, when the process of folding stops at some level, with further unfolding in another direction. The neutral state, to which the hierarchy becomes folded can therefore be complex enough, and there can be a hierarchy of such neutral states. Multidimensional structures Any element or link in the hierarchy is a hierarchy on itself, and it can be unfolded in its own way, regardless of the current turn of the parent hierarchy. Thus, the scheme A Þ B could become something like
However, since any part of the hierarchy is connected to any other part, one has to indicate how the missing links, which can be done in many ways. For instance, one could consider parallel unfolding of each of the primary levels:
However, quite often, different levels will unfold themselves following their own ways, and the hierarchical structure of the lower level will be represented by one of the higher level elements, while the rest is only indirectly related to the lower level development:
Obviously, the number of dimensions in any hierarchy can grow to infinity, and all such possible unfoldings (turns) are determined by the hierarchy as a whole and, in that sense, contained in it. Any thing at every moment is in infinitely many relations with the world, in every one of which it is represented by a specific hierarchical structure. In human activity, all that infinity is handled using the same property of refoldability, applied to the hierarchy of admissible rotations of hierarchy: we see a particular turn (the topmost element), with the rest serving to enrich it with inner complexity.
[Unism & Philosophy] [Unism] [Main sections] [Page index] [Keyword index] [Search] [Contact information] [Guestbook] |


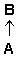

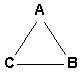
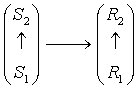 .
.
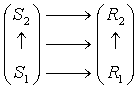 .
.
