Antes de emprender la lectura de este parágrafo, conviene que el lector experimente con
* un OCR (optical character recognizer) como el que usan los escaners de lectura de textos, de los cuales es muy did'actico el programado por The Visible Neural Network, Inc, denominado Optical Character Recognition Demo, del cual el principal mensaje resulta ser que con cada ciclo de entrenamiento que pasa, el OCR va acertando un número creciente de patrones que en realidad son letras mayúsculas y dígitos, evidencia que aprende; y
* algun simulador tipo robot bidimensional, de la conducta de un invertebrado o de un batracio, entre los cuales es muy recomendable el programado por Beer y ofrecido con el nombre de Nervous System Construction Kit para PC, por los Williams, del cual el principal mensaje es que cambiando los parámetros de algunas de las casi 80 "neuronas" computacionales, similares cada una de ellas a las dos que se grafican en b de la Fig 17, cambia la conducta del robot bidimensional. El robot opera como un conjunto autoorganizado del cual se observa en el monitor cómo se desplaza, cómo retrocede en callejones sin salida y como bordea obstáculos que lo separan de la fuente de bioenergía, mostrando transiciones de fase del desequilibrio cuando enfrenta obstáculos preparados por el estudioso o cuando detecta dicha comida y se harta de ella. En este caso La inteligencia del robot no requiere memoria y se basa en la adaptabilidad del circuíto neural a las condiciones externas. En ese circuíto no existe un agente que dirija el tráfico ni un reglamento innato que rija la conducta: la principal explicación reside en la tendencia termodinámica hacia un espontáneo y cambiente equilibrio de Kirchoff, que oculta el respeto al principio de Le Chatelier.
En el primer caso el diseño se parece a la Fig 19, cuyo texto es un resumen de lo que se puede observar con el ORC.
En el segundo caso se está empleando el bastante reciente acierto de Hopfield (1982) con el reemplazo de las neuronas biológicas por amplificadores operacionales analógicos, diseño que alcanza, en principio, para explicar muchas propiedades trascendentes del cerebro humano a nivel subsimbólico y subcognitivo, sobre todo algunas de la memoria asociativa y de la interpretación de la información. Los amplificadores operacionales analógicos, las resistencias, los condensadores y el cableado de Hopfield son dispositivos electrónicos, aptos - como es el caso - para ser simulados con programas computacionales digitales. La computación colectiva que allí se logra se basa en
* partir de condiciones iniciales alejadas del equilibrio y que representan un problema físico a resolver a nivel subsimbólico, de interpretación de la información y de memoria asociativa; y
[53]
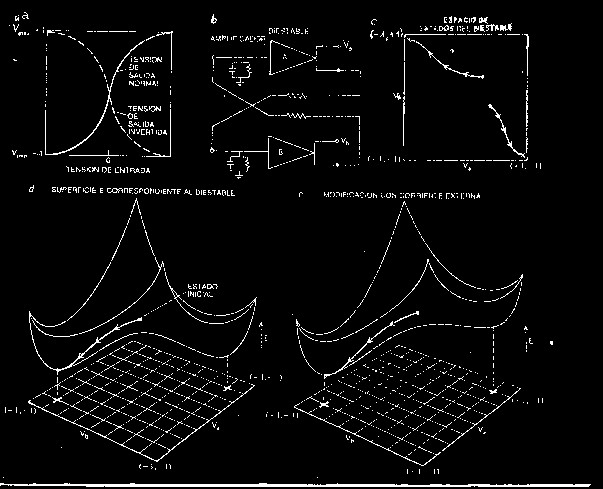
Fig 17.- Circuíto biestable o flip flop, con tomas a tierra batería - resistencia para cada uno de los dos amplificadores operacionales. El amplificador simula a una neurona y la toma a tierra simula a la membrana de la neurona, por la cual se pierde actividad. (a) Cada amplificador operacional de (b) se puede saturar con valores límite o asintóticos cualquiera que sea la tensión de entrada de alguna de las dos maneras indicadas por linea llena (normal, excitatriz) o de rayas (invertida, inhibitoria). Esta última se usa en el ejemplo. (b) La evolución del circuíto biestable depende del cociente entre los pesos de las resistencias centrales. Los dos circulitos blancos Va y Vb son los sitios para introducir las excitaciones externas o inputs. Los otros dos a la izquierda son posiciones adicionales para el ingreso de corrientes. Los dos llenos o negros son sitios usados para la medición de los potenciales Va y Vb de output registrados en las graficas siguientes. (c) Si el proceso recibiese Va = Vb a la entrada y tuviese iguales valores para las dos resistencias centrales de (b), evolucionaría ya sea hacia (Va Vb) valiendo (-1 +1) o bien a (+1 -1), los dos atractores existentes. La trayectoria superior comienza con Va = Vb, puesto que esta sobre la diagonal que actua de separatrix (lugar geometrico separador) entre ambos atractores. Se orienta hacia uno de los atractores en lugar del otro por algun desbalance circunstancial que no aparece explicito, pudiendo ser asimismo una trayectoria hacia el otro atractor motivado por otro desbalance. La segunda [54] trayectoria marcada se explica porque el punto inicial está del mismo lado de la separatrix que el atractor. (d) Trayectoria en el caso cuando las resistencias centrales de (b) son iguales. (e) Lo mismo, pero aquí desiguales: desaparece la biestabilidad y pasa a haber un atractor único asimétrico con rotura de la simetría previa. De un ordenamiento inicial biestable (d) hubo una transición de fase hacia otro ordenamiento distinto monoestable (e) causado por el cambio desde un cociente entre los pesos de las resistencias centrales con valor, por ejemplo, 1, hacia otros valores apartados. (Tank y Hopfield, Investigación y Ciencia, feb 1988, p. 47).
El signo o voto s ingresa en una fórmula que contabiliza todas las interacciones de ida y de vuelta de todos los amplificadores operacionales (neuronas) de la red. Ella es, justamente, la fórmula para la energía E a minimizar, energía análoga a la que aparece al alterar los espines del vidrio de espin y que se ha denominado energía de cómputo:
E = -(Sigma) Vij. si.sj => MIN (5)
iØj
energía que evoluciona hasta que todos los signos si(t) de los
amplificadores coincidan con este otro signo:
sgn (Sigma) {Vij(sj(t))+1]/2 - Voi } (5a)
En el caso infrecuente de obtenerse cero con esta expresión, convencionalmente se reemplaza dicho cero por +1.
V es el potencial, la actividad o el estímulo para la descarga
i es el sumidero
j es la fuente
o se refiere al valor umbral necesario para que se produzca descarga
sgn indica el signo.
La expresión (5a) contabiliza el signo que surge de contrastar un minuendo - el estimulo actual - y de un sustraendo - el estímulo umbral - y modificando el -1 de la nomenclatura de (5) por el cero en la nueva de (5a). Para s hay dos valores, +1 y -1; para el minuendo de (5a) esos dos valores son +Vij y cero. Todos los signos pueden ser positivos al final, o bien todos negativos. En cualquiera de ambos casos la energía de cómputo es mínima y el proceso termina. Mientras no coincidan los signos, el proceso sigue. A su vez, la expresión (5) invita a maximizar los diferentes Vij y a lograr que no haya diferencia de voto entre i y j. Como ejemplo considérese el circuíto biestable con N=2 amplificadores saturables de la Fig 17.
Cualquiera que sea la zona de partida para las dos V posibles, convergen a que si la salida de Va tiene un signo, la de Vb tiene el opuesto, con lo cual se presentan dos atractores posibles. Corresponden a equilibrios de Kirchhoff, estables frente a pequeñas perturbaciones. La dinámica se
[55]
Fig 18. En este modelo esquemático de las neuronas fotorreceptoras del caracol, las zonas punteadas son modificaciones anatómicas resultantes de un aprendizaje antihebbiano (Daniel Alkon, Sci. Am., 261,1 (July 1989).
estabiliza con mínima energía de cómputo de la ec. (5) sujeto a la restricción (5a). Esto exige una actualización asincrónica de los N amplificadores, ya que fracasa con actualización sincrónica.
En 1982 este desarrollo significó una gran novedad. Las redes con esta arquitectura pueden aprender. Cómo aprenden depende de muchos factores. Observando el robot bidimensional de Beer citado al principio de este parágrafo, el circuíto no aprende de manera alguna y corresponde a la situación ideal "x" en el orígen de coordenadas de la Fig 9. Observando la operación del OCR, el circuíto realmente aprende en la medida que los datos analizados a la entrada tengan estructura. Pueden encontrar relaciones en común de muestras a la entrada que se les proporcionan (aunque no es nada sencillo traducir esas relaciones, que usan muy bien las redes, a significados fáciles de entender) y generalizar esas mismas relaciones a otras situaciones, como hacen muchos robots y animalitos (Apéndice 4).
6.dic.2000
Pulsar tecla de vuelta
Vuelta a índice de Biotermodinámica del Cerebro
Raúl Barral - Carlos von der Becke: Biotermodinámica del Cerebro - 2000
