 podas alfa - beta
podas alfa - beta
.
Definición: Tanto una - la poda alfa - como la otra - la poda beta - son métodos para limitar la búsqueda en los árboles de búsqueda del algoritmo MiniMax, basados en considerar racionalmente que es inútil explorar la totalidad de la estructura del árbol decisional, porque ni a "mí" ni a "mi contrincante" nos va a convenir introducirnos en algunas de las ramificaciones, pues están dominadas ya sea para mí (poda alfa), ya sea para el contrincante (poda beta).
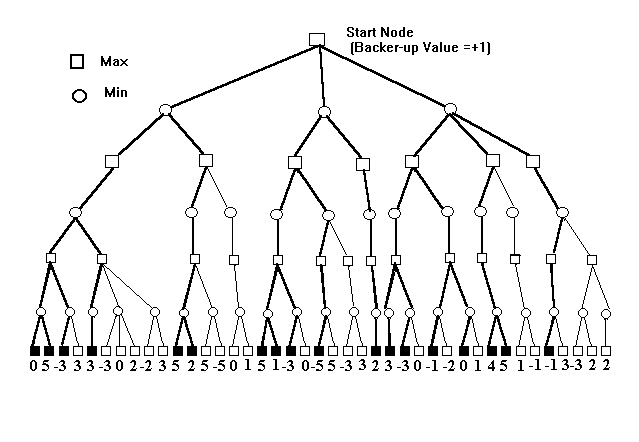
Sea el árbol de búsqueda donde se ha estudiado anteriormente la función de evaluación y sus resultados aparecen transcriptos en el séptimo nivel. Sin saber esas cifras, le toca decidir al jugador maximizante cuál jugada le es óptima (qué cifra ubicar en el cuadrado del primer nivel).
Estudiaremos la poda más sencilla de este árbol. Busque el lector en el séptimo nivel la secuencia 3,-3 y 0 (cerca del centro, no confundir con otra que está a la izquierda) y anótela en un papel, con los círculos y cuadrados de más arriba enlazados con 3,-3 y 0.. Hay que llenar los dos círculos MIN del sexto nivel relacionados con dichas tres cifras. En el primer círculo lo único que cabe es ese "3". Ese "3" es un candidato a ser seleccionado por MAX (el cuadrado en blanco del quinto nivel). Veamos cual es el otro candidato. Durante una búsqueda primero en profundidad desde el quinto nivel MAX halla un "-3" que le encantaría a MIN. Para evitar la "tentación" de MIN eligiendo ese buen valor, MAX pierde todo interés en esa rama y no la elige: lo hace con "3" (dominante) en lugar del "-3" (dominado). Ha podado por poda alfa la ramita entre el círculo con "3" y el cuadrado con 0. Podar es sinónimo de omitir el cálculo que da 0. Obsérvese que en el mapa ese camino se dibujó pálido y el cuadrado de 0 se ha dejado vacío. Entendiendo este ejemplito, el lector puede reconocer 5 podas alfa más entre el sexto y el séptimo nivel.
Ahora una novedad. Se llaman podas beta las que decide MIN. Por ejemplo MIN (ubicado en los diferentes nodos circulares del cuarto nivel) no tiene interés en favorecer a MAX y poda tres ramas a la izquierda, entre el quinto y el séptimo nivel, cuando encuentra una primera evidencia de su irrelevancia para sus intereses. Ubicado MAX en el tercer nivel.elegirá podar por poda alfa la rama que acaba en -3 y 3 - así como otra rama que acaba en -3,2,2. Desde el segundo nivel habrá dos podas beta adicionales. Total el esfuerzo de cálculo se reduce fuertemente. Obsérvese que la poda es función del orden arbitrario en que se ubican los nodos superiores. La secuencia ganadora es la que contiene un 2 en cada nivel (casi al centro). Si por casualidad empezamos por la secuencia ganadora, la poda es bastante mayor. O sea que la eficiencia de la poda es función del orden de procesamiento de los nodos por una búsqueda primero en profundidad.
19.may.2000
Pulsar tecla de vuelta
Glosario de Bioingeniería del Conocimiento - Carlos von der Becke.