Hexagons in a close-packed world. Hexagons Forever!

HEXAGONS in a packed World

GONSHEXAGONS HEXAGONSHEXA GONSHEXAGONS HEXAGONSHEXA GONSHEXAGONS	Hexagons are everywhere!. Everywhere you can find a bunch of homogeneous objects that is. Whether we look into beehives, man-made devices, living tissues or even atoms we can find surprising examples of a characteristic hexagonal pattern. We call it hexagonal close packing and it is in fact most effective to pack the largest number of objects in a minimum space. Let us see some examples.
Each of the hexagonal cells on the right shows an example of hexagonal pattern. Some are natural, some man-made. Keep reading and you will run into many surprises, as well as enlightening similarities and differences. I would suggest following the numbered sequence, beginning with the familiar beehive honeybee pattern below(1).

1

honeycomb beehive ¿ Have you ever wondered why bees make their beehives in their characteristic honeybee pattern?. As you know, each cell will harbor one larva on its way to become a bee. As we will see, the typical "honeycomb" hexagonal arrangement is the most efficient way to pack as many cells as possible in a limited space.
By the way, did you know that bees make each cell cylindrical, like a tube?. The fact that the cells look hexagonal is due to their compression by the six closest neighbors in the crowded colony!.

It is something similar to what happens to bubbles when they get together. Isolated bubbles are spherical but look how they look like when they stick together. foam

2

solar panel We humans have also managed to figure out how to pack disks, cylinders or spheres efficiently. Those on the left are single-crystal Silicon wafers (thin disks) arranged in a photoconversion panel for harvesting solar energy. Again efficient hexagonal packing.

3

We are able to close-pack disks in two dimensions and also spheres in three dimensions. Piles of fruit are a tasty example. Each layer of oranges in this pile is close-packed as the silicon disks above. As we move up we put each new orange sitting on the middle point between three bottom oranges, and... we end up with hexagonal close packing along the vertical direction too!. Try it at home. If you don't have oranges cannonballs will also do : ) Could you guess how many oranges would be directly in contact with an orange inside this pile?

4

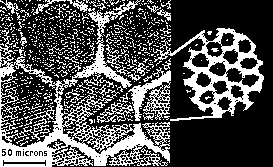Nb superconductor So far we have seen examples of hexagonal arrangements of macroscopic objects. But the microscopic world is also full of interesting examples. The image on the left is a micrograph of a cut of a superconducting cable. This cable is made of many fibers wich in turn are made of many tinier filaments (seen as small dots). The scale on the bottom marks the size of 50 microns (1 micron is 1/1000 millimeters), so that a 0.5 mm thick cable would span almost a full (14") screen. The larger fibers, with radius of aproximately 50 microns pack together very much like cells in a beehive. In this case the fibers were also little cylinders to begin with. But the process of fabricating the cable, by forcing it to pass through a series of size-reducing funnels forces the fibers against each other and the familiar honeycomb pattern results. Now, if we look closer inside each fiber we can see even smaller filaments each made of superconducting niobium which have also SPONTANEOUSLY packed into a close-packed hexagonal array !.
That is the way in which a given number of filaments can get to occupy the smallest space.
If we take a bunch of straws, as in the picture on the right, or pencils or toothpicks, and hold them tightly together with a rubber band that is precisely what we get: hexagonal close packing.

5

Up to this point we have seen a few examples of human-made (also bee-made) close-packed structures. It might seem that these arrays are a signature of intelligence (we could always think that bees are pretty inteligent too, after all they are even able to orient themselves and comunicate directions!).
Yet, we will soon see amazing examples of hexagonal packing in unsuspected places that will rule out this self-indulging hypothesis.
fovea spots This picture represents a section of a sensitive part of the retina called the fovea ("Yellow Spot"). The fovea is a small (less than 1 square mm) but very specialized region of the retina. There the sampling of light is at its finest. It consists of discrete cellular elements: very thin (3 µm) elongated cone photoreceptors (rod-shaped but seen here as black spots). The mosaic of foveal cones is highly condensed (200.000 cones/sq.mm in the adult human ) providing maximum
resolution of space, contrast and color. And how are these rod-cells arranged ?. You got it !.
They cover the space most efficiently adopting a hexagonal (honeycomb) pattern (take a stack of round toothpicks for example and look at their tips). In this case we find the pattern at the cellular level. These are truly self-assembled complex tissues.
To finish this section, here is a cute similarity between natural and man-made devices: Photosensitive panels used in man-made night vision devices are also built with close-paked hexagonal arrays

6

CIMA reaction spots     If you thought self-assembly of cells was amazing wait until you read the next one.
After all, cells can assemble according to preordained instructions coded in DNA, right?. Nothing to it.
    But what if I tell you that certain chemical reactions, kept far from their thermodynamic equilibrium, can evolve into ordered heterogeneous sytems with hexagonal symmetry ?. It would be as amazing as pouring ink into water and eventually getting a spotty mixture !. Well, something like that is what happens in the case of the figure on the left. A reaction in a continuously fed reactor between chlorite and iodide in the presence of malonic acid (CIMA reaction for short) can go back and forth. Coupled with molecular diffusion and evolving far from equilibrium, this reversible reaction leads to iodide-rich (blue) and iodide-poor (yellow) regions which ORDER SPONTANEOUSLY into our already familiar hexagonal symmetry.
   And these funny chemical reactions are full of other surprises. The hexagonal pattern is the most stable of the two, but only small variations in the concentration of reagents in the same CIMA CIMA reaction stripes reaction, in the same reactor, can lead to the radically different pattern on the right.
Aren't these patterns awfully familiar ?. We can certainly found them in Nature, here and there. I will put some relevant pictures here as samples but probably you could find some more. (Point to each one to find out their true nature).
cheetah spots fish skin fingerprint inside a human cell zebra stripes
Probably more than amazing similarities. Don't you think?

7

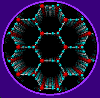
   And now... we will get into the atomic realm.
   Yes, there too we will find hexagonal close-packing. As a matter of fact it is a classical example.
    If we consider atoms as single spheres then there is no surprise that when many of them get together (for example in metals at room temperature or certain gases at very low temperature) they arrange as shown in this figure. Not only neutral atoms pack in this way. Ions (charged atoms) also do, as long as their charge could be effectively neutralized by other ions of opposite charge sitting in some of the intersticial sites of the structure (small triangular cavities in the figure).
hexagonal close-packed array of atoms    And how do we know that they arrange themselves like that?. Atoms are so small that they cannot be seen with microscopes (although High-Resolution Electron Microscopes are getting close to it). But scientists devised a trick to "see" atoms and molecules in crystals by shining X-rays onto them and measuring the rays reflected by the crystal in each direction of space. This is X-ray crystallography, amounts to what we could call "X-ray vision" and lets us know that indeed in many elements, atoms are arranged as shown here but in the three dimensions of space. That is something like in the pile of oranges shown above, in section 3.

8

   After all these examples it looks as if close packing could be found anywhere!. Well, almost anywhere. But not quite; you need crowding of similar homogeneous objects, whether atoms, cells or oranges. We do not find this packing in stars or galaxies, far away from each other. But certainly in our packed world it is possible to find this recurrent pattern in many different places and at many different scales.
   Since ours is a complex world, not always things will be as straighforward as the examples shown here. Let me show you some of the exceptions, complications and variability that we can find in Nature.

   Sometimes we can find perfectly hexagonal patterns which are not the result of close packing.

    Ice crystals in snow flakes for instance are always hexagonal and this geometry can be traced back to the arrangement of the molecules of water frozen into a hexagonal structure (See the related story Snow flakes). But this symmetry is the result of the geometry imposed by the chemical bonds in the lattice of ice. It is the atoms making the crystal and how they "like" to bond to each other that determine the hexagonal arrangement in this case.
   Something similar happens in the case of graphite, a black form of carbon used as a powder in the core of pencils. Graphite has hexagonal symmetry that derives from the way each Carbon atom shares electrons through chemical bonds with three nearest neighbors (See the story Is this a molecule?).

Sometimes we can find close packing not leading to perfectly hexagonal arrays.
   And this is so because real systems are not always as ideal as balls in a pool table. In order to have hexagonal close packing we need isotropic objects all of the same size. If the sizes are different funny things happen. As in the buble bath below. There we can find medium-size bubbles surrounded by six other bubbles. But there is also a smaller sized bubble surrounded by five neighbors. A larger than average bubble would be obviously surrounded by more smaller friends.

The other two pictures next to the bubble bath represent examples of natural and man-made systems where we can find patterns with complexities similar to that of foam. The middle pictures are different views of a plastic very familiar to all of us in the form of expanded polystyrene foam (styrofoam, the white light stuff used in packaging). This material is made by soaking polystyrene beads with a solvent of low boiling point (pentane) then heating quickly so that the solvent is boiled out, the plasric beads expand, growing into each other and becoming at the same time less dense (more volume for the same weight). If all the expanded beads were the same size then perfect packing could be expected. Since there is enough dispersion of sizes we get a situation similar to the bubble bath. After all it is a foam.
The final image is a micrograph of cork. Also a light-weight material, but in this case one found in nature. Cork is so light because it is full of air. It is formed by long empty channels that run perpendicular to the picture. Again, these channels are densely packed but their different sizes and irregularities make the pattern less obvious.

Sooo... we run out of examples of closed-packed hexagonal systems. Or didn't we?.
Not quite actually.
I will show you now a few more examples and I invite you to let me know of any other you can think of. I'll include it in the list!

This leopard-like pattern shows the distribution of lines of a magnetic field when they begin to penetrate a superconducting sample. The position of the lines can be calculated according to models and also detected experimentally by "decoration" with magnetic particles. In both cases it is shown that the lines (in the picture cut as brown dots) pack with approximate hexagonal symmetry

This is a close-up fotograph of the speakers in my computer. By paking holes as densely as possible in these grids, dessigners kill two birds with a stone: as much open space to let sound go through and the smallest amount of material (in this case plastic) to make the grid. Can you think of any other "net" with these characteristics. Used in farms maybe?

Chicken wire, yes.
The End

Send your comments or examples of other hexagonal packings to science4all@iname.com

Back to main page on Science Technology and Society