The three components (SC, ERC, and IRC)can be determined by various approaches. Both SC and ERC can be found from the geometry of the visible sky or external reflected surfaces, whereas based on inter-reflected theory, IRC can be found from formula, nomogram, or tables.

          DF = SC + ERC + IRC

where DF -- Daylight Factor
           SC -- Sky Component
           ERC -- Externally Reflected Component
           IRC -- Internally Reflected Component

Assessment of daylight factor:

When a building already exists the values and distribution of daylight inside the building can be measured directly. A daylight factor meter is a specially calibrated light meter (photometer) which gives direct readings of the daylight factor at any point.

The prediction of daylight factors at the design stage requires a knowledge of the proposed building and its surroundings. It is possible to calculate the three components of the daylight factor by using information about the size of the windows and room, the size of any external obstructions, and the proposed reflectances of the surfaces. The sky component is the major contributor to a daylight factor and can be considered as the percentage of an unobstructed sky that is visible from the reference point.

The following methods can be used for predicting the daylight factor in a building.

   Tables of window and room dimensions.

   Grids of the sky such as the Waldram diagram.

   Computer programs.

   Physical models measured in an artificial sky room.

   Daylight factor protractors.

The use of special tables, diagrams and protractors are techniques which help bypass the many repetitive calculations needed to predict the daylight factor at each point within a room. The Waldram diagram, for example, is a specially scaled grid representing half the hemisphere of sky. Using scaled plans of the room, the area of sky visible through the window from the reference point is plotted onto the grid. The area of grid covered by this plot is proportional to the sky component at the reference point.

Computers are easily programmed to repeatedly make the tedious calculations needed for the prediction of daylight factor. Modern software packages for the prediction of daylight ask you to enter the details of your room, windows and reflecting surfaces, and to specify a grid pattern within the room. After calculating the daylight factor expected at each grid point the results may be shown on screen as daylight factor contours between the points and also given as a printout.

BRE daylight factor protractors:

The special protractors developed by the Building Research Establishment are widely used to determine daylight factors at the design stage of a building. Protractors are available for glazing set different angles and for either a uniform sky or a CIE sky.

A daylight protractor , as shown in Figure 6.1, contains two semi-circular scales on transparent overlays, which are used with scale drawings of the room being assessed. The primary scale measures the initial sky component and an auxiliary scale makes a correction for the width of the windows. The protractor also contains an ordinary scale of angle used to find the angle of elevation of the patch of sky being assessed.

                          
Fig. 6.1 BRE Daylight Protractor on section drawing

Calculation of sky component

Step 1
    Take  a section and a plan drawing of the room, drawn to any scale. Mark reference
     points on the drawings, usually a regular grid of points at working plan height.
     Choose  a protractor that is suitable for the angle of glazing and for the type of sky
      required.

  Step 2
      On the section draw sight lines from the chosen reference point to the top and
      bottom  edges of sky visible from that point. Place the primary scale of the protractor
      over the section, aligned on the reference point, and read the two values of the sight
      lines, as shown in Figure 6.1. Subtract the two readings to obtain the initial
      uncorrected value  of sky component.

    Step 3
        Use the normal protractor scale to read the angles of the sight lines and average
        these readings to obtain the mean angle of elevation of the sky.

      Step 4
         On the plan draw sight lines from the same reference point to the vertical edges of
         the sky visible from that point . Place the auxiliary scale of the protractor over the
         plan, aligned on the reference point as shown  in Figure 6.2. Use the average
         scale of elevation to select the appropriate semi-circular scale and read the values
         of the sight lines. To get a final correction factor add these readings if they are on
         opposite sides of the vertical; subtract the readings if they are both on the same
         side.

                                  
Fig. 6.2 BRE Daylight Protractor on plan drawing

         Step 5
            The sky component for that point is equal to the initial value found in step 2
             multiplied by the correction factor found in step 4.

                                   
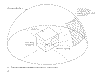
Fig. 6.3 Principles od daylight penetration directly from sky through window

Tables

Table 1 is used for determining the sky components for windows with clear, vertical, rectangular glazing in conjunction with a CIE standard overcast sky. Other tables are available for other forms of glazing, e.g. roof lights.

The procedure for a measurement position on the line of window and at sill level (Fig. 12.1) is as follows:

                                  
Fig. 12.1 A window with the sill on the working plane, and the reference point on the centre line of the window.

1. Establish h₁, the window head height above the work plane level,
2. Establish d, the distance from the window to the point considered,
3. Express d as a multiple of h₁ (i.e. the h₁ /d ratio0 and locate this at the right hand column of the table (ratio H/D),
4. Establish w₁ and w₂ , i.e. the width of window to either side of the perpendicular (w₁+ w₂ = total width),
5. Express both widths as a multiple of d (i.e. ratios w₁/d and w₂/d ) and locate these in the bottom row of the table (ratio W/D),
6. Read the two values in the table. The sky component for the point considered is the sum of the two values.

For a position off the line of the window, the sky component can be obtained by evaluating sky components for a series of windows and obtaining the required sky component by a process of subtraction and addition, see Figure 12.2.

                               
Table 1 Sky Component SC (CIE) standard overcast sky for vertical glazed rectangular windows

                               
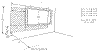
Fig. 12.2 A window with the a high sill , and the reference point outside the width of the window


Calculation of externally reflected component