HOOFDSDTUK 6: BETA-ATTRACTOREN IN DE (ZELF)ORGANISERENDE STROOM

HOOFDSTUK 6

Beta-attractoren in de (zelf)organiserende stroom

Tot nu toe hebben we aangetoond dat er twee types processen bestaan.

Ten eerste zijn er de spontane processen van "niet geïnformeerde entiteiten". In afwezigheid van informatie zal een spontaan proces tot maximale verspreiding van materie, energie en informatie leiden. De typevoorbeelden van dergelijke processen zijn de verspreiding van gassen, of de verspreiding van een druppel inkt in water. De initiele symmetrie wordt hier geleidelijk aan gebroken, om te eindigen met een evenwichtssituatie met minimale symmetrie en maximale waarschijnlijkheid.
De Tweede wet van de thermodynamica geeft voor deze evolutiepatronen - waar incoherentie de hoofdrol speelt - een voorspelling van de "evolutionaire gewoontes".

Ten tweede hebben we de processen beschreven die plaats hebben onder invloed van coherente Alfa-attractoren. Deze Alfa-attractoren dempen de variaties die ontstaan ten gevolge van gewijzigde flux in de omgeving. Het gevolg is een coherent dempingspatroon. Dit dempingspatroon is in vele gevallen zo coherent, dat een relatief éénvoudige mathematische beschrijving deze "evolutionaire gewoontes" kan samenvatten (zoals bijvoorbeeld de wet van Hooke, en de wetten van Newton).

In dit hoofdstuk zullen we complexere dempingspatronen onderzoeken, die door Beta-attractoren worden gekenmerkt.
We zullen hiervoor de tweede wet van de thermodynamica moeten uitbreiden, zodat hij toepasbaar wordt op deze complexere evolutieprocessen. Bovendien zullen we het "actie leidt tot reactie-principe" van Hooke en Ne

wton moeten uitbreiden naar deze minder coherente evolutiepatronen.

We zullen dit hoofdstuk starten met een overzicht van de belangrijkste theoretische grondleggers in dit domein. Uiteindelijk zullen we de diverse "niveau’s" van Beta-attractoren trachten te onderscheiden, gaande van éénvoudige kanalisatiepatronen, via feed-back cycli tot en met de vorming van hypercycli.

Terug naar de index van dit hoofdstuk

1. DE UITGEBREIDE WETTEN VAN DE THERMODYNAMICA

De eerste en de tweede wet van de thermodynamica zijn belangrijke wetmatigheden, omdat ze de algemene tendens tot verspreiding beschrijven.
Ze zijn echter gebonden aan een belangrijke voorwaarde, die in de natuur meestal niet geldig is !

Ze gaan ervan uit dat de systemen die we bestuderen, gesloten systemen zijn, die geen energie- of materiaaluitwisseling met de omgeving hebben. De meeste systemen in de natuur zijn echter niet gesloten, omdat stromen van energie en materie doorheen het universum vloeien (cfr. het "Panta rei"-principe). De aarde is geen gesloten of geïsoleerd systeem, omdat bijvoorbeeld de zon de aarde bestookt met zonne-energie. Deze zonne-energie levert bijvoorbeeld de energie voor de weersystemen, en is uiteindelijk ook de energiebron voor de meeste levende wezens op aarde.
Om die reden kunnen we de eerste twee wetten van de thermodynamica slechts toepassen in systemen waar de in- of uitstroom van materie en energie te verwaarlozen is.

Voor andere systemen, dienen we de wetten van de thermodynamica uit te breiden. Omwille van het feit dat er in- en uitstromen zijn voor deze systemen, zegt men dat deze systemen "niet in evenwicht zijn". (Ze kunnen wel een toestand van "quasi-evenwicht" bereiken).

In 1908 toonde Carathéodory voor het eerst aan dat de "entropietoename" geen algemeen geldende beschrijving is voor de tweede wet van de thermodynamica.

Een grote doorbraak in de beschrijving van deze systemen werd gemaakt door Ilya Prigogine,
die de inzichten rond het gedrag van systemen "uit evenwicht" heeft beschreven.

Figuur H6F1 : Ilya Prigogine, kreeg als grondlegger van de niet-evenwichtsthermodynamica de Nobelprijs

Prigogine heeft hiervoor in de jaren 1970 de nobelprijs gekregen ; hij bestudeerde met zijn Brusselse onderzoeksgroep het gedrag van systemen uit evenwicht. Zijn ideeën heeft hij samengevat in verschillende boeken, waaronder het meest bekend wellicht "Orde uit chaos" is.

Bij deze evolutiepatronen "uit evenwicht" is kenmerkend dat ze enkel kunnen bestaan zolang materie en energie wordt toegevoerd van buiten het systeem. Deze systemen dienen als het ware "gevoed" te worden om te kunnen blijven bestaan.
Reeds in 1955 stelde Prigogine dat in open systemen, de entropie wordt bepaald door een interne component "dSi" en een externe component "dSe". De totale entropie van het systeem is de som van beide :

dS_(systeem) = dSe_(systeem) + dSi_(systeem)

De tweede hoofdwet van de thermodynamica blijft geldig, doch met een zeer belangrijke nuance. In systemen die niet in evenwicht zijn, kan de totale entropie binnen het systeem verlaagd of verhoogd worden, afhankelijk van de waarden van de interne en de externe component.
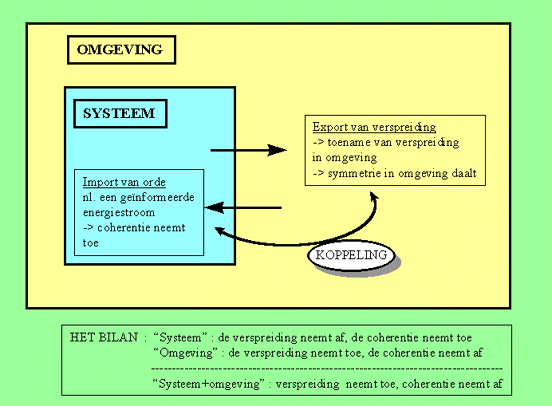
Met andere woorden, de ordening binnen in een systeem kan toenemen (dS verlaagt), op voorwaarde dat de externe component groter is dan de interne component (-dSe_(systeem) > dSi_(systeem), dan dS_(systeem) <= 0).

Als een systeem "orde" importeert (door de voedende energie en materiestroom), dan kan de wanorde binnenin het systeem afnemen (zie figuur 2). Voorwaarde is wel dat er voldoende entropie gecreeërd wordt in de omgeving : dit wordt de entropie-productie genoemd. Als er voldoende wanorde wordt gecreëerd in de omgeving, dan is het "verspreidingsbilan" van systeem + omgeving nog steeds positief, en is voldaan aan de tweede wet van de thermodynamica.

Figuur H6F2 : Een positief bilan ten gunste van de verspreiding

Dergelijke systemen, die hun interne orde handhaven door continue consumptie van materie/energie, heeft Prigogine "dissipatieve systemen" genoemd. Het uiteindelijke bilan van hun energiestroom is immers zo, dat ze energie verspreiden of dissiperen in de omgeving. (Merk op dat we ook in het vorige hoofdstuk over éénvoudige "dissipatieve elementen" hebben gesproken).

Niet-levende systemen, zoals wolken in de lucht en golven op de zee, en levende systemen zijn volledig afhankelijk van externe energieflux om hun interne organisatie te kunnen behouden. Door deze energietoevoer kunnen ze zich verwijderen van de toestand van volledige verspreiding, en kunnen ze een toestand van "quasi-evenwicht" en verhoogde coherentie behouden, buiten het evenwichtsgebied.

Morowitz heeft in 1968 aangetoond dat de flow van energie doorheen het systeem, zal leiden tot het ontwikkelen van een cyclische energie-stroom binnen het systeem. De Wet van Morowitz blijkt algemeen geldig te zijn, van quantumsystemen tot complexe levende systemen. Deze cyclische aard van dissipatieve systemen kan bijvoorbeeld gezien worden in het ontstaan van cyclische periodieke attractoren. Het ontstaan van deze cycli, zou niet alleen een bijdrage leveren tot de stabiliteit van de systemen, maar zou ook de basis vormen voor de ontwikkeling van structuur en hiërarchie binnen de systemen. We zullen in dit hoofdstuk dan ook 3 niveau’s van cycliciteit bekijken, namelijk
- het ontstaan van lineaire kanalisaties
- het ontstaan van feedback cycli
- het ontstaan van hypercycli.
Het ontstaan van deze verschillende niveau’s, bevestigt het theorema van Morowitz.

Het ontstaan van cycli werkt soms zelfversnellend (autokatalytisch),

Morowitz is verder gegaan in zijn redeneringen, en suggereert een thermodynamisch principe van maximum orde : een dissipatief systeem evolueert via quasi-stabiele toestanden die een maximale energie opslaan. Deze opslag van energie wordt omgezet in materiële structuur. Hij bouwt hiermee verder op de ideëen van Lotka (1925), die een energetische wet heeft voorgesteld voor alle levende systemen. Deze "maximum energiewet" stelt dat soorten levende systemen die willen overleven, een grote energetische output moeten hebben in de vorm van afmeting, groei, reproductie en zelfbehoud. In principe komt dit overeen met het principe van maximum orde dat Morowitz voorstelt.

Kay (1984) heeft hierop verder gebouwd door te stellen dat organismen hun "exergie maximaliseren" gedurende de ontwikkeling. Prigogine stelde parallel hiermee zijn "minimum entropie principe" voor, dat stelt dat bij mature systemen, de entropieproductie per eenheid wordt geminimaliseerd.

Ik heb deze verschillende wetmatigheden hier opgesomd, om aan te tonen dat dit een wetenschappelijk domein is dat nog in ontwikkeling is, en dat zowel de denkpatronen als het ermee gepaard gaande begrippenkader nog steeds in evolutie zijn.

De synthese die mijzelf het meest heeft kunnen overtuigen, is deze gemaakt door Eric Schneider en James Kay (1994).

Zij maken een onderscheid tussen the totale systeem, en de subsystemen die het systeem vormen :

Zij stellen dat het totale (levende) systeem gedurende zijn evolutie steeds meer entropie zal produceren, met andere woorden dat er een evolutie bestaat in de richting van een toename van exergie in het systeem (cfr. het "maximum exergie-principe").

Anderzijds zullen de subsystemen evolueren in de richting van een steeds lagere entropieproductie (cfr. het "minimum entropieproductie-principe") : de "specifieke entropieproductie" daalt.

Bovendien herformuleren ze de tweede wet van de thermodynamica als volgt :

"- Als een systeem verwijderd wordt van een evenwichtstoestand, zal het via alle mogelijke wegen trachten de opgelegde gradïenten te beperken.
- Als deze gradiënten toenemen, zal ook de capabiliteit van het systeem toenemen om zich te verzetten tegen de verwijdering van het evenwicht".

Als ik verder verwijs naar "de uitgebreide wetten van de thermodynamica", dan verwijs ik naar de 3 bovenstaande principes.

Ik heb bovenstaande principes geherformuleerd als het "principe van de fluxmaximalisatie".

Het belangrijkste onderscheid met Kay en Schneider is dat zij de stromen van informatie verwaarlozen en het principe louter toepassen op stromen van energie en materie.

Ilya Prigogine heeft wel vermeld dat, wanneer een systeem een transitie ondergaat naar een toestand van een andere coherentie, dit vooraf lijkt te gaan door een sterk toenemende -lange afstands communicatie - tussen de verschillende subsystemen waaruit het systeem bestaat.

Nu we de historische evolutie van het denken rond deze thermodynamicaprincipes hebben overlopen, kunnen stilaan wat dieper gaan graven in deze principes.

Ik zal dit voornamelijk doen met het schoolvoorbeeld bij uitstek, namelijk de vorming van "Bénard-cellen". Ik wil echter eerst het principe van de "koppeling" van energiestromen eens verduidelijken.

Terug naar de index van dit hoofdstuk

2. KOPPELING VAN STROMEN EN "WAAROM KAN EEN APPEL OMHOOG BEWEGEN?"

In het vorige hoofstuk hebben we beschreven hoe de Alfa-attractoren verantwoordelijk zijn voor de coherente evalutiepatronen van bepaalde systemen, waarbij uiteindelijk een toestand van (quasi)-evenwicht wordt bereikt.
Het typevoorbeeld was hierbij de appel die naar beneden viel.

Het is duidelijk geworden dat - omwille van de kenmerken van de attractoren die de appel beïnvloeden, de appel nooit spontaan "in de lucht naar omhoog zal bewegen".

Nochtans kan een appel ook opwaarts bewegen, door het principe van de koppeling van energiestromen.

Deze koppeling zal -net als het voorkomen van informatie - ervoor zorgen dat bepaalde evolutiepatronen tegen de spontane evolutierichting in kunnen doorgaan. Koppeling laat dus als het ware toe de spontane evolutierichting om te keren.

Om het principe van de "koppeling" te verduidelijken, maken we opnieuw gebruik van een éénvoudig voorbeeld : een appel die we omhoog laten bewegen.

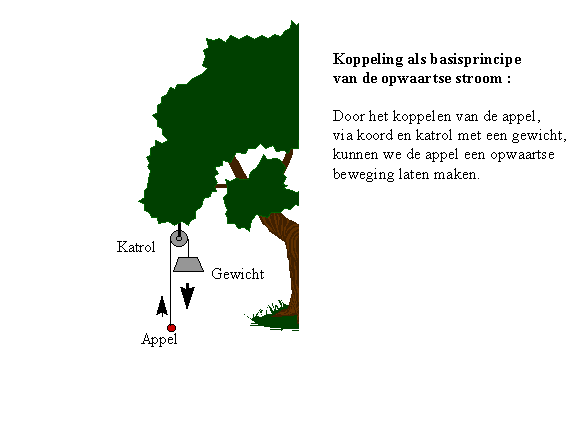
We binden de gevallen appel met een touwtje aan zijn steeltje, en verbinden hem via een katrol aan een zwaarder gewicht (cfr. onderstaande grafiek). Zo kunnen we de appel optillen. Het is een heel triviaal voorbeeld, voor een zeer belangrijk principe. Later zullen we voorbeelden zien waar de wijze van koppeling veel minder duidelijk is, vandaar dat we met een heel eenvoudig voorbeeld beginnen.

Figuur H6F3 : Koppeling van een opwaartse en een neerwaartse energieflux, kan de appel omhoog laten bewegen. Dit éénvoudig principe is van wezenlijk belang voor de opbouw van complexiteit in de natuur

Hierbij slagen we erin de appel een "niet-spontane" beweging te laten maken.

Het gehele systeem echter ( gewicht+appel+katrol+koord) vertoont gemiddeld gezien echter nog vooral kenmerken de tendens naar verspreiding. Uiteindelijk zal immers een toestand van (quasi)-evenwicht worden bereikt, doordat de energie en informatie aanwezig in het gewicht, langzaam verspreid worden, waardoor de beweging van het geheel zal worden gedempt.

In dit voorbeeld is het evolutiepatroon gedomineerd door de gravitatiekracht, met andere woorden door een zeer coherente Alfa-attractor. In de volgende paragrafen zullen stromen M/E/I worden beschreven, die het gevolg zijn van Beta-informatie.

De koppeling zal hierbij veel minder duidelijk zijn, doch in essentie blijft het basisprincipe geldig : een niet-spontane stroom kan enkel bestaan ten koste van, en door koppeling met, een nog grotere stroom die de totale verspreiding doet toenemen. We kunnen door voldoende toevoer of "voeding" van een coherente stroom van M/E/I, lokaal evolutiepatronen doen ontstaan met een hogere coherentie, zolang het bilan voor "systeem + omgeving" in de richting gaat van een toenemende verspreiding.

Deze "lokale tegenstroom in de evolutie" is de oorzaak van vele structuren die we rondom ons waarnemen, en is ook de bron van alle leven.

We zullen verder zien dat deze "opwaartse stroom" verantwoordelijk is voor heel wat fenomenen die ons dagdagelijks leven sterk beïnvloeden. Van auto’s, planten en dieren, draaikolken en en wolken, tot onze eigen gedachten en geschriften maken deel uit van de opwaartse stroom. Belangrijk genoeg dus om hier dieper op in te gaan.

Als we de spontane "neerwaartse stroom" vergelijken met een reusachtig mechanisch horloge dat langzaam afwindt, kunnen we de "opwaartse stroom" vergelijken met een reeks kleinere mechanische horloges, die precies door het afwinden van de grote horloge, regelmatig worden opgewonden.

Terug naar de index van dit hoofdstuk

3. KANALISATIE VAN DE EVOLUTIESTROOM

In deze paragraaf zullen we een aantal voorbeelden geven, waarbij door de koppeling met een "voedende stroom" van M/E/I, op een spontane wijze evolutiepatronen ontstaan met een hogere coherentie.

We zullen hierbij 2 schoolvoorbeelden geven van de vorming van spontane structuren in water. We zullen zien dat ook water, als vrij éénvoudige vloeistof, tot complexe patronen kan leiden.

Terug naar de index van dit hoofdstuk

3.1. Bénard cellen : de spontane vorming van "watersnelwegen"

De "Bénard-cellen" worden gevormd in een experiment waar we een laag water in een schaal van onderaan verwarmen. De verwarming is onze "voedende energiestroom" die de basis zal vormen voor de vorming van de cellen.

Wanneer we de verwarming onderaan de schaal aanzetten, zal de warmte aanvankelijk verspreid worden door "conductie", dit is door interactie tussen de molecules onderling, op relatief korte afstanden.
Bij toenemende verwarming, zal het temperatuurverschil tussen de onderste en de bovenste laag toenemen. De lokale interactie tussen de molecules is immers niet efficiënt genoeg om alle warmte te verspreiden of te "dissiperen".
Wanneer het temperatuurverschil (of de temperatuurgradiënt) een bepaalde kritische waarde bereikt, gebeurt iets merkwaardig.
In het water vormen zich als het ware kanalen, waarin het water stroomt. Van bovenaan gezien, zijn deze kanalen zichtbaar als zeshoekige cellen : de "Bénard-cellen". Door de vorming van deze "snelwegen van de verspreiding", kan de warmte die onderaan wordt toegevoerd, veel sneller naar boven worden gebracht, om daar verspreid te worden in de koude lucht. Deze waterstroom wordt een "convectiestroom" genoemd.

Door deze convectiestromen wordt het temperatuurverschil tussen de bovenste laag en de onderste laag verminderd, en krijgt de watermassa een homogenere temperatuur.

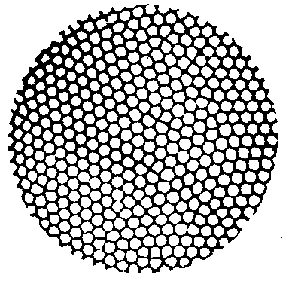
Figuur H6F4 : Een bovenaanzicht van Bénard cellen

De "stress" (in dit geval de temperatuurgradiënt) die we opgelegd hebben aan de watermassa, heeft dus geleid tot een macroscopisch zichtbaar dempingspatroon, waarbij een ontelbaar aantal watermolecules een coherente beweging maken : de flux van het water is hierbij maximaal, in functie van de energietoevoer aan de bodemplaat (cfr. het principe van de fluxmaximalisatie). Schneider en Kay hebben allerlei thermodynamische berekeningen uitgevoerd op het fenomeen van de Bénard-cellen, en hebben kunnen aantonen dat de vorming van Bénard-cellen inderdaad een grotere energiedissipatie tot gevolg geeft, dan wanneer de verspreiding enkel door conductie gebeurt. Hun conclusie luidt dan ook "hoe groter de temperatuurgradiënt wordt, hoe moeilijker het wordt om de gradiënt te verhogen". Niet alleen de toegevoerde energie wordt gedissipeerd, doch ook de opgelegde gradiënten. Schneider en Kay noemen dergelijke dissipatieve structuren daarom ook "gradiënt-dissipatoren".

Naarmate we de temperatuur verder laten toenemen, zijn er een aantal bijkomende transities, waarbij de hexagonale structuren leiden tot nieuwe "emergente" structuren die nog effectiever de toegevoerde warmte verspreiden. Uiteindelijk wordt het systeem volledig chaotisch, waarbij de energiedissipatie maximaal wordt.

Het besluit uit dit éénvoudige voorbeeld is dat nieuwe structuren of evolutiepatronen ontstaan, als gevolg van een demping van de opgelegde stress. De Bénard cel is dus een zeer goed voorbeeld van de uitgebreide wet van de thermodynamica, voor systemen die ver uit evenwicht zijn. Hoe verder het systeem van de evenwichtssituatie is verwijderd, hoe gesofisticeerder de mechanismen worden om de opgelegde stress te beperken, met andere woorden, hoe gesofisticeerder de dempingspatronen.

Opnieuw kunnen we ons afvragen waar de "choreograaf" zit die deze indrukwekkende stroom van een massaal aantal molecules dirigeert. Het antwoord kan echter niet hetzelfde zijn als bij bijvoorbeeld de vorming van een ijskristal. Alfa-informatie ligt dus niet aan de basis van deze dissipatie-patronen.

Wat dan wel ?

Prigogine vergelijkt de deeltjes die zich dicht bij een evenwichtsstoestand bevinden, zoals de watermolecules in een stille watermassa, met "slaapwandelaars" of "hypnonen". De deeltjes trekken zich immers niets van elkaar aan. Wanneer we echter energie toevoeren aan het systeem, waardoor het systeem zich verder van de evenwichtsstoestand verwijdert, krijgen de deeltjes wel betekenis voor elkaar. Hun gedrag beïnvloedt elkaar, "ze gaan communiceren over langere afstanden", wat leidt tot een nieuwe ordening van grote groepen deeltjes, met een macroscopisch zichtbare ordening tot gevolg.

In het geval van de Bénard cellen is het patroon dat we waarnemen volledig bepaald door de hoeveelheid warmte-energie die we toevoeren. Naarmate de temperatuurgradiënt die we opbouwen, ontstaan conductie- of convectiepatronen.

Het is dus het stromingsproces zelf dat verantwoordelijk is voor de aard van de interactiepatronen !
De informatie die de patronen bepaalt, komt tot stand als gevolg van een dynamisch proces. Het patroon dat we zien is geen weerspiegeling van de vorm van de molecules maar van de interacties tussen de molecules. Deze "procesinformatie" zal hier voortaan Beta-informatie worden genoemd.

Deze Beta-informatie kan enkel bestaan, zolang de voedende energiestroom bestaat.

Spontane kanalisatie van water, zoals zich dit voordoet bij de vorming van Bénard cellen, vinden we ook in de praktijk terug. Ook andere processen kunnen echter tot kanalen leiden.

In sommige bodems van uitgedroogde meren vinden we zogenaamde "steenkussens" terug. Deze min of meer zeshoekige concentraties van stenen zijn het gevolg van convectiestromen. Gedurende een langzame evolutie zijn de stenen door de Bénard-achtige convectiestromen in het oorspronkelijke meer bij elkaar geconcentreerd. De steenkussens zijn op die manier een getuigenis van het Bénard-proces.

De vorming van rivieren in een landschap is ook een duidelijke vorm van kanalisatie, die echter geen temperatuurgradïent aan de basis heeft zoals de Bénard-cellen. Aan de basis van de vorming van rivieren, liggen hoogteverschillen (een "hoogtegradiënt").
In een jong landschap zullen stromen en rivieren ontstaan ten gevolge van een fluxmaximalisatieproces. Aanvankelijk zal een eng, meestal V-vormig kanaal worden gevormd, dat bovendien vrij diep is. In een meer matuur landschap zal deze rivier een boomachtig patroon van zijrivieren vormen.
In een oud landschap, zal de rivier meestal breed zijn en talrijke meanders hebben.
Gedurende zijn evolutie heeft de rivier het landschap sterk ge-erodeerd, en is de "weerstand tegen vervorming" van het landschap sterk op de proef gesteld.
De ultieme vorm van erosie zou zijn dat het hoogteverschil volledig zou zijn weggewerkt : in dit geval zou de gradiënt volledig verdwenen zijn : de waterstroom als ultieme "gradiëntdissipator". In reële landschappen zal men dit, omwille van de vele gesteenten in de bodem, niet aantreffen.

Ook de vorming van gletsjers zijn mooie voorbeelden van macroscopische kanalisatiepatronen in de natuur.

Terug naar de index van dit hoofdstuk

3.2. Het Taylor-couette systeem : complexere patronen in water

In 1920 was er een onderzoeker aan de Cambridge University, namlijk Geoffrey Ingram Taylor, die dit proces meer in detail wilde bestuderen. Hij gebruikte hiervoor een systeem - het "Taylor-Couette" systeem genoemd, dat toelaat de vorming van dergelijke emergente waterpatronen beter te bestuderen. Het idee van de studie van water tussen twee cilinders is reeds vermeld in Newtons’ "Principia", doch werd voor het eerst in de praktijk gebracht door de Fransman Maurice Couette op het einde van de 19de eeuw.

Het systeem bestaat uit 2 concentrische cylinders, waartussen een laag vloeistof beweegt. Naarmate de draaisnelheid van de cilinders varieert, en de cilinders al dan niet in gelijke richting draaien, ontstaat een verassende verscheidendheid aan stromingspatronen.

Beide cilinders kunnen onafhankelijk van elkaar versneld of vertraagd worden, wat tot een zeer groot aantal waterpatronen leidt.

Wanneer de cilinders stil blijven staan tegenover elkaar, is het water in evenwicht.

Naarmate we energie toevoeren door de snelheid van de binnenste cilinder op te drijven, zal het water langzaam beginnen bewegen, zonder dat er een patroon zichtbaar is voor de waarnemer. Dit wordt de "Couette-stroming" genoemd. Verhogen we de snelheid van de buitenste cilinder, dan krijgen we op een bepaald ogenblik een verandering van stromingspatroon : er verschijnen horizontale strepen in de watercilinder, de zogenaamde Taylorwerverlingen. Deze strepen herhalen zich op vaste afstanden, en vormen een regelmatig patroon.

Verhogen we de snelheid nog verder, dan verandert op een bepaald moment het patroon opnieuw, en krijgen we "golvende wervelingen" te zien. We zien op elke plaats een golvend patroon verschijnen, dat duidelijk nog meer dynamiek vertoont dan de Taylor-stroming.

Zo gaat het verder : naarmate we meer energie toevoeren, wordt het stromingspatroon complexer en dynamischer.

Figuur H6F5 : Enkele stromingen in het Taylor-Couette systeem. Van links naar rechts : de "Couette-stoming" , de "Taylor-stroming", de "golvende werveling" en een "spiraalstroming".

Naast het verhogen van de snelheid van de binnenste cilinder, kunnen we ook de snelheid van de buitenste cilinder gaan varieren, wat het scala aan patronen nog opdrijft.

Wanneer we energie toevoeren van buitenaf, ontstaat vanaf een kritisch punt nieuwe Beta-informatie, en krijgen we als waarnemer een nieuw patroon te zien. De Beta-informatie vormt een nieuwe Beta-attractor, die het nieuwe patroon doet verschijnen.

Dit gaat opnieuw gepaard met een symmetriebreking. De originele grote symmetrie van de Couettestroming, wordt bij overgang naar de Taylorstroming verbroken tot een patroon met een lagere symmetrie. Deze Taylorstroming is voor de mens boeiender patroon, doch onze definitie van symmetrie volgend, moeten we besluiten dat de symmetrie wordt gebroken (en dus verlaagd wordt).

Naarmate we meer energie toevoeren in het systeem, en dus verder weg gaan van de roerloze situatie van het stille water, komen we meer dergelijke bifurcaties tegen. Bij elke bifurcatie ontstaat dus een nieuwe stabiele Beta-attractor, als gevolg van nieuwe "procesinformatie".

Op deze wijze krijgen we uiteindelijk een "boom van evolutiewegen" of "bifurcatieboom", naarmate we ons verder van de evenwichtssituatie bevinden. Elke splitsing is dus gekenmerkt door het onstaan van een nieuw paar Beta-attractoren, waarbij enkel de meest stabiele attractor tot de realisatie van een evolutiepatroon zal leiden : enkel de stabiele (dominante) attractoren worden geselecteerd.

De bifurcatieboom is dus de grafische weergave van het feit dat de evolutie "een zich vertakkend netwerk van evolutiewegen" is.

Het is voornamelijk Ilya Prigogine geweest die de inzichten rond het gedrag van systemen "ver uit evenwicht" heeft beschreven.
Elke transitie is gekenmerkt door een bifurcatiepunt, waarbij nieuwe Beta-informatie en een nieuwe attractor wordt gevormd.

Heel kenmerkend voor het bifurcatiediagram, is dat bij deze transitie, steeds 2 evolutiepatronen mogelijk zijn, namelijk één evolutiepatroon en zijn symmetrische spiegelbeeld. Elke symmetriebreking heeft zijn symmetrische tegenpool. Het woord "bifurcatie" betekent dan ook "in twee splitsen". Welke weg gekozen zal worden is dikwijls afhankelijk van de initiële condities : deze bepalen welke weg er stabiel is.

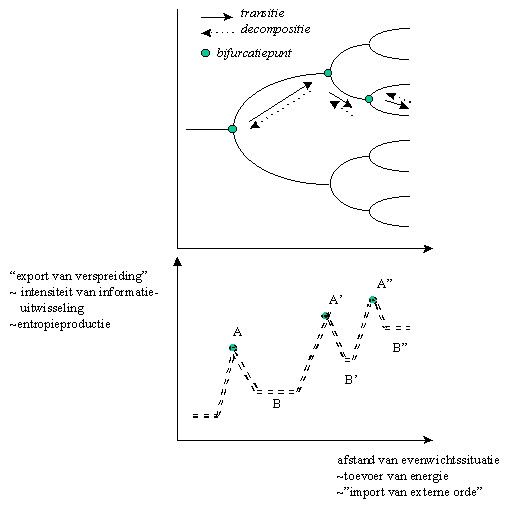
Als we de toevoer van energie verminderen, kan het systeem terug naar zijn oorspronkelijke toestand terugkeren : dit hebben we reeds eerder "decompostie" genoemd. Dit wordt grafisch voorgesteld in onderstaande figuur.

Figuur H6F6 : Een voorbeeld van een bifurcatieboom (bovenaan) en het verloop van de entropieproductie in de diverse evolutiestadia (onderaan)

Deze decompositie gaat natuurlijk niet altijd exact volgens deze opeenvolgende sequenties door. Als de energietoevoer plots wordt gestopt, zullen de intermediare transitiepatronen geen tijd hebben om zich te vormen.

Het is dus net alsof het systeem een primitief geheugen heeft. Het is echter de reeds genoemde "Beta-attractor" die steeds onder dezelfde condities terug verschijnt, en daardoor, bij vermindering van de energietoevoer, overgaat in een andere Beta-attractor die verantwoordelijk is voor het vorige patroon.
Nochtans is deze decompositie geen onbelangrijk fenomeen. Het impliceert dat de evolutie kan terugvallen op zijn eigen historiek. Door deze "zelfreferentie" komen de evolutiepatronen in coherente sequenties voor.

Prigogine heeft aangetoond dat vele complexe patronen rondom ons, het gevolg zijn van processen die ver uit evenwicht zijn. Dit blijkt duidelijk uit bijvoorbeeld het Taylor-Couette systeem, waar een eenvoudige vloeistof als water, tot een grote rijkdom aan patronen kan leiden, indien ze ver van de evenwichtssituatie wordt gebracht. Bovendien bevinden alle levende wezens zich "ver uit evenwicht" : hun dagelijks leven bestaat dan ook voornamelijk uit het behouden van deze niet-evenwichtssituatie ; voedsel zoeken is immers voor bijvoorbeeld de meeste dieren de voornaamste dagtaak.

Het ontstaan van de coherente patronen in het Taylor-Couette systeem kunnen we toewijzen aan het principe van de flux-maximalisatie. Door het collectief egoïsme waarmee alle watermolecules de opgelegde stress trachten te minimaliseren, ontstaat een coherent evolutiepatroon.

Prigogine heeft aangetoond dat het ontstaan van deze evolutiepatronen, in een aantal fasen verloopt,die zich onderscheiden qua "export van de verspreiding" of in klassieke thermodynamische termen, de "entropie-productie".

Bij stil water, bewegen de molecules in het water kris-kras door elkaar. Er is een maximale verspreiding van de molecules in het water, en er is geen "export van verspreiding", noch "import van orde" in het systeem. Dit is de typisch niet-geïnformeerde beweging, waarvoor Boltzmann belangrijke basisprincipes heeft vastgelegd.

Dit is de periode van maximale entropie of verspreiding binnen in het systeem.

Bij toevoer van energie, zullen vanaf een kritisch punt (het bifurcatiepunt), de watermolecules met elkaar gaan "communiceren" : de "slaapwandelaars" worden wakker en wisselen Beta-informatie uit. Een transitie heeft plaats.

Tijdens deze transitie is de entropieproductie, of export naar van verspreiding, naar de omgeving het grootst (zie pieken A, A’ en A") in de grafiek.
Dit is de periode van "maximale entropieproductie" of maximale export van verspreiding.

Na de transitie komt er een periode van relatief dynamisch evenwicht. De nieuwe patronen in het systeem, zorgen voor een nieuwe manier om entropie of verspreiding te exporteren.
Dit is de periode van de "minimale entropieproductie" of minimale export van verspreiding.
De Taylorstroming bijvoorbeeld, waarbij alle molecules als het ware in parallelle snelwegen zijn geordend, is hiervoor efficiënter dan de Couette stroming ; op zijn beurt is de golvende beweging efficiënter voor de "export" van grotere hoeveelheden verspreiding, dan de Taylorstroming.

Kay en Schneider hebben hierbij - vanuit hun ecologische achtergrond - toegevoegd dat de fase van "minimale entropieproductie" in natuurlijke systemen (wat het Taylor-Couette systeem niet is), gepaard gaat met een groei van het systeem. Deze groei van het systeem gaat gepaard met een stijgende maturiteit van de evolutiepatronen. Bij toenemende maturiteit wordt de specifieke entropieproductie van de subsystemen wordt hierbij inderdaad steeds kleiner (cfr. het prinicipe van de minimale entropieproductie), doch doordat het systeem in zijn geheel groeit, neemt de totale entropieproductie van het totale systeem toe.

Ook in complexere systemen vinden we deze evolutiestadia terug : daarom nog 2 extra voorbeelden.

Onderzoek bij bevruchte kippe-eieren heeft bijvoorbeeld uitgewezen dat 4 dagen na de bevruchting, de warmteproductie 4 keer groter is dan 16 dagen na de bevruchting. De warmte-afgifte naar de omgeving toe is hierbij een maat voor de verspreiding van export (entropieproductie). Deze is dus de eerste 4 dagen veel hoger dan in het daarop volgende evolutiestadium (dat nog verre van matuur is).

Ook in een bedrijfsleven is het bekend dat grote organisatorische wijzigingen initieel steeds gepaard moeten gaan met een grote energietoevoer, en zeer duidelijke communicatie (grote informatie-uitwisseling) over het waarom. Elke vorm van "veranderingsmanagement" wekt steeds wrijvingen op bij de betrokken personeelsleden. Niet alleen dus de energietoevoer om de verandering te initiëren, doch ook deze weerstanden veroorzaken "verspreiding" van de originele boodschap en doelstellingen van de geplande verandering. Deze verspreiding in het bedrijf komt ook tot uiting doordat de bijvoorbeeld de boodschap over de organisatiewijziging zich heel snel door het bedrijf zal verspreiden (soms sneller dan gepland), en door het feit dat er bij deze ruimtelijke verspreiding, variaties zullen ontstaan op de inhoud van de boodschap die door het management van de organisatie is gecommuniceerd. Wellicht is het woord "slaapwandelaar" niet van toepassing voor de gemiddelde werknemer, doch communicaties met betrekking tot een reorganisatie kunnen een schokgolf van alertheid veroorzaken.
Na een eerste fase van turbulentie die volgt net na het doorvoeren van de verandering, treedt ook in het bedrijfsleven een fase van quasi-stabiliteit op.

Terug naar de index van dit hoofdstuk

3.3. Kwantumsprongen in de evolutie

Bij elk bifurcatiepunt kunnen 2 evolutiewegen worden ingeslagen. Hierbij vertonen de 2 mogelijke alternatieven gelijkaardige symmetrieën.

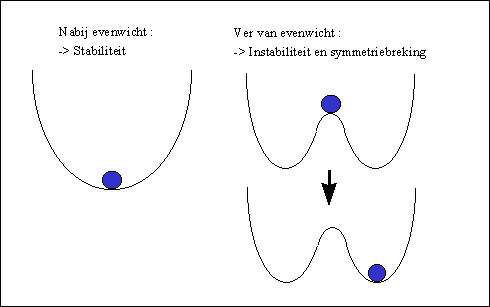
Bij het bifurcatiepunt bevindt het systeem zich in een instabiele toestand, te vergelijken met de situatie van de bal in onderstaande figuur rechts.

Figuur H6F7 : Stabiliteit en symmetrie (links) ; instabiliteit en assymetrie (rechts)

Wanneer de bal zich in een dal bevind, is de situatie stabiel. Een kleine duw tegen de bal naar de linker of rechterkant, verstoort de stabiliteit van de bal niet : hij rolt terug naar zijn evenwichtspositie.

In de situatie ver van evenwicht echter, bevindt de bal zich in een instabiele positie. Een kleine verstoring van het evenwicht, zal hier een groot gevolg hebben voor de positie van de bal : hij zal naar de linker of de rechterkant bewegen. Hierbij wordt de oorspronkelijke spiegelsymmetrie verbroken, doch komt de bal opnieuw in een stabiele positie terecht.

Symmetrie wordt dus geruild voor stabiliteit bij een bifurcatiepunt.

De natuurkundige Pierre Curie (vooral bekend door zijn vrouw Marie Curie) deed in 1894 twee beweringen in verband met de verbreking van de symmetrie die kenmerkend is voor dergelijke bifurcatiepunten. Deze principes zijn intussen bekend als "de principes van Curie". Deze principes wijzen erop dat bij de verbreking van de symmetrie bij een bifurcatiepunt, de symmetrie van de nieuwe quasistabiele toestand :
- lager zal zijn dan van de vorige toestand
- een symmetrie zal hebben die tot dezelfde symmetriegroep behoort.
De uiteindelijke symmetrie zal dus lager zijn dan de oorspronkelijke, doch zal wel verwant zijn met de oorspronkelijke.

Terug nu naar het Taylor-Couette systeem.

Wetenschappers hebben mathematische modellen ontwikkeld, die het Taylor-Couette systeem zo goed mogelijk moet kunnen simuleren.

Men is er in geslaagd de bijhorende waterpatronen grafisch weer te geven. Hieruit blijkt bijvoorbeeld bij de overgang van de Couettestroming naar een nieuw regime, 2 stromingspatronen mogelijk zijn. De ene is de Taylorstroming, die gekenmerkt is door horizontale strepen water. De andere is een gelijkaardig patroon, doch waarbij de strepen schuin omhoog lopen, en dus een spiraal vormen. Beide patronen vertonen een symmetrie die lager is dan die van de oorspronkelijke Couette stroming. Bij een volgend bifurcatiepunt wordt zal de symmetrie opnieuw vervallen naar een lager niveau.

Deze stapsgewijze evolutie is zo kenmerkend, dat we de transities terecht "kwantumsprongen" in de evolutie kunnen noemen.

Op zich is dit wel merkwaardig. Op het meest fundamentele vlak in de natuurkunde (namelijk de deeltjesfysica) , heeft men in het begin van deze eeuw ontdekt dat de energie van deeltjes in sprongen of kwanta toeneemt. Vandaar dat men spreekt van bijvoorbeeld quantummechanica.

Bovendien geldt bij elementaire deeltjes het onzekerheidsprincipe van Heisenberg : het is onmogelijk om tegelijkertijd plaats en tijdstip van de evolutiebaan van een elementair deeltje te kennen : het is dus onmogelijk om perfect het traject te voorspellen dat door een deeltje gevolgd zal worden.

Wat we nu merken is dat in alle stadia van de evolutie, er sprake kan zijn van kwantumsprongen : tal van evoluties verlopen sprongsgewijs.

Bovendien is er niet enkel op het niveau van elementaire deeltjes een fundamentele onzekerheid - en dus onvoorspelbaarheid - van de evolutie. Bij elk bifurcatiepunt zijn er verschillende mogelijkheden, en is het voor de waarnemer niet te voorspellen welk evolutietraject er zal worden gevolgd.

Onzekerheid en kwantumsprongen vinden we dus op verschillende niveau’s in de evolutie terug, en zijn daarom te beschouwen als essentiële kenmerken van de gemiddelde evolutie.

Terug naar de index van dit hoofdstuk

Ga naar het vervolg op de volgende pagina