4. TERUGKOPPELING EN VORMING VAN CYCLI
De opwaartse stroom wordt complexer

 

In de vorige paragraaf maakten we kennis met de vorming van kanalen in Bénard-convectiestromen. In werkelijkheid zijn deze kanalen een onderdeel van een cyclische stroming binnen het water dat deel uitmaakt van de proefopstelling. Het water dat naar boven stroomt via bepaalde kanalen, stroomt via andere kanalen terug naar beneden.

Hetzelfde kan gezegd worden van de vorming van rivieren als voorbeeld van de spontane vorming van kanalen. Ook het water dat in deze rivieren stroomt, maakt deel uit van een wereldwijde "watercyclus", waarbij water door verdamping uit de zee, via neerslag uit de wolken op het land terecht komt. Hier start de stroom via kanalen of rivieren, tot deze opnieuw uitmonden in de zee.

Het voorkomen van cycli beïnvloedt ons dagelijks leven zeer uitgebreid.

Morowitz heeft reeds in 1968 aangetoond dat als een stroom van energie door een systeem leidt, dit uiteindelijk zal resulteren in een cyclische stroom : dit is bekend als het Theorema van Morowitz.

Het cyclisch gedrag van deze processen leidt niet enkel tot de ontwikkeling van een hiërarchie in de processen, doch draagt ook bij tot de complexiteit en stabiliteit. Bovendien worden vele van deze cycli zelfversnellend of autokatalytisch. Een verklaring voor dit autokatalytisch cyclisch gedrag is in veel gevallen het volgende : één van de reactieproducten van het proces, wordt ook de "voeding" van een andere stap in het proces. Als gevolg hiervan wordt de voeding als het ware in het proces "gezogen", komt er een hogere toevoer van voeding in het proces en wordt het proces verneld.
De vorming van cycli is daarom een zeer belangrijke stap in de toename van complexiteit en de vorming van emergente eigenschappen in Beta-processen.

We zullen in de volgende paragrafen ook stap voor stap met verschillende aspecten van deze toenemende complexiteit kennis maken.

Terug naar de index van dit hoofdstuk

 

4.1. Videoterugkoppeling : van eenvoud naar complexiteit

 

Wat gebeurt er wanneer we een videocamera net voor een televisiescherm plaatsen, zodat de camera zijn eigen beeld aan het filmen is ?

Intuïtief zouden de meesten mensen antwoorden dat er niks gebeurt, of dat een beeld van het televisiescherm op het scherm verschijnt.

De werkelijkheid is anders. Naarmate we de scherpte en afstand van het scherm wijzigingen, verschijnen bij bepaalde instellingen heel complexe beelden, die weinig of geen verband houden met het televisiescherm dat we aan het filmen zijn. Er kunnen diverse types stabiele of dynamische patronen op het scherm verschijnen.

Wat er in werkelijkheid gaande is, is te vergelijken met het Taylor-Couette systeem. Bij bepaalde instellingen van de camera, botsen we op een nieuwe Beta-attractor, die een nieuw stabiel patroon doet onstaan. De complexiteit van de patronen in deze ogenschijnlijk zeer eenvoudige situatie wordt vrij complex, precies door het element terugkoppeling (feedback).

De terugkoppeling beïnvloedt niet enkel de complexiteit van de patronen, doch ook de stabiliteit.

Terugkoppeling verhoogt in bepaalde toestanden de stabiliteit van de stroom van materie, energie en informatie : dit is de reden waarom er stabiele attractoren ontstaan.

Het stabiliserende of regelende element van terugkoppeling wordt zowel door de natuur als door de mens veelvuldig gebruikt om de impact van storingen vanuit de omgeving op het systeem te beperken, zodat de "opwaartse stroom" kunstmatig op een bepaald niveau wordt gehouden.

• Indien er bijvoorbeeld een tekort is aan materie/energie bij planten of dieren, zullen ze ervoor zorgen dat dit tekort wordt verminderd : planten groeien daarom naar het licht, tijgers zoeken een nieuwe prooi, een land bouwt een nieuwe haven om meer grondstoffen in te voeren.
• Wanneer er bijvoorbeeld een overmaat is aan materie/energie, zullen de planten of dieren acties nemen om de instroom van materie en energie te beperken. Een amoebe zal zich uit een zuur milieu verwijderen, de mens opent een paraplu of gaat schuilen wanneer het regent.

De complicerende en stabiliserende invloed van de terugkoppeling op de evolutiestroom is voorgesteld in onderstaande veralgemenende figuur. Natuurlijk is het zo dat terugkoppeling niet in alle situaties zowel de complexiteit, als het aantal attractoren doet toenemen, en daarbij ook de situatie stabiliseert. Wel is het zo dat het invloed kan hebben op de verschillende kenmerken, en dat het dus een belangrijke invloed heeft op de stroom van materie, energie en informatie.

Figuur H6F8 : terugkoppeling in de evolutiestroom

Het is duidelijk dat het toenemend aantal terugkoppelingen in de evolutiestroom tot een zelfversnellend of autokatalisch proces leidt : het is een vicieuze cirkel die steeds sneller draait en bovendien leidt tot additionele emergente niveau’s in de evolutie.

In de volgende paragrafen zullen nog een aantal voorbeelden worden gegeven, die de invloed van terugkoppeling op complexiteit of stabilisatie van processen kunnen verduidelijken.

In bepaalde processen in de natuur is er niet enkel sprake van terug-koppeling (feedback) maar ook van voorwaartse koppeling (feedforward).

Terug naar de index van dit hoofdstuk

 

4.2. Fractalen en zelfreferentie van de vorm

Het belangrijkste kenmerk van terugkoppeling is zelfreferentie : het systeem of de stroom valt terug op zichzelf. Deze zelfreferentie is een belangrijk kenmerk voor dynamische processen in de natuur, doch ook voor statische vormen. In de meetkunde die we tijdens onze jeugdjaren op school hebben gekregen, was er voornamelijk aandacht voor regelmatige vormen (cirkels, vierkanten, kubussen) en als het over afstanden ging, werd er meestal een vogelvlucht berekend.

Nochtans is de natuur grilliger dan deze ge-idealiseerde mathematische vormen. De vorm van een kustlijn is niet recht doch verloopt kronkelend ; bloemkolen, bomen, varens, wolken en bergen vertonen ingewikkelde vertakkingen. In al zijn grilligheid hebben deze complexe vormen nochtans één kenmerk gemeen : zelfreferentie van de vorm. Dit wordt algemeen aangeduid door te zeggen dat ze een fractaalvorm vertonen, of zelfgelijkvormig zijn.

Dit betekent dat deze vormen ogenschijnlijk heel complex zijn, doch dat een relatief éénvoudig bouwschema aan de basis ligt. Dit bouwplan wordt op verschillende schaalgroottes herhaald, met een complex patroon als gevolg. Zoals we reeds eerder gezien hebben, is deze herhaling een gevolg van de beperkte hoeveelheid informatie die in het systeem aanwezig is, waardoor dezelfde patronen worden herhaald. Het is een uiting van de "luiheid" van de natuur, met betrekking tot het zoeken naar nieuwe patronen.

Een bekend voorbeeld hiervan is de sneeuwvlok van Koch in onderstaande figuur.

Deze figuur wordt opgebouwd door telkens een driehoekje te plaatsen op de zijden van grotere driehoeken. Als je dit proces oneindig veel herhaalt, bekom je een mooie sneeuwvlok waarvan de omtrek oneindig lang is. De oorzaak is dat, hoe veel we de sneeuwvlok ook uitvergroten, we telkens opnieuw een kleiner driehoekje tegenkomen dat toch nog een bepaalde lengte heeft.

 

Figuur H6F9 : de sneeuwvlok van Koch

Dergelijke grafische vormen kan je dus niet kenmerken door hun lengte, doch wel door de mate van zelfgelijkvormigheid : hoeveel moet je de schaalgrootte verkleinen om opnieuw dezelfde vorm te verkrijgen. Aangezien de figuur stapsgewijs is opgebouwd, kunnen we bijvoorbeeld meten hoeveel de lengte van de kromme toeneemt met elke stap toeneemt. Als de lengte van de zijde "L" is, dan kan voor elke stap de lengte van de kromme verkregen worden door "L" met het aantal zijden te vermenigvuldigen : de totale lengte wordt dan L^1-D, waarbij D = 1,261...

Deze formule werd bedacht door Ralph Richardson, bij zijn onderzoek naar de lengte van kustlijnen.

De letter D is de afkorting voor "Dimensie". Fractaalvormen worden beschouwd als vormen met een gebroken dimensie (vandaar het woord fractaal). De Koch kromme heeft dus een dimensie die ligt tussen 1 en 2, en houdt dus ergens het midden tussen een lijn en een kromme (volgens deze redenering).

Dit als voorbeeld om aan te duiden hoe zelfreferentie de complexiteit kan doen toenemen, en dat zelfreferentie in de natuur veel voorkomt. Dat fractaalgeometrieën in de natuur veel voorkomen, wordt gedemonstreerd door onderstaande foto. Het beeld is volledig gegenereerd door een computer die gebruik maakt van fractaalgeometrieën.

Figuur H6F10 : een landschap met de computer getekend op basis van fractaalberekeningen

Terug naar de index van dit hoofdstuk

 

4.3. Haaien en garnalen

De fractalen waren een statisch voorbeeld van hoe terugkoppeling de complexiteit van een systeem kan verhogen. Laten we nu echter eens een dynamisch voorbeeld bekijken.

Stellen we ons een zee voor waarin haaien en garnalen voorkomen, en laten we het verloop van het aantal haaien en garnalen eens opvolgen. Het verloop is aangeduid in de onderstaande grafieken. (Het is duidelijk dat deze grafieken gelden voor om het even welke roofdier-prooi relatie, zoals vossen/konijnen, vogels/insecten).

Figuur H6F11 : De evolutie van een populatie predatoren en prooidieren is aan elkaar gekoppeld, wat leidt tot een periodiek evolutiepatroon, afhankelijk van de begincondities

Stel dat we starten van een situatie waarbij we een bepaald aantal haaien en garnalen (figuur a) hebben.

De haaien doen zich tegoed aan de garnalen, waardoor de haaienpopulatie stijgt in aantal, en de garnalenpopulatie daalt in aantal (figuur b). Op een zeker ogenblik zal er een tekort ontstaan in garnalen, waardoor veel haaien bij gebrek aan voedsel zullen sterven. Daardoor kunnen de garnalen weer enige tijd rustig leven en zich voortplanten, waardoor hun populatie opnieuw stijgt. We krijgen dus een cyclische evolutie : het aantal haaien gaat op en neer, en het aantal garnalen vertoont een tegenovergestelde evolutie. In de grafiek met in de ene as het aantal haaien, en de andere het aantal garnalen, verkrijgen we een cirkel, die de cyclische beweging weergeeft.

Wanneer we van een andere begintoestand vertrekken, met bijvoorbeeld een groter aantal haaien en garnalen, krijgen we opnieuw een cyclische evolutie : nu echter zal de cyclus wat groter zijn.

Afhankelijk dus van de begintoestand, krijgen we een verschillend evolutiepatroon. Qua vorm is het evolutiepatroon echter steeds hetzelfde, en wordt het evolutietraject "aangetrokken" rond de attractor.

Het punt in het centrum van de curves c is in dit type grafische weergave van de Beta-attractor die dit systeem kenmerkt. De terugkoppeling in dit voorbeeld leidt tot een complex periodiek patroon : de aanwezigheid van de attractor zorgt echter voor een zekere stabiliteit in het patroon.

De mathematische vergelijkingen voor deze evolutie zijn reeds rond 1920 opgesteld door Vito Volterra, een Italiaans mathematicus.

P + G -> 2G

G + H -> 2H

H -> D

Hierbij staat "P" voor het plankton dat de garnalen ("G") eten om zich te vermenigvuldigen. "H" staat voor de haaien die zich vermeningvuldigen als er voldoende garnalen zijn. Bij tekort aan garnalen, of door de ouderdom, wacht de haaien echter de dood ("D").

Het terugkoppelingsaspect zit in het feit dat bij elke generatie, het aantal haaien of garnalen, afhankelijk is van het aantal haaien of garnalen in de vorige generatie. Het aantal haaien en garnalen, en de hoeveelheid plankton, is dan ook de "beta-informatie" die de dynamiek van het systeem bepaalt : het is de informatie waarnaar het systeem refereert om zijn evolutiepatroon te bepalen : het is de spiegel van zijn zelfreferentie.

Merk op dat ook dit evolutiepatroon "gevoed" moet worden om te bestaan : de haaien moeten garnalen eten, en de garnalen moeten plankton eten : zoniet stopt deze verschijningsvorm van "de opwaartse stroom". De groei van de garnalen is dus gekoppeld aan de aanwezigheid van plankton, en de groei van de populatie haaien is gekoppeld aan deze van de populatie garnalen.

Terug naar de index van dit hoofdstuk

 

4.4. Vreemde attractoren

De grafische weergave van de Beta-attractor in het fasediagram is in het geval van de haaien en dit geval zeer éénvoudig : het is namelijk een punt (wat wijst op een cyclisch evolutiepatroon). De grafische weergave van veel Beta-attractoren is soms veel complexer. Hoe complexer echter de grafische weergave van de attractor, hoe complexer de regelmaat in het evolutiepatroon : de regelmaat en dus ook de symmetrie is dus verder en verder te zoeken. Bepaalde evoluties zijn zo complex, dat het evolutiepatroon zelf geen enkele regelmaat meer vertoont : soms vertoont enkel de grafische weergave van de attractor nog een regelmaat.

In dit geval spreekt van "vreemde attractoren" (bij de eerste waarneming ervan, vond men ze vreemd).

Een voorbeeld hiervan is de "Lorenz-attractor".
Edwin Lorenz heeft als meteoroloog gewerkt aan het Massachusetts Institute of Technology (MIT). Als meteoroloog stelde hij belang in het verschijnsel van de atmosferische convectie : de zon verwarmt de grond, waardoor de lagere luchtlagen van de atmosfeer warmer en lichter worden dan de hogere luchtlagen. Dit heeft een opwaartse beweging van de warmere en lichtere lucht tot gevolg, voornamelijk in de tropen (een gelijkaardige convectiestroom stelden we vast in de Bénard-cellen). Deze warme convectiestroom stroomt in de richting van de polen. Bij de poolregionen koelt deze lucht opnieuw af, en beweegt vanuit de atmosfeer naar beneden. Vanuit de polen stroomt deze koude lucht opnieuw naar de evenaar. Op deze manier wordt warmte-energie van de tropen naar de polen gevoerd, en wordt de temperatuursgradiënt tussen bovenlagen en onderlagen enerzijds, en tussen tropen en polen anderzijds, geminimalizeerd.

Door een aantal vereenvoudigingen door te voeren, kwam Lorenz tot de vergelijkingen van het convectiesysteem. Deze vergelijkingen vertonenen opnieuw zelfreferentie :

dx/dt = - (x-y)

dy/dt = -xz + rx -y

dz/dt = xy - bz

waarbij x(t), y(t) en z(t) functies zijn van de locale temperatuur en de snelheid aangeven : r is evenredig met het temperatuurverschil tussen bodem en het bovenvlak. Mathematisch gezien zijn dit vrij complexe vergelijkingen, die een hoge mate van zelfreferentie bevatten. Het zijn niet-lineaire vergelijkingen, die enkel door computersimulaties kunnen worden opgelost. Systemen die zich ver uit evenwicht bevinden zijn, als ze al mathematisch te beschrijven zijn, veelal dergelijke niet-lineaire vergelijkingen.

De grafische weergave van de attractor zien we in onderstaande figuur.

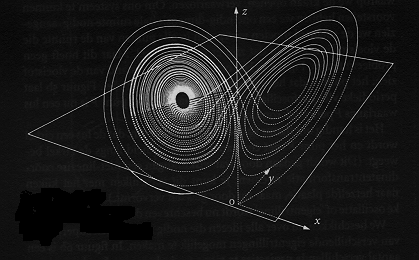
Figuur H6F12 : grafische weergave van de Lorenz-attractor

De Lorentz attractor heeft de vorm van een vlinder (het is een driedimensionele vorm). De evolutietrajecten (of trajectori) draaien rond de twee vleugels, die middenin samensmelten. Van welke richting je ook vertrekt, er moet middenin steeds besloten worden in welke richting er zal worden verdergegaan. Als je bovendien vanaf 2 punten vertrekt die dicht bij elkaar liggen, zullen deze zich na enige tijd ver van elkaar verwijderen : hun evolutietraject is meer en meer onafhankelijk. Het gevolg is de een evolutietraject voor één deeltje niet voorspelbaar is op langere termijn. Het evolutiepatroon is chaotisch. Dit is een kenmerk van alle vreemde attractoren. De attractor zelf vertoont nog een symmetrisch en regelmatige vorm, doch het eruit voortvloeiende evolutiepatroon is chaotisch.

Dergelijke patronen zijn voorbeelden van wat men "deterministische chaos" noemt. Het is mogelijk om een deterministisch model op te stellen en de attractoren van het systeem te vinden. De invloed van heel kleine factoren in het systeem blijkt echter soms zo belangrijk te zijn, dat het gedrag op lange termijn niet voorspelbaar is.

Het model dat is opgesteld door Lorenz is geen volledig realistische beschrijving van de atmosferische convectie, maar zijn onderzoek toont aan dat de bewegingen in de atmosfeer op langere termijn onvoorspelbaar zijn. Als meteoroog kon Lorenz zo een wetenschappelijk excuus geven voor het feit dat het zo moeilijk is om betrouwbare weersvoorspellingen te doen op langere termijn.

Een ander kenmerk van deze "vreemde attractoren" is dat hun vormen dikwijls fractaalvormen zijn. De grafische weergave vertoont dus zelfgelijkvormigheid op verschillende schaalgroottes.

Als we dieper zouden inzoomen op de Lorenz attractor, zou blijken dat het uit oneindig veel lagen bestaat.

 

Beta-attractoren zijn er dus in alle maten en vormen.

• Bij het systeem van de haaien en garnalen hadden we dus een vrij eenvoudige Beta-attractor, waarbij het eruitvoortvloeiende evolutiepatroon ook een duidelijke regelmaat vertoonde.
• Bij de Lorenz-attractor is het evolutiepatroon in bepaalde situaties chaotisch : er is geen regelmaat meer in te bespeuren. Nochtans vertoont de attractor zelf nog een mooie regelmatige vorm en symmetrie.
• Wanneer zowel in het evolutiepatroon, als de attractor alle regelmaat zoek zou zijn, bevinden we ons opnieuw in een "Boltzmaniaanse situatie" : er is geen informatie in het systeem, er is geen attractor en er is ten hoogste een gemiddelde symmetrie.

Deze 3 voorbeelden, een punt-attractor, de Lorenz-attractor en de afwezigheid van attractoren, tonen aan dat evolutiepatroon van zeer eenvoudig, tot zeer complex kunnen zijn. De bijdrage van terugkoppeling (zelfreferentie) tot deze complexiteit is hierbij vaak hoog. Deze terugkoppeling is echter ook verantwoordelijk voor de tijdelijke stabilisatie van de systemen in bepaalde omstandigheden.

 

Het bestaan en de visualisatie van ingewikkelde attractoren is slechts mogelijk met goede computersystemen, die de nodige simulaties kunnen uitvoeren. Op vele terreinen heeft men intussen al dergelijke complexe attractoren gevonden. Hierbij nog enkele voorbeelden uit deze "vreemde" wereld.

• populatiebiologie : de geremde groeifunctie
  De evolutie van bijvoorbeeld het aantal insecten in een populatie kan in een mathematische formule worden gegoten. In overeenstemming met het principe van de fluxmaximalisatie, zal de flux binnen de populatie toenemen (en dus de populatie toenemen), tot de draagkracht van de populatie in de omgeving is bereikt. De groei van de populatie is dus gelimiteerd.
  Deze limieten in de groeiende populatie zijn afhankelijk van :
  - het aantal individuen in de populatie = N
  - de bovenlimiet van de populatie = K
  - een factor die de groeisnelheid aangeeft = r
  De mathematische beschrijving van de populatiegroei is de volgende :
  
  dN/dt = r N ( (K-N) / K )
  
  Deze vergelijking is bekend als de "Lotka-Volterra vergelijking" of de "logistieke vergelijking", en is niet-lineair in zijn verloop. Een gemiddelde populatie groeit aanvankelijk exponentieel volgens de soortspecifieke factor r, totdat de beschikbaarheid van essentiële levensmiddelen beperkend wordt. De populatie stabiliseert zich op het niveau van de "draagkracht" K van de populatie.
  De term ( (K-N) / K ) geeft de negatieve feedback weer, wanneer de populatie zijn maximale niveau bereikt (niveau van quasi-evenwicht). De groeisnelheid van de populatie neemt toe, tot N een waarde gelijk aan K/2 bereikt, en valt dan geleidelijk aan tot 0, bij de waarde van de asymptoot.
  De factor r gaat ervan uit dat de populatiegroei enkel beperkt is door de geboorte en sterftewaarden.
  De factor K daarentegen (of (K-N) / K ) geeft de weerstand van de omgeving weer,die toeneemt naarmate de draagkracht van de populatie wordt bereikt.
  Onder andere de groep onderzoekers van Prigogine heeft deze vergelijking uitgebreid onderzocht, en aangetoond dat naargelang de waarden van de verschillende parameters, verschillende toestanden van quasi-evenwicht en limietcycli worden bereikt.
  De vergelijking op zich is zo uitgebreid gebruikt, dat de "r" en de "K" tot het standaard jargon van de ecologen behoort. In de biologische evolutietheorie spreekt men van "r-selectie", wanneer een bepaalde biologisch soort is aangepast aan een groei in een omgeving met onbeperkte voeding, terwijl men van "K-selectie" spreekt als de soort is aangepast aan een ecologische niche met een beperkte groeimogelijkheden.
  Verdere studie van de r-soorten en K-soorten in de biologie, wijst erop dat deze twee klassen organismen verschillende eigenschappen ontwikkelen. R-geselecteerde soorten, zoals kikkers, produceren gewoonlijk een groot aantal kleine nakomelingen, en besteden weinig of geen aandacht aan het opvoeden of verdedigen ervan. K-geselecteerde soorten, zoals elanden, zouden een complexer gedrag ontwikkelen, met kenmerken zoals sociaal gedrag, met maximale aanpassing aan de ecologische niche. Ze produceren slechts een klein aantal grote jongen, maar investeren veel tijd en energie in de opvoeding van de jongen.
• chemische klokken
  Wanneer we bepaalde chemische stoffen bij elkaar voegen, ontstaan er bij bepaalde toevoersnelheden kleurreacties, waarbij de ganse vloeistof van een afwisselend patroon van rood en blauw vertoont. Dit betekent de miljarden molecules tegelijkertijd nieuwe chemische bindingen aangaan -en de blauwe kleur vertonen - om enkele ogenblikken later weer omgevormd te worden tot de rode moleculaire vorm. Omwille van het oscillerende patroon spreekt men van chemische klokken.
• het weer
  Het gedrag van de aardse atmosfeer wordt bepaald door de evolutie van tal van variabele factoren zoals de wind, de temperatuur, de luchtdruk enzovoort. Deze variabelen evolueren niet louter toevallig, maar vertonen een min of meer regelmatig patroon. Dit patroon kan weergegeven worden door een mathematisch model, dat complexer is dan bijvoorbeeld het Lorenz-model dat we eerder hebben gezien. Door de grote complexiteit is de voorspelling op lange termijn is zeer moeilijk, omdat een kleine variatie van de begincondities, tot tal van verschillende evolutiepatronen kan leiden. De weerman heeft dus inderdaad een goed excuus bij faling van zijn voorspellingen.
• het zonnestelsel
  Voor de menselijke waarnemer lijken de bewegingen van de planeten rond de zon een perfecte regelmaat te vertonen. Op langere termijn echter blijkt ook dit een misvatting. De evolutiepatronen van de sommige kometen, asteroïden en zelfs planeten zijn ook op langere termijn niet voorspelbaar.
  Het zijn dus niet enkel de eenvoudige Alfa-attractoren die met mathematische zekerheid de evolutie van ons zonnestelsels bepalen. Het geheel van interacties tussen de kometen, planeten en de zon is een complex dynamisch proces, dat gezamelijk te beschouwen is als een stelsel Beta-attractoren.
• beursevoluties
  Op het eerste zicht lijken beursevoluties een volkomen onregelmatig patroon te vertonen. Ook in de beursevoluties slaagt men erin door mathematische analyse attractoren te vinden, die het gedrag op langere termijn lijken te beïnvloeden.
  De gevoeligheid voor heel kleine factoren, maakt ook hier echter dat voorspelbaarheid op langere termijn nauwelijks mogelijk is. Waar zogenaamde beursgoeroe’s hun wetenschappelijke onderbouw halen om voorpellingen op lange termijn te doen, is dan ook een wetenschappelijk raadsel.

 

De complexiteit van deze systemen is dus veel hoger dan de eenvoudige deterministische systemen die door Newton en Hooke zijn beschreven. Mathematische beschrijvingen van deze complexe Beta-systemen zijn er dan ook pas gekomen met de ontwikkeling van krachtige computers, van zodra de computerkracht voldoende hoog was om redelijke simulaties te maken van het gedrag van deze complexe systemen.

Terug naar de index van dit hoofdstuk

 

5. VORMING VAN COMPLEXE CYCLI EN HYPERCYCLI

In de voorgaande paragrafen is het duidelijk geworden, dat koppeling - en in het bijzonder terugkoppeling - een uiterst belangrijk principe is in de evolutie. Het verhoogt de rijkdom aan patronen die we rondom ons kunnen zien heel drastisch, en zelf hebben we als levende wezens ons bestaan te danken aan een zeer ingewikkeld complex van stromen van materie, energie en informatie, op velerlei wijzen met elkaar interagerend en gekoppeld.

Hierbij kan een onbeperkt aantal Beta-attractoren ontstaan, gaande van zeer éénvoudig tot zeer complex. We merken echter dat wanneer de Beta-attractoren zeer complex zijn, ook het evolutiepatroon zeer complex wordt, en in sommige gevallen chaotisch.

Daarom moeten we ons afvragen hoe zeer complexe stromen in de evolutie, toch nog een grote mate van ordening kunnen vertonen. Hieruit zal blijken dat koppeling van de opwaartse en neerwaartse stroom belangrijk zijn, doch dat naast het principe van terugkoppeling, ook de wijze van kanalisatie cruciaal is voor een gecontroleerd verloop van een complexe evolutiestroom.

Het principe van de koppeling en de kanalisatie, spelen dus een virtuoos samenspel in de evolutie, dat essentieel is voor het onstaan en handhaven van complexe systemen.

Terug naar de index van dit hoofdstuk

5.1. Kanalisatie versus kanabilisatie van de opwaartse stroom

Om het samenspel tussen koppeling en kanalisatie te verduidelijken, zullen we opnieuw vertrekken van een éénvoudig voorbeeld uit de chemie. We zullen zien dat een gepaste "kanalisatie" ervoor moet zorgen dat de neerwaartse stroom zo goed mogelijk gekoppeld wordt met de opwaartse stroom.

We zullen hier het voorbeeld van een electrische batterij nemen. In een electrische batterij, worden chemische reacties gekoppeld. Door een goede kanalisatie, kunnen we hieruit een electrische stroom verkrijgen, die we bijvoorbeeld kunnen gebruiken voor het aandrijven van een electrische motor. Een electrochemische batterij kan gebruikt worden om in een bepaald systeem "orde te importeren", waardoor binnen het betrokken systeem de entropie kan verlagen. We zullen ons hier echter beperken tot de werking van de batterij zelf, om de mechanismen van koppeling en kanalisatie te verduidelijken.

In onderstaande figuur is het voorbeeld van een loodbatterij gegeven, die bijvoorbeeld in een auto kan worden gebruikt.

Fig H6F13 : een electrochemische cel zonder (links) en met (rechts) kanalisatie van de electronenstroom

In een dergelijke batterij, worden platen van lood (Pb) en looddioxide (PbO₂), geplaatst in een oplossing van zwavelzuur (H₂SO₄). In water zal de zwavelzuur splitsten in zijn ionen H+ en SO42-. In aanwezigheid van zwavelzuurionen, heeft het lood de spontane eigenschap electronen af te staan en loodsulfaat (PbSO4) te vormen. Het looddioxide daarentegen, heeft de eigenschap spontaan electronen op te nemen, en eveneens loodsulfaat te vormen.

• Koppeling van 2 reacties (figuur H6F13a)

Door de plaatsing van beide types metalen (lood en looddioxide), in één en dezelfde oplossing met zwavelzuur, worden de spontane reacties aan elkaar gekoppeld. De electronen die door het lood worden afgegeven, worden door het looddioxide opgenomen. Het zijn dus perfecte partners. Deze reactie zou doorgaan tot al het lood is omgevormd tot looddioxide.

• Koppeling én kanalisatie van 2 reacties (Figuur H6F13b)

Wanneer we nu de 2 plaatjes niet enkel samen in een oplossing brengen, doch bovendien met elkaar verbinden door een koperen draadje aan beide metalen vast te hechten, zal de uitwisseling van electronen preferentieel via de koperdraad gebeuren.

We hebben de electrische stroom gekanaliseerd.

De miljoenen electronen stromen nu niet meer kris-kras door het water heen, waarbij ze continu botsen met de stuurloze watermolecules, doch ze kiezen voornamelijk voor de "snelweg" die hen wordt aangeboden (de koperdraad). Hierdoor stromen ze "in formatie" : het is een ge-informeerde beweging. Zoals we weten uit het vorige hoofdstuk, is een geïnformeerde beweging noodzakelijk om "arbeid" te kunnen verrichten. Deze electrische arbeid kunnen we gebruiken om een opwaartse stroom te veroorzaken, en bijvoorbeeld een electrische motor te laten draaien, of de lichten van een auto te laten branden. Zonder deze kanalisatie, zouden we "korstluiting" krijgen van de electrische stroom.

Niet enkel de koppeling, maar ook de kanalisatie, en de wijze van waarop deze gebeuren zijn dus cruciaal voor het mogelijk maken van de opwaartse stroom.

Indien de stroom die ontstaat door koppeling niet wordt gekanaliseerd, zal de geïnformeerde beweging te snel worden verspreid, en kunnen we geen of slechts een beperkte opwaartse stroom veroorzaken. De neerwaartse stroom "kanabiliseert zichzelf" als we hem niet kanaliseren.

Terug naar de index van dit hoofdstuk

 

5.2. Complexe cycli en hypercycli in de natuur

Het bovenstaande voorbeeld van koppeling en kanalisatie was het resultaat van het menselijk vernuft.

In de natuur ontstaan gedurende de evolutie zowel spontane kanalisaties als spontane koppelingen, die mettertijd met elkaar gaan interageren en zo het bestaan van dissipatieve structuren bevorderen en in stand houden.

De mooiste voorbeelden hiervan zijn levende wezens : dit zijn ware kunstwerken van koppelingen en kanalisaties, die de neerwaartse stroom ertoe dwingen om een ingewikkelde weg te volgen vooraleer zijn eindbestemming te bereiken, namelijk de complete verspreiding. Door de tijdsvertraging die de stroom van M/E/I ondergaat, kunnen geïnformeerde structuren en processen ontstaan.

Stap voor stap zullen we beschrijven hoe de stromen van materie, energie en informatie hun impact op de neerwaartse stroom verhogen, door het benutten van ingenieuze koppelingen en kanalisaties. Hierdoor ontstaan niet enkel complexe cycli, doch ook cycli die op hun beurt zijn samengesteld uit verschillende cycli : dit zijn de hypercycli. Dit beschouwen we als het hoogste emergente niveau van de Beta-processen. Zo komen we tot de drie niveau’s van Beta-processen die we voorstelden :
- de kanalisaties
- de cycli
- de hypercycli

In de natuur die we op aarde aantreffen, worden vele levende wezens van energie voorzien door een aaneenschakeling van natuurlijke electrochemische cellen.

Zo bevatten bijvoorbeeld alle planten chlorofyl in de bladeren. Dit chlorofyl heeft een groene kleur, omdat het alle golflengten van het zichtbaar spectrum absorbeert (rood, blauw), doch vrijwel al de groene en gele straling weerkaatst. Deze groene kleur wordt zichtbaar voor de mens, met als resultaat dat we alle chlorofylhoudende delen van planten als groen aanzien. In dit chlorofyl wordt - door een reeks opeenvolgende electrochemische reacties - de energie van het zonnelicht als "neerwaartse stroom" gebruikt om een "opwaarste stroom" te voeden. Deze opwaarste stroom wordt de "fotosynthese" genoemd, omdat de synthese van energierijke organische molecules wordt bekomen door het gebruik van zonnestralen. Deze energie wordt door de plant gebruikt om alle energieverslindende reacties van brandstof te voorzien, of om de energie op te slaan onder vorm van koolhydraten zoals fructose en glucose. Om dit laatste te kunnen verwezenlijken, gebruikt de plant water en CO₂ (koolstofdioxide uit de lucht). Bij de fotosynthese zelf wordt zuurstof gevormd ; dit is -zoals reeds eerder vermeld - de oorzaak van het voorkomen van zuurstof in onze aardatmosfeer. Typerend voor het uiterst delicate evenwicht in deze biochemische processen is dat de plant ook zuurstof gebruikt om glucose af te breken tot meer "liquide" energiebronnen. Met deze zuurstof moet echter voorzichtig worden omgesprongen, omdat ironisch genoeg, hoge concentraties zuurstof toxisch zijn voor de cel.

Al bij al is deze fotosynthese uiterste belangrijk voor veel levende wezens op aarde. Planten zijn autotroof, en zijn in staat om -door gebruik van zonlicht en CO_{2 -} volledig in hun M/E behoefte te voorzien. Alle dieren echter zijn heterotroof, en moeten zich voeden met planten of andere dieren om hun M/E behoefte te voldoen.

Het belang van de koppeling van een "opwaartse" met een "neerwaartse" stroom in de biochemie werd uitvoerig uiteengezet door Willard Gibbs (1839-1903). Gibbs paste de principes die Boltzmann had ontdekt voor de thermodynamica, toe op de biochemie. Hij voerde hiervoor het begrip "vrije energie" in. De meeste biochemische reacties in levende planten of dieren zijn reacties die niet spontaan verlopen, omdat ze van een minder geordende naar een meer geordende toestand verlopen : de meeste reacties moeten immers mee de immense ordening in een biologisch wezen mee helpen instandhouden. Deze immense beperking van de verspreiding die in een levend wezen plaatsgrijpt, kan enkel doorgaan indien buiten een nog grotere verspreiding wordt ge-exporteerd naar de omgeving. Dit impliceert dat elke chemische reactie in het levend wezen, voor een gedeelte bijdraagt aan het creëren van interne orde, en voor een ander gedeelte aan externe verspreiding ; met andere woorden, voor een gedeelte aan het leveren van interne arbeid (energieflux), en voor een gedeelte aan het produceren van warmte, die uiteindelijk wordt afgegeven aan de omgeving. Van alle voeding die een levend wezen opneemt, kan het dus een gedeelte vrij gebruiken om zijn interne orde te handhaven, doch er dient steeds een deel "tol" betaald te worden, onder de vorm van warmte. Dit vrije gedeelte van de energie noemde Gibbs dan ook de "vrije energie". Het is het gedeelte van de energie, dat kan gebruikt worden als energiebron voor de "opwaartse" stroom. Gibbs is erin geslaagd een kwantitatieve benadering voor deze vrije energie uit te denken, zodat voor elke individuele biochemische reactie, deze vrije energie kan worden berekend. Elk levend wezen neemt met zijn voeding een grote hoeveelheid vrije energie op. Gedurende de afbraak in het het lichaam en de cellen, wordt deze vrije energie gebruikt voor het mogelijk maken van levensnoodzakelijke processen. Door deze geleidelijke biochemische afbraak, blijft er van de voeding uiteindelijk nog slechts een gedeelte over, waar geen vrije energie meer uit te bekomen is. Deze "afval" moet dan ook verwijderd worden.

Naast de reeds vermelde fotosynthese, die indirect voor de energievoorziening van alle levende wezens van groot belang is, is ook de glycolyse, of de ‘splitsing van glucose’ van een evenwaardig belang. Het is immers de eerste stap in het energiemetabolisme van vrjwel alle levende wezens. Gedurende deze glycolyse, wordt de energierijke glucose molecule (die zes koolstofatomen bevat), gesplitst in 2 molecules pyruvaat. Dit gebeurt in een cascade van 9 biochemische reacties. Deze chemische reacties gebeuren in de mitochondriën, dit zijn celorganellen die beschouwd kunnen worden als de energiecentrales van de levende cellen. In deze energiecentrales is de koppeling en kanalisatie, door de geleidelijke evolutie, uiterst gesofisticeerd geworden. Elk van de 9 chemische reacties is te beschouwen als een electrochemische cel, en de 9 electrochemische cellen zijn onderling met elkaar gekoppeld, waardoor ze een electronenstroom veroorzaken, die loopt van een "top van een vrije-energieberg", naar een dal. In 4 van deze reacties wordt voldoende arbeid verricht om een andere energierijke molecule (ATP) te vormen. In 2 reacties wordt echter telkens 1 ATP-molecules gebruikt, waardoor er een netto-aanwinst is van 2 ATP molecules. (De ATP molecules zijn de "universele brandstof" van de biochemie.)

Kenmerkend aan de glycolyse is dat de concentraties op en neer gaan in functie van de tijd : de glycolyse is dus te beschouwen als een natuurlijke chemische klok. Het glycolyseproces is inderdaad een proces dat ver van de evenwichtssituatie plaatsgrijpt, en dit wordt mogelijk gemaakt door enerzijds de energietoevoer en anderzijds de complexe regulatiemechanismen. Indien er bijvoorbeeld veel ATP in de cel voorhanden is, zal een terugkoppelingsmechanisme ervoor zorgen dat de glucose trager wordt afgebroken ; omgekeerd wijst de aanwezigheid van veel ADP (de precursor en het eerste afbraakproduct van ATP) op een hoog energieverbruik, en leidt dit tot een versnelling van de glucose-afbraak. Veel energieprocessen in de levende cellen, en ook processen die afhankelijk zijn van ATP, worden beïnvloed door deze "glycolytische trilling". Het is dan ook één van de belangrijkste "Beta-processen" in de levende cel.

Levende organismen bevatten diverse biochemische cycli, die bovendien met elkaar gekoppeld zijn, waardoor ze hypercycli vormen. Ook in de ecologie en economie spelen deze cycli en hypercycli een belangrijke rol in de "homeostase" van het systeem.

Omwille van het belang hiervan, zullen we ook in het volgend hoofstuk een voorbeeld geven van het onstaan van hypercycli, die essentieel zijn geweest voor het onstaan van de Gamma-attractoren en Gamma-informatie in de natuur.

Terug naar de index van dit hoofdstuk

 

6. CONCLUSIE

In dit hoofdstuk werd aangetoond dat de complexere processen die we op onze aarde waarnemen, en die ook voor de gemiddelde evolutie kenmerkend zijn, veelal het gevolg zijn van wat ik "Beta-attractoren" heb genoemd. De complexe organisatie van deze processen is het gevolg van informatie die eigen is aan het proces zelf, en die het gevolg is van interacties in het proces.

Deze processen kunnen enkel ontstaan en blijven bestaan, indien ze worden gevoed door een passende stroom van materie, energie en informatie ; indien dit inderdaad het geval is, zullen ze zelf groeien (en hun flux maximaliseren) tot hun ultieme vorm en functie, in evenwicht met de draagkracht van de omgeving. Om die reden worden ze zelfvoedende of zelforganiserende processen genoemd.

Deze voeding is nodig om de spontane trend naar verspreiding te kunnen tegengaan.

Naast deze koppeling met een relatief sterk coherente stroom (met andere woorden de voeding), bevatten deze Beta-organisaties veelal nog een aantal kenmerken die de complexiteit sterk kunnen doen toenemen. Zo komen we tot de drie niveau’s van Beta-processen die we voorstelden :
- de kanalisaties
- de cycli
- de hypercycli

De aard van de Beta-attractoren kan variëren van éénvoudige puntattractoren, tot "vreemde attractoren", die aan de basis liggen van zeer complexe en nauwelijks voorspelbare evolutiepatronen. We treffen dus zowel universele Beta-attractoren aan, die we in de gemiddelde evolutie met hoge frequentie kunnen verwachten, als eerder sporadisch voorkomende Beta-attractoren.

Omwille van hun complexiteit is het gedrag van interacties ten gevolge van Beta-attractoren veel moeilijker mathematisch te kwantificeren dan het gedrag van Alfa-attractoren. Ze zijn daarom echter niet minder belangrijk.

De Beta-attractoren verrijken het "semiotische landschap" met een nog grotere diversiteit dan de basis die gelegd was door de Alfa-attractoren. Daar waar de Alfa-attractoren in belangrijke mate de coherente van het semiotisch landschap verhogen, dragen de Beta-attractoren in belangrijke mate bij tot de verhoging van de complexiteit ervan.

Onderstaande figuur situeert nogmaals de plaats van de Beta-interacties in de "gemiddelde evolutie".

Figuur HXfX : "de gemiddelde evolutie"

Terug naar de index van dit hoofdstuk

---