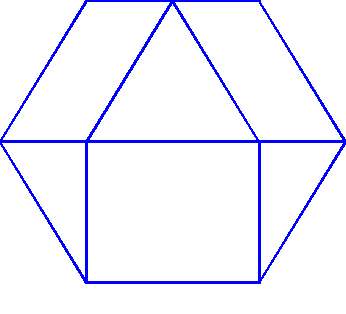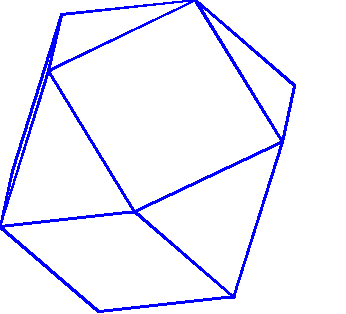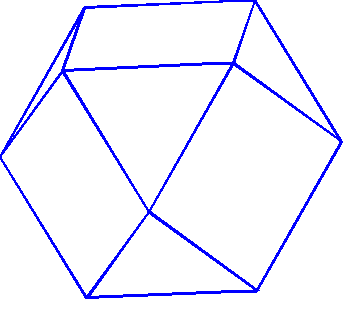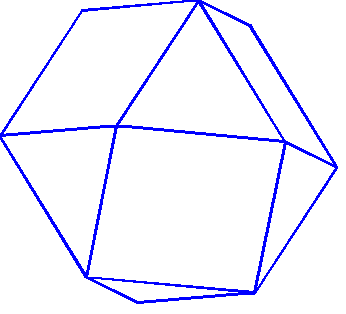
The accepted name for the entity in question is truncated octahedron because if you cleave the tetrahedral points off an octahedron, your entity is what remainsSounds good to me, Chris :-)
Let's see...the simplest three dimensional figure has four sides
(tetrahedron) Then there's the five sided pyramid and the six
sided cube and let's not forget Buckminster Fuller's most
fundamental geodesic dome the isooctahedron with it's eight
equilateral interlocking triangles. What's so special about a geodesic dome anyhow? We have all
seen numerous applications of geodesic dome technology. Wherever
expansive ceilings unencumbered by support columns are called
for you'll find geodesic domes. The strength of arched
interlocking triangles is phenomenal. I expect the twenty first
century will find many more applications for this architectural
breakthrough.
I had hoped to apply geodesic dome technology to my first
hexagonal house, but when I realized that thirty triangles would
be necessary to build a symmetrical base on a six sided figure I
lost interest. You see, geodesic dome technology requires a base
multiple of 5. Pentagons (1 x 5) and decagons (2 x 5)are fine. Since
hexagons have six sides a minimum of thirty (6 x 5) triangles would be
required on the base alone. Instead I built two layers of
interlocking right triangles and equilateral triangles on the
hexagonal base but wasn't really satisfied with the result. The quadradecahedron
was designed to solve this
problem. I'll have an animated illustration of this up soon and
I'll also be discussing hexagonal housing and the Myterious Power of Six :-)
