Chapters 1 - 4 Study Guide Chapters 8 - 11 Study Guide Wadsworth's Astronomy Home Page


Introductory Astronomy: Study Guide
for Michael A. Seeds, "Foundations of Astronomy" Fourth Edition (1997)

Copyright © 1996 Heather L. Preston and Derek L. Buzasi


Study Guide for Seeds text, Chapters 5 - 7

You can check out some sample questions on these topics. Use them as flash cards, or tests of your reading comprehension. The multiple choice questions on the exam are mostly variants of these questions (but with a lot of plausible-sounding distractors -- read carefully!)
if you load your images a nice continuous spectrum (rainbow) will quickly appear here


Chapters 5 - 7: Newton's Laws through Light, Atoms, and Spectra

This summary does not take the place of reading the text or attending lectures, but it does provide supplemental information, summaries, and alternative explanations. Ummm, and it's shorter than rereading the text the night before a test!

Use the book and your notes to fill in wherever you are having trouble with understanding something -- and ask your instructor questions! :-)


Chapter 5 -- Newton's Laws, to Einstein

Galileo -- Early Experiments in Gravity

Newton -- Born Dec 25, 1642 and Jan 4, 1643 (see text pg. 77) -- published Principia in 1687. This book had an immense effect on physics and astronomy, and it predicted the theoretical existence of Neptune and Pluto, hitherto undiscovered planets.

Newton's Three Laws of Motion:

The first law is true because a moving object has momentum (mass x velocity). Something slow and massive (satellite in space, docking ship) is just as dangerous to get in the way of as something fast and light (speeding bullet!). Mass is not the same as weight (which depends on the local strength of gravity). Mass is an innate characteristic of any hunk of matter. Velocity is a "directed rate of motion" -- that is, speed in a specific direction. If you change the speed or the direction, you are changing the velocity, and that would be an acceleration.

Newton's Law of Mutual Gravitation: Fgrav=GMm/(R2)
This means that the force of gravity between any two bodies is equal to a constant (the Gravitational Constant, G=6.67x10-11 N-m2/kg2) times the product of the masses of the two bodies in question, divided by the square of the distance between their centers (centers of mass, actually). A very important law, and the most general form of a gravity law. (G can also be expressed as: 6.67x10-11 m3/kg- sec2). In calculating, use units of G with Newtons if Force is in the equation, otherwise, use the non-Newtons units! On Earth's surface, we do the multiplication of G, using Earth's mass for M, and Earth's radius for R, and come up with an equation, F=mg, which describes the gravitational force at the surface of Earth (only!). g is called our gravitational acceleration, and g=9.8 m/sec2 .

Force is expressed in Newtons. A Newton is one kg-m/sec2 . You can remember this by thinking of F=ma, since m is mass in kg and a is acceleration in m/sec2 .

Energy is Force x Distance. It is expressed in N-m, which are also called Joules (abbreviated "J"). One Joule is also equal to one kg-m2/sec2. To remember that, think of the equation E=mc2 (Einstein's equation). We will actually use it in the not-too-distant future. "c" is a velocity, therefore c is in m/sec and mc2 must be kg-m2/sec2. There is kinetic energy (energy of motion) and potential energy (energy in a gravitational field or chemical bond, for example).
The equation for kinetic energy is: E=mv2/2
 The equation for gravitational potential energy is: E=GMm/R (just gravity's Force times the distance R!) Again, on Earth's surface this becomes E=mgh (where h is height above ground).

Orbits:

Circular Velocity is the rate at which an object would move in a circular orbit around a given massive body (like a satellite around the Moon, a planet around the Sun, or a baseball around an asteroid!). The equation for circular velocity is: Vcir= (GM/R)1/2

Escape Velocity is the velocity an object (of ANY mass) must have to leave the gravitational field of a massive body. There is an escape velocity from the Earth's surface, from the Sun's surface, even from the solar system, although that depends on how far you are from the Sun. The equation for escape velocity is:
Vesc = (2GM/R)1/2

In these two velocity equations, G is the gravitational constant (no Newtons!), M is the mass of the massive body, R is the distance between the massive body and the less massive object. Notice that escape velocity is equal to circular velocity times the square root of 2.

As you know from Kepler's first law, orbits are elliptical. The point at which an orbiting body is closest to the Earth is its perigee, the farthest-away point is its apogee. For orbits around the Sun, the corresponding points are perihelion and aphelion.

Angular Momentum is the product of a planet's mass, velocity (in its orbit) and distance from the Sun. The formula is simple: Ang. Mom. = mVR. It is always the same for a given body (barring collisions!), so it is the reason for Kepler's Second Law (equal areas swept out) - if R decreases, V must increase correspondingly.

Einstein - born 1879 - published Special Relativity in 1905, General Relativity in 1916. Special Relativity: Works for all kinds of electromagnetic phenomena, and for normal particles and so forth. E=mc2 comes from this theory, which means that a particle gains effective mass as it moves faster. This is called its relativistic mass, and it only gets large near the speed of light. This theory is also responsible for nifty things like time dilation and length contraction.
Two Postulates:

General Relativity: Ties Gravity in with the electromagnetic phenomena covered by special relativity. The Equivalence Principle: Observers cannot distinguish locally between inertial forces due to acceleration and uniform gravitational forces due to the presence of a massive body. So constant acceleration and gravity are indistinguishable.

In G.R., gravity can be considered as a curvature of space. This was tested and confirmed by the expedition that observed the total solar eclipse in May, 1919. They determined that starlight was indeed deflected by the Sun's gravity.



Chapter 6 -- Light and Telescopes

Light is made up of photons: particles of pure energy that have characteristics of both a particle and a wave. Light is a form of electromagnetic radiation, which encompasses everything from gamma rays (the highest energy, shortest wavelength photons) through X-rays, Ultraviolet (UV) radiation, the blue through red visible regions of the spectrum (visible light), Infrared (IR), Microwave, and short-wavelength (high frequency) radio waves such as UHF, VHF, FM and AM bands. ROYGBIV "Roy G. Biv" is the order of the colors of visible light from longest wavelength (Red) to shortest (Violet): Red Orange Yellow Green Blue Indigo Violet. The reddest wavelengths you can see easily are around 700 nm (7x10-7 meters), and green is around 530 nm, while the shortest wavelengths you can see are near 400 nm (4x10-7 meters).

Photon energies: the Longer the wavelength, the Lower the frequency, the Lower the energy of the photon. Conversely, the shorter the wavelength, the higher the frequency, the higher the energy of the photon! The relationship between frequency and wavelength is inverse: that is, high numbers for frequency mean low numbers for (short!) wavelength. That relation is mathematically precise:
f l = c
where f is the frequency, l is the wavelength, and c=3x108m/sec is the speed of light (always the same, in vacuum).
The energy of the photon is expressed in terms just as precise. It increases directly with frequency, so it decreases as wavelength gets longer. For completeness, Here is the equation for the energy of a photon: E = h f
We could also write this (realizing that f = c/l ) as: E = hc/l .
In this equation, h=6.626x10-34 J. It is a constant, known as "Planck's constant." This is NOT spelled out in your book!

Atmosphere's effect: The atmosphere absorbs and/or reflects large portions of the electromagnetic spectrum, so that only a few narrow "windows" are relatively unaffected, so that the photons make it all the way to the surface, where we can observe them! You know about the ozone layer absorbing the UV rays that would otherwise cause us to get bad sunburns and skin cancer. IR is absorbed fairly low in the atmosphere, by water vapor molecules, so it's possible to get above that level and observe stars in the IR -- one reason why telescopes are on mountaintops! Another reason is "poor seeing" -- the blurring of an image on a photographic plate or detector due to atmospheric turbulence making the image appear to jump and dance.

Even blue visible light interacts with the atmosphere a little -- it is scattered by the water molecules in the atmosphere so that the sunlight that reaches us appears slightly less blue than it would seen from space, and the sky, which is scattering the blue light in all sorts of random directions, appears blue. You know it's not intrinsically BLUE because at night you see the stars, fireworks, and all sorts of other things in their normal colors. At night, in the Earth's shadow, the sunlight is blocked so the atmosphere can't scatter it and appear blue. On the surface of an airless body, such as an asteroid or the moon or the planet Mercury, light of every wavelength could be detected with the appropriate instruments, and there would be no "seeing" effects to blur the images.

Telescopes: An Intro to Optics

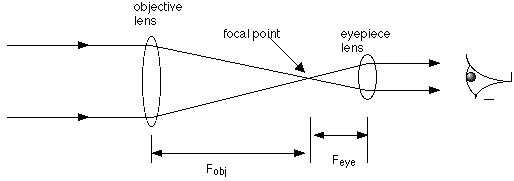
This is a diagram of a refracting telescope. Notice the focal length of the objective lens, Fobj. The objective lens brings the light to a focus at the point that is one focal length away from the lens, and the eyepiece lens must then be placed in such a way that its focal point coincides with the focal point of the objective lens. It has a certain focal length, due to its curvature, and it must be placed exactly one Feye distance from the focal point of the objective lens (for example, if Feye is 3 cm, the eyepice lens must be 3 cm from the objective lens' focal point. If Fobj is 20 cm, then that means the eyepiece lens must be 23 cm from the objective lens, along the same axis). Light rays enter parallel to one another and must leave parallel as well!

The magnification attained by a telescope is the ratio of the objective to the eyepiece focal lengths: Magnification= Fobj/Feye .

The resolving power of a telescope should ideally be a very small number. It tells you how close together two things can appear (in angular separation on the sky) before they blur together and can no longer be seen as distinct from one another (resolved). Here's the general equation: Resolving power = " a " = 206,265 l /D, where D is the diameter of the telescope, and l is the wavelength of the light in the same units (for instance, cm). For visible light at a mean wavelength of around 560 nm (= 5.6x10-5cm) we get: a = 206,265x(5.6x10-5cm) / D = 11.6/D where D is in cm.

One serious problem with refracting telescopes is chromatic aberration, which looks like colored haloes around the images when you see it through an eyepiece. It occurs because blue light is bent more as it travels through the lenses than red light is, so it focuses closer to the objective lens than the red light does. Every color in between is of course focusing at a slightly different place as well. You can construct an achromatic lens that will focus two specific wavelengths at the same place (it's two lenses ground of different materials and fitting together exactly), but this is expensive, requiring four very precise optical surfaces to be ground. Other drawbacks of refracting telescopes are listed in your HW solution set for CH5&6!

Reflecting Telescopes: Here is a diagram of a reflecting telescope. What kind of reflecting telescope is it: prime focus, Newtonian, Cassegrain, or Schmidt-Cassegrain?

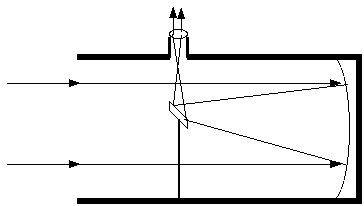
A concave mirror, called the objective (or primary) mirror, is ground with a parabolic curve (not a spherical curve, which is easier to make but which doesn't focus the light perfectly -- a condition called spherical aberration), so that parallel rays of light entering it will come to a focus at the focal point of the paraboloid, called the prime focus. Some telescopes stop there, and a camera or detector is placed at the prime focus. Newton had a design that incorporated a small flat mirror at a 45-degree angle to the axis of the telescope, which would reflect the nearly-focussed light off to the side of the tube, where a convenient eyepiece could be placed. Larger-diameter amateur telescopes are often Newtonian reflectors. Not to be outdone, Cassegrain invented a clever arrangement, with a hole in the exact center of the primary mirror, and a reflecting secondary mirror that directs the nearly-focussed beam down through the hole in the back of the telescope, with an eyepiece or other detector attached behind the primary mirror. A thin lens called a Schmidt corrector plate can be added to correct for off-axis and spherical aberration, and that is frequently added to midsize amateur telescopes with a Cassegrain focus --thus the telescope is known as a Schmidt-Cassegrain telescope. This is a kind often used in intro astronomy labs!

Light-Gathering Power: telescope comparisons: The light-gathering power of one telescope compared to another is simply the ratio of the surface areas of their mirrors or lenses. It can be expressed with this equation:
LGPA/LGPB = DA/DB
where DA and DB are the diameters of telescopes "A" and "B," respectively.

Active optics: "floppy" mirrors and multi-mirror telescopes. The computer controls the curve of the surface.

Adaptive optics: A way to defeat the effects of poor "seeing." Computer examines the "dance" of the image and predicts where it will go next, then moves the optics to compensate for the predicted change in position on the detector.

Imaging Systems: The most popular imaging medium with astronomers until the late 70's/early 80's was photographic plates, because of their long-term stability (like CDs versus cassette tapes). These were glass; you can imagine the drawbacks to this system. The most popular by far today is the CCD, or charge-coupled device. They can detect both bright and faint objects in the same exposure (hard to "saturate" them, which is easy with photographic plates). They are also much more sensitive than plates, and can be read directly into the computer (no hours squinting over an iris photometer!).

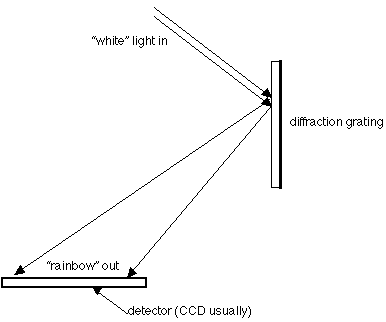
Spectrograph: Spreads the light out into its component colors. Spectrographs used to use prisms, but for a long time they've used gratings, which reflect the light and spread it out rather than passing it through glass, where some light can be "lost." Here's a schematic of a spectrograph:

Radio Telescopes: One dish doesn't usually give you very good resolution. You must have an aperture that is long compared to the wavelength being observed, so for typical radio wavelengths that means thousands of meters. Single radio dishes of that size would be hard to steer, etc. (The biggest one in the world - you saw it in the James Bond movie "Golden Eye" - is the big valley-mounted dish at Arecibo, P.R.. This dish is 300 meters across. It is not "steered" by moving the dish, but by changing the way the timing of incoming signals is treated electronically.) The Very Large Array (VLA) in Socorro, N.M., has a large number of midsize radio dishes mounted on train tracks, and these form an aperture of whatever size or shape is needed for the particular observation being made, using their combined signals in a technique called interferometry. An even larger aperture can be synthesized from telescopes located on separate continents, combining their received signals and timing information in what is called Very Long Baseline Interferometry. The resolution attainable by these coordinated radiotelescope efforts is a thousand times better than the resolution seen in good Earth-based optical-telescope images. Radio telescopes are great -- they can see in the daytime, they can see cold, dark matter (which optical telescopes can't since it doesn't glow in the visible wavelengths), they can see through thick dust clouds that scatter optical light and block our view of the galaxy's center. On the other hand, you have to do a lot of data-processing to get images!

Infrared Astronomy: As stated above, takes place mostly at altitude. Some at Mauna Kea, some in aircraft and some from the satellite IRAS (IR Astronomy Satellite).

Observatories that must fly:


Observatory that DOES fly:
The Hubble Space Telescope, on which I worked for five years, is a wondrous orbiting observatory with a variety of detectors and instruments, working at a variety of wavelengths (but mostly optical), and capable of imaging at impressively small resolutions, especially now that the Servicing Mission has corrected the flaw in the optical system.


Chapter 7: Starlight and Atoms

As you recall, temperature is the average kinetic energy of the atoms/molecules making up the thing being measured. Hot objects have faster-moving atoms or molecules. In hot gases, these are moving randomly and colliding with one another. In hot solids, the molecular bonds just vibrate faster and faster until the solid melts! Density will be related to the amount of heat you perceive from an object at a given temperature. That is, a really thin gas might be very high-temperature, but the number of molecules that actually hit your hand may be extremely small, so that the gas will not be able to "burn" you the way hot coffee (at a much lower temperature but higher density) would.

In science, we use the Kelvin temperature scale. It has no negative numbers. 0 degrees K is called absolute zero.

Here is a comparison between the Centigrade scale and the Kelvin scale. As you can see, the degrees are the same size, but the Kelvin scale has been offset so that 0 K is the point at which all atomic motion ceases. It has not been reached on Earth in any lab, although some labs are trying.

degrees Kelvin		degrees Centigrade
	0.			-273.2
	273.2			     0.		(water freezes)
	373.2			 100		(water boils)

Your body temperature is in there, around 340 K. If we turned off the lights, you could still be "seen" -- Q: in what wavelength region? Every opaque body -- solid, liquid, or even sufficiently dense gas -- gives off a continuum of radiation at a range of wavelengths, with the total brightness being characteristic of: 1) the temperature of the radiating body and 2) the size of the radiating body. The peak of the intensity occurs at a specific wavelength, lmax, which is characteristic of the temperature (in K). The exact relation is given by
Wien's Law: lmax = 3x106/T where T is in K and lmax comes out in nm. (Q: What would the units of the constant have to be?)

This thermal continuous radiation is also called a "blackbody" spectrum because an ideal "blackbody" is a perfect absorber and a perfect radiator (no impediment to the flow of energy in or out). As you can see from the equation, the higher the T, the shorter the lmax will be! So the bluer the peak wavelength of object's thermal spectrum, the hotter it is, and the brighter (for a given size). Why for a given size? Well, something very small but very bright per square centimeter, like a flashlight, will look much brighter up close than, say, a sandy beach with the sun shining. But if you back off a little, you realize that the total amount of light reflecting off the beach is a lot greater than the total amount of light coming from the flashlight, even if it ISN'T brighter per square centimeter. There are a lot more square centimeters on the beach than on the front "lens" of the flashlight. The beam of the flashlight is dwarfed by the aggregate light bouncing off the beach.

This brings us to another law, called the Stefan-Boltzmann Law: E = s T4 (J/sec-m2)
Here, E is the Energy (in Joules) being given off by a radiating body per second, per square meter.
The constant s = 5.67x10 -8 J/m2-sec-K is called the Stefan-Boltzmann constant. If you wanted the total brightness (Luminosity) of the object, you'd need to multiply this E by the surface area of the object! That's how the surface area comes into it (E is energy per sec per m2-- multiply by m2 to get energy/sec)

Summary for thermal continuous spectra -- Think: red-hot is hot (like an electric stove burner), but yellow-hot is hotter (flames), white-hot is hotter still, and blue-white, like a welder's torch, is REALLY hot! Also, the brightness per square meter increases like T to the fourth power (T4) -- increase T by a factor of 2, you'll increase the brightness by 16 times!

Atoms, and Spectra

A typical atom is Hydrogen (H). The Universe is made up of mostly H (90% by number of atoms), around 10% Helium (He), and the rest are trace elements (Carbon, Oxygen, Nitrogen, Gold, Iron, etc.). This goes for stars, too, then: 90% H, 10% He by number (composition has an effect on their spectra).

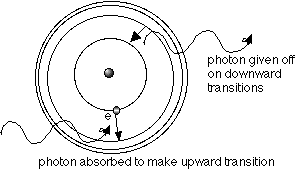
The H atom is the simplest. It consists of one proton being "orbited" by one electron. Change the number of protons, and you have a different chemical element -- the number of protons in the nucleus is what makes each unique. Each atom also has a unique set of allowed energy levels for the electron(s) to occupy. The spacing of the energy levels is like a signature for the atom. Here's a sample H atom:



If we added a neutron to the proton, we'd have an isotope of H known as Deuterium. Add another neutron and it's called Tritium. (A fourth neutron would fail to bind, it would decay into a proton and an electron, and you'd have Helium instead. That process is called fusion. We'll study it soon.)

The energy to get the electron from the n=1 level to the n=2 level is 10.2 eV (electon- volts, a tiny unit of energy. 1eV=1.6x10-19 Joules). If the H atom is near a source of many photons (for instance, a star), then the atom's electron can absorb a photon of exactly the energy it needs to make the jump up to an upper energy level. Think of an electron in a lower energy level as "wanting to travel." If the electron hitchikes from a lower energy level to a higher one, the atom is said to be "excited."

The energy needed to completely knock the electron free of the atom is 13.6 eV. If the electron gets free, the atom is said to be ionized.

Since the electron can ONLY move from one allowed energy level to another, it can only make jumps of very specific amounts of energy. If it's absorbing a photon to make that jump, the photons that can be absorbed are ONLY those with energies (therefore wavelengths and frequencies) corresponding to an allowed electron transition. So, if the electrons in the thin gas that is the outer layers of a star are using the photons coming out of the star to take their free rides to upper energy levels, those specific wavelengths will be missing from the resulting spectrum of the star: it will look like a comb with a few teeth missing. That is called an absorption spectrum.

If we're looking only at a thin, hot gas with nothing behind it in our line of sight, we will not see a thermal spectrum, and we will certainly not see an absorption spectrum. What will we see? The electron cannot stay in the upper levels forever. Eventually it will "fall" back down to the n=1 energy level, the ground state.When it does that, it has to give up the energy it's borrowed, and so it re-emits a photon of the exact wavelength corresponding to the amount of energy lost in the downward transition. That means that photons of exactly those wavelengths that were being absorbed will be re-emitted, but in a random direction, and only rarely into the original line of sight from which they were taken. Therefore, looking at the thin, hot gas, we see an emission spectrum.

Kirchoff's Laws Example: In the following diagram, what type of spectrum would each observer see?


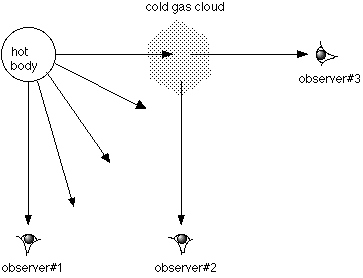
Spectrograph, again: As you look at the diagram of the spectrograph, you see that the starlight is spread out, and wherever the intensity would be low (not many photons), there is a dark line in an otherwise bright spectrum (see also: pg. 150 Fig 7-11). Those are called absorption lines. It's a different way of seeing the same absorption spectrum as above. If you were looking at an emission spectrum (a thin, hot gas with nothing behind it) the situation would be reversed: there would be mostly darkness, with a few bright lines of light at the specific wavelengths for the energy transitions in the atoms of the gas being examined. Those are called emission lines.

Since H and He and all the other elements have specific energy level spacings, which give them each their own "signature" absorption spectra, we can identify what elements are present in a star's atmosphere or in a hot, thin gas by looking at the pattern of wavelengths of the absorption or emission lines. In H, the dominant lines seen in the visible region are the Balmer lines. They all have the n=2 level as their starting point. The n=1 level lines are too far into the UV for us to see, naked-eye. So when astronomers started to characterize stellar absorption line spectra, they compared the "strength" of the H Balmer lines from one star to the next (that is, how deep and wide the Balmer lines were).

The Doppler Effect
When a light source is moving toward you, the light it emits is blueshifted (shortens wavelengths). When a light source is moving away from you, the light it emits is redshifted (lengthens wavelengths). That velocity toward you or away from you is called the star's radial velocity with respect to your position. If the star were moving perpendicular to your line of sight, that would be a transverse velocity, and there would be no Doppler shift detectable from it. Of course, most velocities of stars are at some in-between angle, so we only detect the radial component and must find other ways of measuring the transverse velocity. The amount of the shift is directly related to the original (unshifted) wavelength in the following way:

v/c=change in wavelength/original wavelength

This equation lets you calculate the velocity of the light source toward you or away from you. Simply look at the spectral lines and identify at what wavelengths they should be in the lab (from the pattern). Then for a given lab-wavelength (for example, a red line of 700 nm wavelength), measure the shift between that and the line you see in the (for example, redshifted) stellar spectrum. If in our example this shift were 7 nm, then the shifted line would show up at 707 nm on your spectrograph. Therefore, the speed of the source would be 7/700 times the speed of light, or 0.01c. That means the star would be moving away from you at 3x103 km/sec = 3,000 km/sec. Pretty fast! Note that you will only be able to determine this effect for absorption line and emission line spectra!, (That's because a thermal continuous spectrum doesn't have identifiable lines, so if the peak were shifted bluer, it would just look like the unshifted spectrum of a hotter star, right?)

Spectral Classification and "The Balmer Thermometer"
When astronomers started taking bunches of stellar spectra, they were just learning about what caused spectral lines. They noticed that the Balmer lines of hydrogen were very strong in some stars, and almost absent in others, but that they were the most consistently present at some strength (because stars are mostly hydrogen). They classified the ones with the deepest, strongest Balmer lines as type "A," next strongest type"B," and so forth right up to the type "O" stars, which have at best a little dip where the line should be.

As time went by, they discovered why the various spectra had the line strengths they had. It was a Goldilocks situation: if a star was too hot, almost all the H would be ionized, so there would be no electrons in the n=2 level to form Balmer lines by taking rides to other levels. If a star was too cold (2500 K is cold, for a star!) then there wouldn't be enough UV photons coming out of it to excite the electrons into the n=2 level from the ground state, so they couldn't hitchike to levels above n=2, either, they'd all be stuck in the ground state. A star that was "just right," an A- type star, has a temperature that allows the star's thermal continuous spectrum to give off just the right amount of UV to keep a lot of electrons hopping into the n=2 state, from which they absorb a variety of visisble-light photons to reach the various upper energy levels, forming strong Balmer absorption line. That's how the strength of the Balmer lines we observe in the stellar spectrum functions as a stellar thermometer.

When astronomers realized that the VERY hot and the VERY cool and the stars in-between could all have their temperatures measured in this way, they arranged the spectral types (A,B,C...) in order of temperature instead of line strength, and got: O, B, A, F, G, K, M. This was hard to remember, so their mnemonic (memory-device) for it was: "Oh, Be A Fine Girl, Kiss Me" -- Please feel free to come up with one that suits you better! Our sun is a G-type star, so at 5000 K it's cooler than the optimum temperature for forming deep Balmer lines.

Line broadening: When a star's surface is hot, that means the atoms in the star's "atmosphere" have a high average velocity. They can then absorb photons at a range of wavelengths very close to the one unique wavelength of a given energy transition, because the electron on a fast-moving H atom "sees" the photon slightly blueshifted or redshifted from its true wavelength. It makes the energy transition essentially using both the photon energy and the atom's own kinetic energy! This type of broadening is called Doppler broadening. There are other types of broadening of absorption or emission lines, one mentioned in your book is called collisional broadening. That occurs because in a high-density part of the star's atmosphere the atoms are so close together that they collide a lot, thus affecting their neighbors' energy level spacings. If such a collision occurs at the moment that a photon of the correct altered energy (wavelength) is passing by, it gets absorbed.



Sample Questions (do not turn in as HW, use to study for test!):