Kyberniidae

by Klaus F. Steiner (1994)

Kyberniidae demonstrates the dynamics of two mutually coupled oscillators, or in a more biological language: it simulates dueting males of the tropical katydid Mecopoda elongata L. The model is based only upon phase response curves and chirp cycle lengths.
The program uses experimental data I found in the process of my master thesis "Dynamik des Gesangs der Laubheuschrecke Mecopoda elongata L." (in English: "Dynamics of the calling song of the katydid Mecopoda elongata L."). Kyberniidae is a part of my thesis, too.
Kyberniidae is written in Borland Turbopascal 6.0 for DOS.

I have to apology, because Kyberniidae is not very user friendly, has no help system, is keyboard controlled (no mouse) and some manipulations are a little bit strange. And sometimes terminology within the program is inconsistent (e.g. synonyms are animal=Tier=system=oscillator). The reason is that the genesis of Kyberniidae was rather evolutionary than creational or logical.

Menu

Move menu cursor by pressing arrow keys and . Select with . Also you can make your selection by pressing the key corresponding to highlighted (red) letter in menu items name. Use to go back from submenu or graphic screen.

• Chorusing
  Coupling of two oscillators at which their endogenous chirp cycle lengths are constant. When you first time enter one of the following menu items you have to select the properties for the oscillators: for both you can choose between two items: New animal: a table (blue) will appear with data of my observed animals (no idea what I'm speaking about? Read Phase Response first). Select an animal with arrow keys and . Periodic: Constant rhythm, set circle length between 1000 and 4000 ms (cycle length is constant, the other oscillator can't influence this oscillator).
1. Phase-Coupling-Map    The ontogenetic oldest part of Kyberniidae. You may ignore it! For the sake of completeness: In the bottom left you can see the data describing the selected oscillators (Tier = animal; number: data from # animal; Tier C: constant rhythm). Over that you find their PRCs graphical coupled (PCM, phase coupling map). Figures "Attraction" show in which phases interactions will converge and how many cycles are needed at the most. In Figures "Entropy" you see reduction of Entropy from cycle to cycle (it depends on programs use of discrete PRCs that Entropy is greater zero sometimes although there is obviously just one globally stable fixpoint). Back to menu with .
2. PRCs + Poincaré Maps    This is a static graphic screen, too. Phase response curves of selected oscillators are shown. Under that you can see the Poincaré maps for both oscillators. A Poincaré map shows phase of the others chirp against phase of the others next chirp in animals chirp cycles.
3. Simulation    Realtime simulation of duetting animals. Two animals (yellow and blue) are drawn. Red thorax indicates that animal chirps, gray thorax that it's silent (see figure). Simultaneous the chirps are recorded in an oscillogram (color like singing animal). A gray "partition" wall between the animals separates them acoustically - by pressing the wall can be switched off and on (on=violett and off=gray line in oscillogram). Chirps can also be given as sound (press key 'S'), but don't do this on PC's other then 486-33, else sound is horrible! With keys '1' and '2' you can inactivate/activate the yellow (1) and blue (2) animal. 'p' pauses the simulation. Pressing 'r' clears the oscillogram (and trajectories if other digrams are displayed) but doesn't influence the animals' songs. Back to menu with 'Esc'.
4. Simulation + PCM    Like (3) but additionally with animated PCM (see 1). Trajectories will be drawn in PCM, fixpoints will be marked with a green circle (see Examples 1-3).
   
5. Sim + PRC + Poincaré    Like (3) but additionally with animated PRCs and Poincaré maps (see 2). Trajectories will be drawn in PRCs and Poincaré maps, fixpoints will be marked with green circles.
6. New oscillators    If you want to stay in submenu chorusing here you can select new oscillators. As described above but additional Don't change: the preselected oscillator stay the same.

• Bifurcation
  Coupling of two oscillators at which ratio between the endogenous chirp circle lengths is varied within a given interval. Like in "Chorusing" you have to select the animal's properties first, for second animal you have to define a range for endogenous chirp circle length and the width of steps within. The chirp cycle length are given in ratio between both animals (t...endogenous circle length of the animal indicated by index; indices: A..first selected, yellow animal, and B is the other one). For every step in this interval the phases in stationary states become computed.
1. Coupled Phases    The upper diagram on the left shows phases of blue's (the second one) chirps in yellow's chirp circles (see figure). Below the same diagram, but with reversed actors' part (see Example 4. Move cursor, the red vertical line, with arrow keys left and right (faster with ), then press - the PCM will occure. Key toggles between PCM and Poincaré maps.


2. Cycle Length    Instead phases in stable state the cycle length are displayed in the left diagrams. Everything else is like before.
3. Oscillator A    For the yellow animal (oscillator A) diagrams "phases" and "cycle length" are displayed.
4. Oscillator B    Like (3) but diagrams for blue animal.
5. New oscillators    You can select new animals and range of circle lengths.
• Quit    This closes program Kyberniidae

Some Examples

Some screenshots from Kyberniidae. More detailed descriptions and further examples of Kyberniidae will come soon.

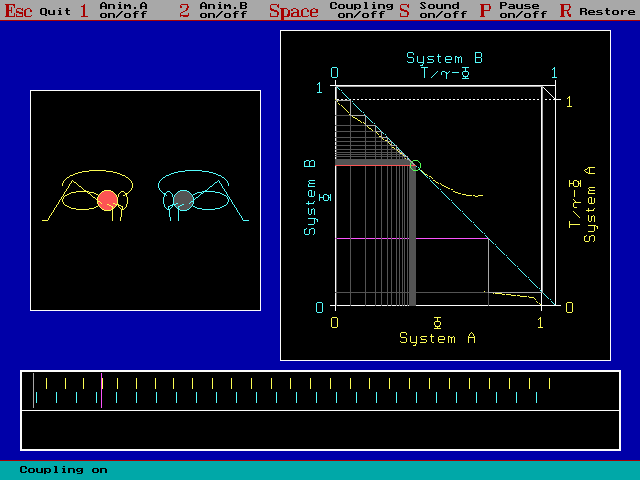
Fig. 1: Animal (yellow) phase couples to a constant singers rate ("deaf animal"; blue). Green circle marks the stable point. Display of Chorusing | Simulation + PCM

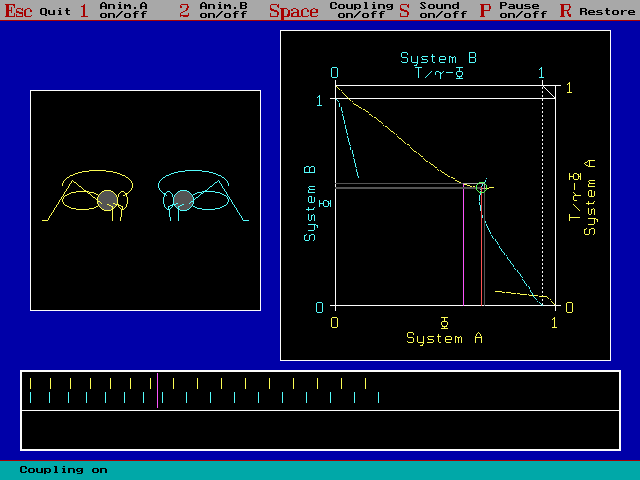
Fig. 2: Interaction of two mutually hearing animals. For these two animals there are two stable patterns of interaction. In this screen shot you can see stable alternation ... (compare with next Example)

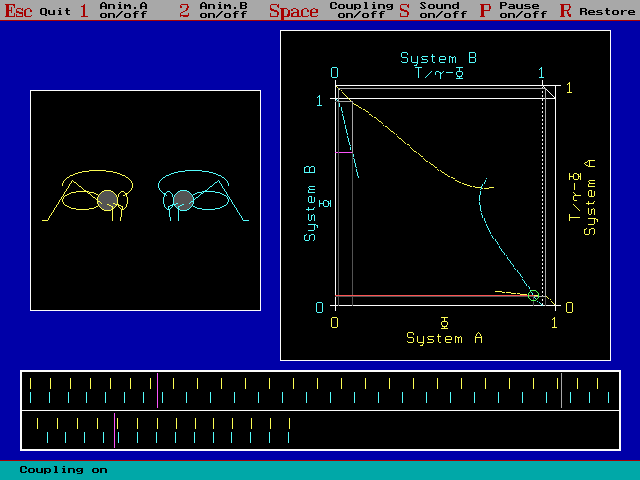
Fig. 3: ... and here imperfect synchronization. The animal with the faster freerun (blue) starts its chirps short time earlier then the endogenous slower, yellow one (compare with previous Example)

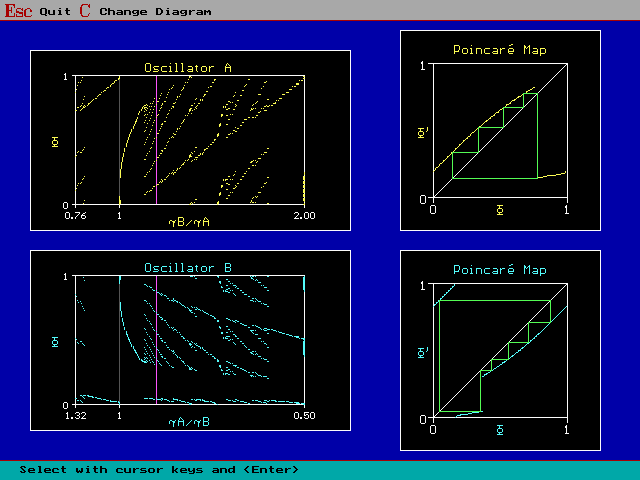
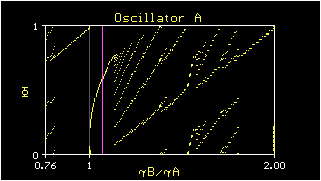
Fig. 4: Phase relationship between an animal (yellow) and constant chirp rates (stimulus) from 0.76 to 2.00 times the animals chirp rate. At the violet line (left diagrams) we find 5:6 stimulus:animal coupling; the attractor is shown by the green lines in the Poincaré maps, too (Poincaré map: phase of the others chirp in this chirp circle plotted against phase of others next chirp in the next disturbed chirp circle). Display of Bifurcation | Coupled Phases