Biological Background
First, please excuse the inferior quality of the pictures on this page. They
were hasty scanned from my thesis, and my scanner had some serious problems, too.
For this page I have taken only the most important pictures. You can see more
by following the links.
Here you find the fundamentals to understand for what I developed the programs
Kyberniidae and
Coupled Oscillators.
I don't describe the
biological "WHY" of M. elongatas calling song but the technical "HOW".
An exhaustive discussion of the biological relevance you'll find in my master thesis
"Dynamik der Gesangsinteraktion bei der Laubheuschrecke Mecopoda elongata L."
(1997; in German, sorry!) and in Sismondo (1991), or more general about calling songs
of various animals in e.g. Greenfield (1996).
Solo singers
- Adult males of Mecopoda elongata L. (Tettigoniidae, Orthoptera) are producing
nocturnal calling songs (for what ever).
- Individual males calling song consists of rhythmically repeated units, called
chirps.
- Chirps are lasting about 250 ms and are built of 10-14 pulses of increasing
intensities. Each pulse is produced by a wing stroke (katydids stridulate with their
wings).
- At an environmental temperature of 28°C the periode between two consecutive chirps
is about 1700-2000 ms. Individual differences of these freerun cycle length were observed.
Variability between consecutive chirp cycles is - at least for biological systems -
extremely small (coefficient of variation < 1%)
- Males are beginning spontanous with chirping and maintain their calling song
for about 10 minutes (sometime for 20 min and longer). Usually males restart calling
song at least 10 times during night (see
Figure, 122 kb).
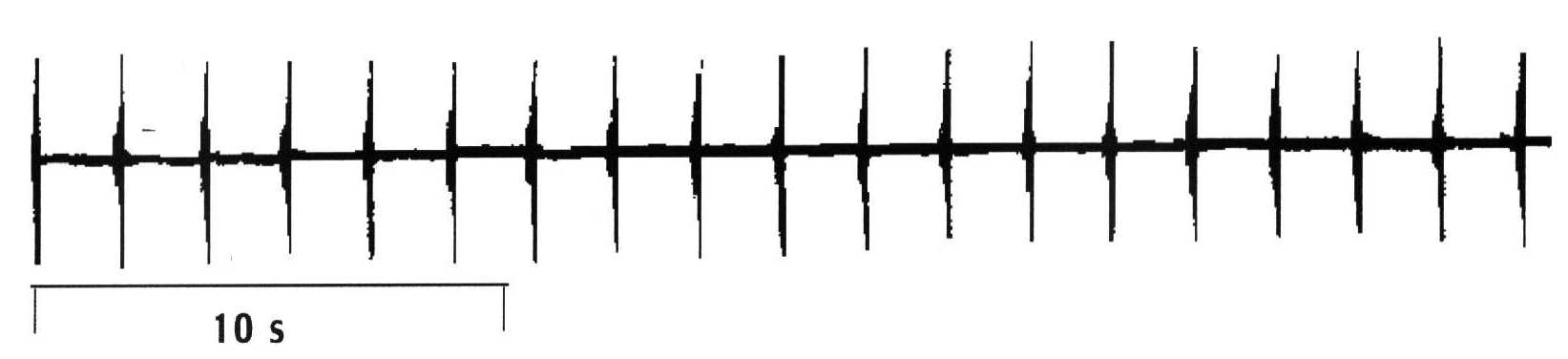
Calling song of an individual male of M. elongata.
The animal produced a chirp every 1.8 s.
Boy groups in concert
- Choirs (see Figure Oscillograms of Choirs,
but be warned: 470 kb of bad quality!) of singing males usually have very regular temporal patterns. In
laboratory with at least
30, perhaps 50 or more, singers three patterns could be discriminated even by human ear:
- distinct peaks of loudness, repeated approximately at the rate of individuals freerun,
between peaks it's silent
- distinct peaks of loudness, repeated about twice as fast as single animal repeats
its chirps; between peaks it's silent
- no distinct peaks, no distinct silent periods; noisy and "chaotic";
no rhythmic pattern to recognice.
- On pairs of singing males we found two kinds of interaction:
- imperfect synchrony, where one animal (the "leader") allmost starts its chirps 10-150 ms
before the other (the "follower").
- alternation, where the others chirps occurs approximately
on half way between the ones chirps.
Karaoke! Singing to given rhythms
- To rhythmic playback chirps (stimulus) of different rates the animals responses were
(see Figure, 170 kb):
- if stimulus periode is moderately shorter than animals chirp periode in freerun:
animals adapt their rhythm (become faster), and produce their chirps with short delay after the
stimulus chirps (imperfect synchronization), animals are consistent followers;
1:1-stimulus:animal coupling
- if stimulus periode moderately longer than animals chirp periode in freerun:
animals adapt their rhythm (become slower), and produce their chirps approximately
on half way between stimulus chirps (alternation); 1:1-stimulus:animal coupling
- if stimulus periode is too different from animals freerun (too long as like as
too short): animal can't go the stimulus rhythm; n:m-stimulus:animal-coupling
occurs
Phase Response: Influence of single chirps on individuals calling songs
- In playback experiments single chirps (stimuli) were applied to isolated singing males.
According to phase and intensity of stimuli the length of disturbed chirp circles were recorded.
- Definitions:
- I used the end of every chirp as reference for its time of occurence, the chirp ends
are loudest and therefore best to measure
- A chirp circle is the normalized periode beween a chirps end (phase
f=0) and the end of the next chirp (phase
f=1)
- A disturbed chirp circle is a chirp circle where a stimulus chirp was delivered
- An endogenous chirp circle (= a chirp circle in freerun) is given
when no stimulus was delivered for at least 5 circles
- Methode:
- Animal began singing spontanously.
- A conspecific stimulus chirp was given in every fifth chirp circle at random phase
(see figure Stimulation, 70 kB).
- Disturbed circle lengths (and lengths of the following circles, too) were plotted against
stimulus' phase in chirp circle (Phase Response Curve, see figure below)
- Results:
- Stimuli of sufficient intensity (at least 48 - 58 dB SPL) caused at most phases an alteration
of the disturbed circle length (see figure below; in figure all PRCs, 170 kb,
you can see the results of 10 animals).
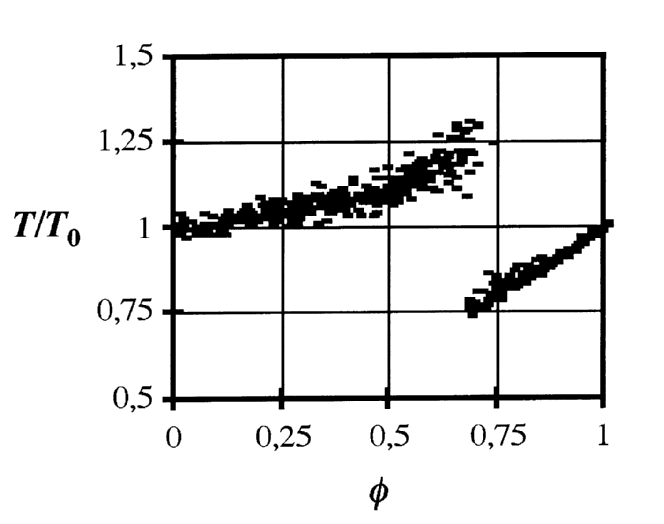
- Until the discontinuity at phases f=0.55 to 0.75
the disturbed circle lengths T
increase from 1 time to maximal 1.45 times the endogenous circle length
T0.
- From discontinuity to phase f=1 (the next chirp)
the disturbed circle lengths T
increase from minimal 0.55 times to 1 time the endogenous circle length
T0.
- The phases of discontinuities depend on stimulus' intensity. Their
phases increase with increasing stimulus' intensities (we assume that this is
caused by the "triangular" shape of chirps - their increasing loudness).
- The disturbed circles following circles were not or negligible altered (see figure
PR+1C), 79 kb).
|
Typical phase response to stimulus chirps of high intensity (78 dB SPL).
Abscissa: normalized phase of stimulus (f) in chirp circle.
Ordinate: Deviation from undisturbed circle length;
T: length of disturbed circle,
T0: circle length in freerun.
|
The model
- Based on the experimental results I developed a noise-free model to predict the interaction
between two singing animals (for a similar model see Soucek, 197?).
What do we need to know for the model:
- Individual freerun circle lengths (Condition: Maintainance of a constant
endogenous rhythm)
- Individual phase response curves (Condition: Circles following the disturbed
ones must not be altered)
- Nothing else
- Graphical coupling of two oscillators - the recipe (compare with figure below):
- Draw PRC of first animal (A), but subtract
phase f from PRCs y-value for new y-axis (B)
- Do the same with PRC of second animal, but adapt diagrams size to the ratio
between the freerun circle lengths of both animals. Then mirror the diagram horizontally and
rotate it 90° clockwise (C)
- Put one PRC upon the other as you see in (D)
- How should this work? See Kyberniidae!
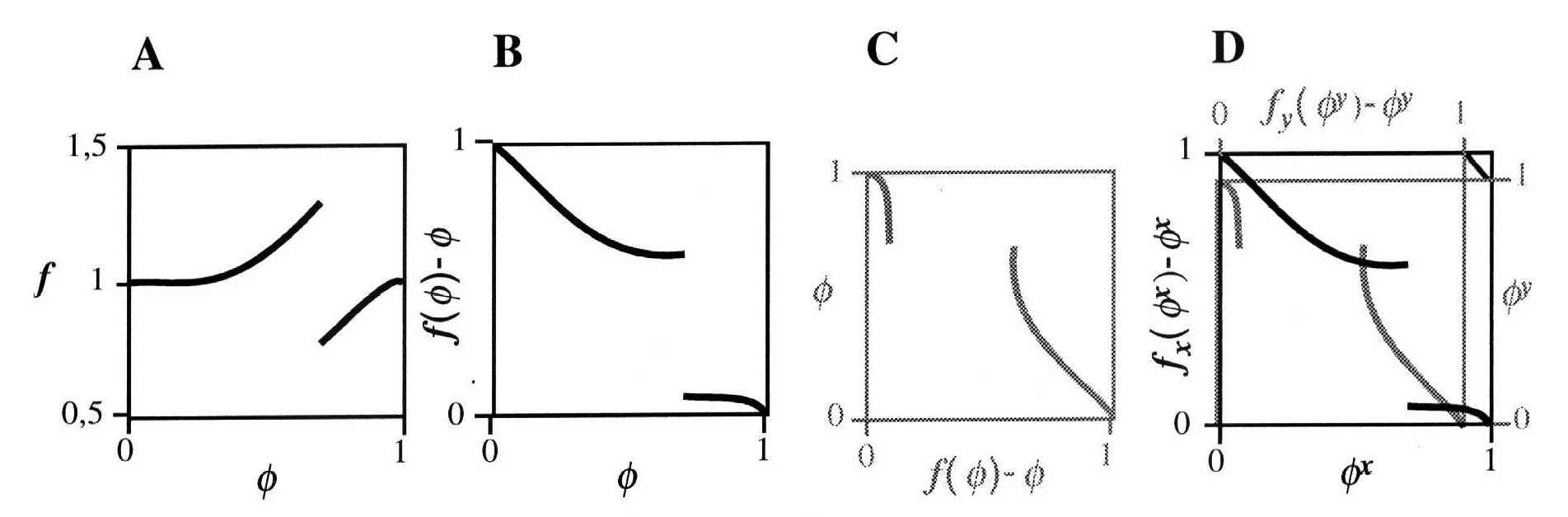
Graphical coupling of two oscillators. See text.
Does reality match the model?
- It seems that real life works!
- You can repeat the situation of the figure below. Tier #X in
Kyberniidae "is"
the animal of this record. Let it interact with periodic stimuli of 2100, 2950 and 3050 ms
cycle length and you'll get the described patterns.
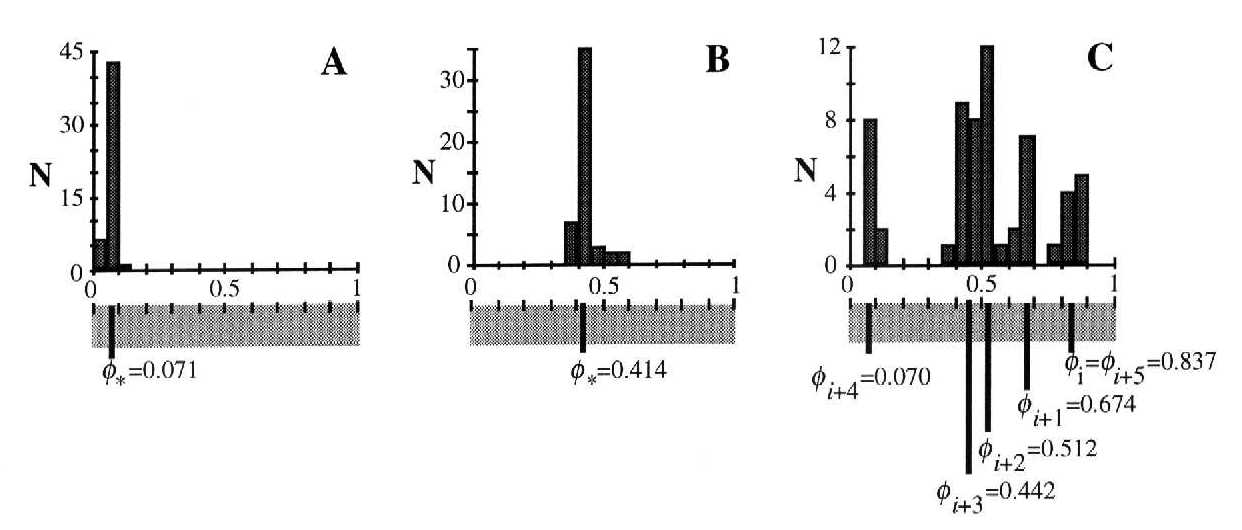
Reality versus model. Phase histograms of a males chirps in constant stimulus' cycles
(figure of recording, 170 kb).
Below you see the predicted phases. Individuals freerun cycle length was 2450 ms
(these experiment were done at 22°C, therefore the slower rhythm); stimulus cycle
were 2100 (A ), 2950 (B) and 3050 ms (C).
Cellular Automata
- Choirs of hundreds or thousands "singing animals" I modeled as cellular automata
(Coupled Oscillators)
- Every cell is is an oscillator specified by the parameters described in the
Model -
through phase response curve (PRC) and cycle length in freerun.
- Additional PRC as well as cycle length can be gaussian noisy.
- In the first place I did this work for fun and it wasn't part of my masterthesis.
Thus I have no empirical data, whether the resulting patterns are comparable with real choirs.
(I'm afraid the experimental verification could pose some problems, too)
- At least nice patterns can be observed: helices, rings, waves, ...