Zurück zur Start Seite

Entwicklung eines 2 mal doppelt wirkenden selbstanlaufenden Stirlingmotors vom a-Typ zur
Nutzung von Nieder- bis Mitteltemperatur Wärmequellen.

Dipl.-Ing. Peter Fette
Am Schäferloch 16, 75045 Walzbachtal / Germany

Inhaltsverzeichnis

• Zusammenfassung

• Arbeitsweise der neuen Maschine

• Entwicklungspotential des Stirling Prozesses

• Wämeübergang

• Die Abdichtung der Maschine

• Die Regelung der Maschine

• Der thermische Wirkungsgrad h_therm

• Ausnutzungsgrad "n" und   "e _i"

• Der zyklische Drehmomentverlauf

• T-S Diagramme der Arbeitsprozesse

• Anwendung als Kühlmaschine

• Fazit

• Tabelle 1

• Literatur Verzeichnis

Zusammenfassung

Sonnenenergie weltweit so zu erschliessen, dass sie uns elektrische und mechanische Energie liefert, und Sonnenenergie speicher- und transportfähig zu machen, sind die grössten Herausforderungen unserer Zeit. Das gilt nicht nur für Wissenschaft und Technik, sondern gleichermassen für Wirtschafts- und Umweltpolitik. Die Wasserstoff- Energiewirtschaft |1|, |2| und der Stirling-Motor sind realisierbare Antworten auf diese Herausforderung.

Der hier vorzustellende Stirlingmotor ist einfach und billig herzustellen, er eignet sich zum Einsatz in kleinen und grösseren Kraftwerken zur Stromerzeugung und damit zur Wasserstoffgewinnung. Er kann auch zum direkten Antrieb von Pumpen, oder als Schiffsantrieb eingesetzt werden.

In solarthermischen Kraftwerken ist der Stirlingmotor aufgrund seines Arbeitsprinzips wohl die einzige thermische Kraftmaschine, die kostengünstiger und -bei den relativ niederen Temperaturen- mit besserem Wirkungsgrad als Dampfmaschinen eingesetzt werden kann. Der hier vorzustellende Stirlingmotor wurde speziell zur Nutzung von Nieder- und Mitteltemperaturwärme als eine 2 mal doppelt wirkende Maschine für niedere Drehzahlen konzipiert. Zwar erreichen Hochtemperatur Stirlingmotoren auch höhere Wirkungsgrade, brauchen dafür aber in solarthermischen Kraftwerken teure dem Sonnenstand in 2 Achsen nachgeführte Hohlspiegelsysteme. Der hier beschriebene Motor arbeitet in einem Temperaturbereich der Wärmequelle von ca. 100 bis 300 Grad C und kommt darum mit einfachen erheblich preiswerteren Sonnenkollektoren aus; oder ggf. mit Parabolrinnen Kollektoren, die in |5| und |6| beschrieben sind. (Parabolrinnenspiegel werden nur in 1 Achse dem Sonnenstand nachgeführt)
Ein weiterer Vorteil der neuen Maschine ist die einfache Möglichkeit auf andere Energiequellen umzuschalten; denn Niedertemperaturwärmeenergie kann auch aus der Verbrennung von Deponiegas oder Biogas gewonnen werden, sowie aus der Verbrennung von festen und flüssigen Brennstoffen.

Eine Besonderheit dieser Maschine ist die Wärmeübertragung auf bzw. die Kühlung des Arbeitsfluids. Die Wärmequelle bzw. der Erhitzer sowie der Kühler können extern von der Maschine stehen; denn eine Flüssigkeit in Erhitzer bzw Kühler gelangt über Rohrleitungen in die Maschine, wo sie zur Energieübertragung auf das Arbeitsfluid eingesprüht wird. Bei dieser Art der Energieübertragung wird eine sehr geringe Grädigkeit erreicht.
Die Abdichtungsprobleme sind reduziert; nicht das Arbeitsgas in der Maschine, sondern eine Flüssigkeit ist gegen die Atmosphäre abzudichten. Ein weiteres besonderes Merkmal dieses neuen Stirling-Motors ist seine einfache und schnell wirkende Regelung.

Ein erster Prototyp dieser Maschine ist gebaut worden.

Die Maschine lässt sich auch als Kühlmaschine zur Raumklimatisierung einsetzen.

Nachteil der Maschine ist ihre langsame Drehzahl; darin kann diese Maschine mit grossen Schiffsdieselmotoren verglichen werden. Das muss jedoch nicht unbedingt ein Nachteil sein; denn die Energieübertragung ist auch eine Funktion der Zeit; und somit von geringere Grädigkeit, wenn mehr Zeit dafür zur Verfügung steht. Dies ist besonders im Nieder- bis Mitteltemperaturbereich von Nutzen.

Arbeitsprinzip, Konstruktionsmerkmale sowie einige grundlegende Gleichungen zur Berechnung dieser neuen Stirlingmaschine und diverse Diagramme zur Veranschaulichung der Rechenergebnisse werden in diesem Bericht dargelegt. Weitere Veröffentlichungen zu dieser Maschine siehe in |9|, |10|, |11|. Alle Berechnungen und Abbildungen sind mit dem Computerprogramm STMOT2: gemacht worden.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Arbeitsweise der neuen Maschine

In a -Typ Stirlingmotoren wird das Arbeitsfluid periodisch zwischen einem heissen Expansionszylinder und einem kalten Kompressionszylinder hin und her bewegt. In einer idealen Stirlingmaschine erfolgt diese Bewegung diskontinuierlich. Ihr Arbeitsprozess -siehe Abb. 2(P-V Diagramm) und Abb. 4a(T-S Diagramm) - entspricht 4 Zustandsänderungen, die in der idealen Maschine nacheinander erfolgen: isotherme Kompression von (I) bis (II); isochore Wämezufuhr von (II) bis (III); isotherme Expansion von (III) bis (IV); und isochore Wämeabfuhr von (IV) bis (I); siehe |3| und |4|. Längs der isochoren Zustandsänderungen bei V_max und bei V_min wird keine Ausdehnungsarbeit verrichtet; jedoch muss bei V_min eine beträchtliche Energiezufuhr und bei V_max ein Wärmeentzug erfolgen. Die Energiemengen sind einander äquivalent. Sie sollen darum im Prozess bleiben. Ein Regenerator bewirkt, dass sie intern gegeneinander ausgetauscht werden können.

In einer realen Maschine (1 Zylinder-Verdränger/Kolben Maschine oder 2 Zylinder-2-Kolbenmaschine) können die isochoren Gaswechsel Vorgänge nicht diskontinuierlich zu der Kolbenbewegung erfolgen. (Die Massenkräfte wären zu gross.) Das Aufeinanderfolgen der Zustandsänderungen kann aber in einer 2 Zylinder Maschine angenähert werden, wenn sich deren Kolben zueinander versetzt bewegen. Basis für die hier vorgestellte Maschine nach Abb. 1 ist eine solche 2 Zylinder-2-Kolben Maschine mit dem Expansionszylinder "H1" und dem Kompressionszylinder "K1" . Ihre Kolben bewegen sich mittels der beiden Kurbeltriebe "Ku1" und "Ku2" um d = 90 Grad zueinander versetzt. Eine ausführliche Beschreibung der Arbeitsweise einer 2 Zylinder Stirlingmaschine, die auch a -Typ Stirlingmotor genannt wird, ist in |3| nachzulesen, oder auf der Seite: Wie arbeitet der Stirlingmotor auf dieser Homepage.
Ein einfach wirkender a -Typ Stirlingmotor kann dadurch, dass maan das Arbeitsfluid auch auf der Rückseite der 2 Kolben wirken lässt, zu einem doppelt wirkenden Motor erweitert werden. Bei der hier vorzustellenden Maschine ist es nun weiter möglich, 2 solche doppelt wirkenden Motoren zu einer 4 -fach wirkenden Maschine zu zusammenzuschalten, die dann sogar vonselbst starten kann. Eine detaillierte Beschreibung, wie aus einem 1-fach wirkenden a -Typ Stirlingmotor diese 4-fach wirkendee a-Maschine entstanden ist, finden Sie auf dieser Homepage auf der Seite: Die Entstehungsgeschichte dieser Maschine .

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Entwicklungspotential des Stirling Prozesses

Ein wichtiges Entwicklungspotential des Stirlingmotors liegt in der Wärmeübertragung auf das Arbeitsgas. Bei Wärmezufuhr während der Expansion und bei Wärmeabfuhr während der Kompression sollte die Wärmeübertragungsfläche in den Zylindern stets in unmittelbarem Kontakt mit dem Gas sein; sie sollte im Expansionszylinder mit dem Gasraum wachsen und sich im Gasraum des Kompressionszylinders stetig erneuern.

Dies kann nicht mehr allein durch feste Wände, sondern nur durch bewegliche bzw. wachsende Wärmeaustauschflächen erreicht werden. Durch diese Option der Wärmeübertragung in den Zylindern kann das "schädliche" Volumen -oder auch Totvolumen genannt- erheblich reduziert werden, sodass es im wesentlichen nur noch aus dem Regeneratorvolumen besteht. Das Kompressionsverhältnis V_max/V_min kann deutlich erhöht werden.

Eine weitere wahlweise wünschenswerte Option ist, die Maschine mit "compound fluid" einem aus Gas + Dampf zusammengesetzten Arbeitsfluid zu betreiben. Dies ist bereits von G. Walker |7| beschrieben worden, konnte aber bisher nicht realisiert werden. Hier soll der Dampdpartialdruck einer im heissen Expansionszylinder verdampfenden Flüssigkeit zur zusätzlichen Drucksteigerung beitragen. Daraus resultiert dann mehr Nutzarbeit pro Umdrehung. Ein Nachteil dieses "compound fluid" ist jedoch eine Verringerung des thermischen Wirkungsgrades, hervorgerufen durch die Kondensation des Dampfes in den kalten Zonen der Maschine, wobei die Kondensationsenergie dem Arbeitsprozess verloren geht. Näheres dazu wird im Kapitel Der thermische Wirkungsgrad beschrieben.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Der Wärmeübergang

Die Maschine - Abb. 1 - besteht aus 8 Zylindern, die, paarweise in U-Rohranordnung verbunden, auf 2 Kurbeltriebe wirken. Eine detaillierte Beschreibung, wie diese a -Typ Maschine entstanden ist, finden Siee auf der Seite: Die Entstehungsgeschichte dieser Maschine auf dieser Homepage.
Im geradlinigen Teil jedes der 4 U-Rohre befindet sich ein Kraft übertragender Kolben, der zu beiden Seiten von einer Arbeitsflüssigkeit umgeben ist, die bis in die Zylinder reicht. Diese Flüssigkeit ist beheizt, bzw. gekühlt, wobei die eigentlichen Wärmeübertrager für die Beheizung und Kühlung ausserhalb der Maschine liegen. Über der Flüssigkeit befindet sich ein unter Druck stehendes Gaspolster, das Arbeitsgas. Mittels der Flüssigkeit wird nun dieses Gas in den jeweiligen Zylindern beheizt bzw. gekühlt. 2 Varianten für die Energieübertragung sollen hier vorgestellt werden:

1. Beregnung des Gases mit der Arbeitsflüssigkeit über Einspritzdüsen im Kopfteil jedes Zylinders. Diese Art der Wärmeübertragung auf ein Gas ist dem Wettergeschehen in unserer Atmosphäre nachempfunden. Je Zylinder ist hier eine Pumpe nötig, die die Flüssigkeit aus dem unteren Teil des Zylinders ansaugt, sie über externe Wärmeübertrager -z.B. Sonnenkollektoren bzw. Kühler- leitet, und sie dann den Einspritzdüsen zuführt.

2. Wärmeübertragungseinbauten zur Beheizung und Kühlung des Arbeitsgases im Gasraum jedes Zylinders. Die Flüssigkeit vor und hinter dem Kolben wird mit der Kolbenbewegung zunächst durch Wärmeübertrager gedrückt und benetzt dann im Gasraum diese Einbauten, die z.B. spiralförmig aufgewickelte Maschendrahtnetze oder Metallspäne sein können. Die Wärmeübertrager sowie die Mantelflächen der Zylinder werden von einer -nicht durch den Gasdruck im Zylinder beeinflussten- 2. Flüssigkeit durchströmt, die in externen Wärmeübertragern beheizt bzw. gekühlt wird.

In beiden Varianten für die Wärmeübertragung, die z.T. auch miteinander kombiniert werden können, steht dem Gas direkt im Arbeitszylinder eine grosse Wärmeübertragungsfläche zur Verfügung, die mit der Expansion wächst, und die sich bei der Kompression, wenn das Gas beregnet wird, stetig erneuert, sodass hier Wärmeübergänge mit geringer Grädigkeit erreicht werden. Wählt man eine Arbeitsflüssigkeit, deren Dampfdruck in dem infrage kommenden Temperaturbereich hoch genug ist, dann kann man eine u.U. beträchtliche zusätzliche Drucksteigerung im Expansionszylinder erreichen. Es wird dabei jedoch ein Flüssigkeitstransport aufgrund von Verdampfung und Kondensation eines Teils der Arbeitsflüssigkeit aus dem Expansionszylinder in den Kompressionszylinder hinein erfolgen, der durch geeignete konstruktive Massnahmen rückgängig gemacht werden muss. Die Verdampfung der Arbeitsflüssigkeit hat noch einen weiteren Vorteil: Durch die schnelle Bewegung der Dampfmoleküle wird eine gute Durchmischung von Dampf und Gas erreicht, was den Wärmeübergang an das Gas weiter verbessert und die Grädigkeit noch weiter herabsetzt. Wie jedoch oben schon angedeutet, werden wir im Kapitel Der thermische Wirkungsgrad h_therm auch auf die damit verbundene Verringerung des Wirkungsgrades zu sprechen kommen.

Der Übersicht halber sind in Abb. 1 die Einrichtungen für die Wärmeübertragung nicht miteingezeichnet; siehe dafür die Skizze in Abb. 6 . Aus Abb.1 soll lediglich die Arbeitsweise dieser 2 x doppelt wirkenden Stirlingmaschine ersichtlich sein.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Die Abdichtung der Maschine

Die Abdichtung des Arbeitsgases an Kolben und Kolbenstangen ist in herkömmlichen Maschinen oft ein Problem. Bei dieser Maschine ist die Abdichtung einfacher. Nur 4 Kolbenstangendichtungen gegen die Atmosphäre sind hier nötig; und diese sind keine komplizierten Gas Dichtungen sondern Dichtungen gegen druckbeaufschlagte Flüssigkeit, wie sie in der Hydraulik bekannt sind. Ebensolche aus der Hydraulik bekannten Dichtungen werden für die 4 Kolben benötigt.

Soll die Maschine nur zur el. Stromerzeugung eingesetzt werden, dann ist auch eine hermetisch dichte Konstruktion möglich. Siehe dazu die Beschreibung der Patentschrift DE 38 15 606. Es werden dann die mechanischen Kurbeltriebe durch eine Kombination von el. Lineargenerator und Linearmotor ersetzt, die anstelle der Kolben in den kalten Zylindern der Maschine sitzen. Die Kolbenstangen der heissen Kolben, werden geradlinig verlängert bis zu dieser Generator/Motor Kombination. Eine elektronisch gesteuerte Phasenversatzregelung hält den 90 Grad Phasenversatzwinkel aufrecht. Die Kompressionsarbeit wird dann durch den Motorteil verrichtet, während in den Expansionsphasen der Lineargenerator el. Energie liefert.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Die Regelung der Maschine

Die Regelung von herkömmlichen Stirlingmaschinen geschieht z.B. durch Veränderung der Gasladung durch Druckabsenkung / Druckerhöhung mittels eines Gasreservoirs und eines Kompressors. Viel einfacher lässt sich bei der hier vorgestellten Maschine eine Lastregelung realisieren:

1. In dem das sogen. "schädliche Volumen" verändert wird. Dadurch soll die Gasmasse, die in dem Prozess jeweils zwischen dem heissen und kalten Zustand hin- und herbewegt wird, verringert oder erhöht werden. Die Flüssigkeit jeweils links und rechts vom Arbeitskolben wird zur Leistungsverringerung zu einem Teil in die Regelzylinder RC gezogen; siehe Abb. 6 hier die Regelzylinder RC3 und RC4. In Abb. 1 sind die Regelzylinder unterhalb der Zylinder K3-K4 angedeutet. Es verbleibt dann ein entsprechend grosser Teil des Gases auch in der oberen Totpunktlage des Kolbens immer in dem jeweiligen Arbeitszylinder und nimmt nicht mehr am Energieaustausch teil, gleichzeitig sinkt der Gasdruck. Zur Leistungssteigerung kann die Flüssigkeit aus den Regelzylindern wieder in das U-Rohr gedrückt werden. Ein Regelungsvolumen von je 25% des Kolbenhubvolumens ergibt die kleinere Teillastkurve in dem P-V Diagram der Abb. 2 und in dem T-S Diagramm der Abb. 4a.

2. Über die Energiezufuhr lässt sich auch eine schnelle Regelung erzielen, wenn die Wämeübertragung auf das Arbeitsgas durch Beregnung mit heisser Arbeitsflüssigkeit erfolgt; hier kann der Beregnungsstrom gedrosselt bzw. verstärkt werden.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Der thermische Wirkungsgrad h_therm

Der thermische Wirkungsgrad h_therm ist bei isothermem Wärmeübergang (die Temperaturen TE in den Expansions- und TC in den Kompressionszylindern sind konstant) und bei 100% Wärmeaustausch im Regenerator gleich dem Carnot-Wirkungsgrad

h_therm = (TE - TC)/TE.

Dieser ideale thermische Wirkungsgrad wird natürlich in der realen Maschine nicht erreicht. Der Wärmeübergang ist zwar gut, aber eben nicht isotherm. Eine Grädigkeit lässt sich aus den Wärmekapazitäten der Beregnungsflüssigkeitstropfen (bzw. aus den der Metallspäne) und der Wärmekapazität des Gases errechnen. Sie ist experimentell bestätigt worden. Bei der Wärmeübertragung auf das Gas spielen die Grösse und die Masse der Wärmeaustauschfläche, die Gasgeschwindigkeit an dieser Fläche, die Wärmeleitfähigkeit des Gases, sowie die Güte des Regenerators eine Rolle. Reibungsverluste in der Gas- und Flüssigkeitsströmung, sowie Verluste im Regenerator verringern den Wirkungsgrad. Ähnlich wie bei Schiffsdieselmotoren kann auch bei diesem Stirlingmotor durch grossvolumige Bauweise eine höhere Leistung erzielt werden. Berechnungsgrundlagen siehe |11|.

Wird "compound fluid" also Gas + Dampf (z.B. Wasserdampf) als Arbeitsfluid genommen, dann führt der Wasserdampf Partialdruck zu einer zusätzlichen Drucksteigerung in der Maschine. Dieses wiederum resultiert in mehr Nutzarbeit pro Umdrehung in der Maschine. Die Dampfentstehung hat wie schon oben erwähnt einen weiteren Vorteil: Infolge der schnellen Bewegung der Dampfmoleküle durch das Gas erfolgt auf die Gasmoleküle ein noch besserer Wärmeübergang als dieser ohnehin schon dadurch erzielt wird, dass die eingesprühte Flüssigkeit eine grosse Wärmeübertragungsfläche mit sich bringt.
Dennoch hat "compound fluid" einen Nachteil, der nur dann nicht so sehr ins Gewicht fällt, wenn die Wärmeenergie praktisch kostenlos zur Verfügung steht, wie bei der Solarenergie, sodass "nur" höhere Kosten wegen mehr Kollektorfläche anfallen. Der Grund ist folgender:
Der Dampf, der im Expansionszylinder entsteht, wird in der Regeneratorleitung und im kalten Kompressionszylinder kondensiert. Die Kondensationsenergie wird -hauptsächlich im Kompressionszylinder- weggekühlt und geht dem Prozess verloren. Die entstandene Flüssigkeitsmenge muss dem Expansionszylinder wieder zugeführt werden. Die Aufheizung dieser zurückgeführten Flüssigkeitsmenge auf die Temperatur im Expansionszylinder TE und die Verdampfungsenergie bei TE während der Expansion muss für jede Umdrehung erneut eingebracht werden. Vergleicht man die "Rahmen" in Abb. 4a und in Abb. 4c, dann wird diese Wirkungsgradeinbusse deutlich:

• Abb. 4a -idealer Stirlingprozess nur Gas als Arbeitsfluid- hier ist die Masse des Gases immer konstant. Bei idealem Regenerator hat dieser Prozess den Carnot Wirkungsgrad; denn durch den Wärmeaustausch im idealem Regenerator wird die isochore Wärmezufuhr bei V_max und der Wärmeentzug bei V_max realisiert.

• In Abb. 4c bildet der "Rahmen" den idealen theoretischen Prozess, wenn Dampf allein das Arbeitsfluid ist. Man erkennt, dass dieser "Rahmen" nicht einmal angenähert ein Parallelogramm bildet. Dies wäre jedoch die Vorausetzung für den 100 % isochoren Wärmeaustausch über den Regenerator, um den Carnot Wirkungsgrad zu bekommen. Bei V_max kondensiert im idealen Dampf-Stirling Prozess die grösste Masse des Dampfes bis zum Gleichgewicht mit der im Kompressionszylinder herrschenden Temperatur TC. Nur ein kleiner Rest Dampf ist noch bei dieser Temperatur TC vorhanden und wird im nächsten Schritt des Prozesses bis V_min komprimiert.
  Die in den Expansionszylinder zurückgeführte Kondensatmenge muss auf die Temperatur TE aufgeheizt werden, und während der Expansion muss neuer Dampf erzeugt werden. Die Energie dafür wird nur im Expansionszylinder aufgebracht.
  Bestenfalls könnte der Regenerator die geringe Dampfmasse, die bei V_max noch übrig ist, auf TE aufheizen, da nur diese Dampfmasse durch den Regenerator geleitet wird.

Halten wir fest: Die Kondensatenergie geht dem Stirlingprozess mit Dampf als Arbeitsfluid verloren, dadurch wird der thermische Wirkungsgrad deutlich kleiner als der Carnot Wirkungsgrad. Dennoch kann es sich lohnen, einen Stirlingmotor mit "compound fluid", einem aus Gas + Dampf zusammengesetzten Arbeitsfluid zu betreiben, da die verrichtete Nutzarbeit pro Umdrehung mit diesem Arbeitsfluid deutlich zunimmt. Weiteres wird im Kapitel T-S Diagramme der Arbeitsprozesse erläutert.

Das Computerprogramm STMOT2: basiert auf den Berechnungsgrundlagen in |11| und berücksichtigt alle diese Verluste.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Ausnutzungsgrad "n" und   "e _i"

Neben dem thermischen Wirkungsgrad ist der Ausnutzungsgrad "n" eine interessante Kenngrösse. "n" ist das Verhältnis der Nutzarbeit der realen Maschine "W" zu der Nutzarbeit des idealen Stirlingprozesses "W _i " (kein Totvolumen, Regeneratorvolumen = 0) im gleichen Arbeitsraum zwischen V_max und V_min

Für das Zylinderpaar H1-K1 bei isothermem Wärmeübergang entspricht der Nutzarbeit "W" die durch die Kurve in Abb. 2 oder in Abb. 4a eingeschlossenen Fläche.
Der Nutzarbeit des idealen Stirlingprozesses "W _i " entspricht die Fläche in Abb.2 oder die Fläche des "Rahmens" in Abb.4a , die durch die Isothermen TE und TC sowie durch die Isochoren bei V_max und V_min gebildet wird). Fläche (I) - (II) - (III) - (IV) - (I):

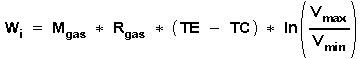
oder

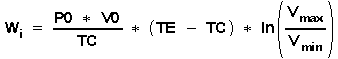
P0, V0, T0 sind Druck, Volumen und Temperatur des Gases in der Ruhestellung der Maschine. Die Temperaturen TE im Expansions- und TC im Kompressionszylindern sind konstant.

Die Nutzarbeit "W _i" des idealen Stirlingprozesses ist nach obiger Gleichung bestimmt durch die Temperaturen TE und TC sowie durch das erreichbare Volumenverhältnis V_max/V_min und ist direkt proportional der Gasmasse M_gas in den Zylindern, und damit auch bestimmt durch das Ruhevolumen V0 und den Ruhedruck P0. Grundsätzlich gilt dies auch für die Nutzarbeit "W" in der realen Maschine. Das Volumenverhältnis V_max / V_min wird durch Regelungsvolumen, Regeneratorvolumen "VR", den Versatzwinkel d, durch sonstige Totvolumina in der Maschine und durch die geometrischen Verhältnisse der Kurbeltriebbewegung, die ja den idealen Bewegungsablauf nur annähern kann, bestimmt.
V_max/V_min und damit "W" und der Ausnutzungsgrad "n" werden geringer mit steigendem Totvolumen (das ist der Totraum in den Zylindern + Regeneratorvolumen + Regelvolumen). Ebenfalls verringert sich V_max/V_min, wenn statt des rein sinus-förmigen Bewegungsablaufs der Kolben durch die Kreuzschwingen Kurbeltriebe Pleuelstangen Kurbeltriebe verwendet werden, siehe |11|.

Die obige Definition des Ausnutzungsgrades "n" lässt nur eine Ausage zu über das Verhältnis der Arbeit des realen zum idealen Stirling-Prozess jeweils in den gleichen Grenzen von V_max und V_min. Mit diesem Ausnutzungsgrad können aber nicht verschiedene Maschinen miteinander verglichen werden, die jeweils unterschiedliche Volumenverhältnisse V_max/V_min haben.
Um mit dem Ausnutzungsgrad eine allgemein gültige Aussage über den Arbeitsgewinn einer Stirlingmaschine zu definieren, sollte man die Arbeit "W _i" einer idealen Referenzmaschine, die ein festes Volumenverhältnis hat, benutzen, und damit einen Ausnutzungsgrad "e _i" definieren. Diese Referenzmaschine sollte sowohl für einfach wirkende Maschinen wie auch für die einzelnen Teilmaschinen in doppelt und mehrfach wirkenden Stirlingmaschinen als Vergleichsobjekt dienen. Eine derartige ideale Referenzmaschine könnte als 2 Zylinder - 2 Kolbenmaschine folgendermassen definiert werden:

• Idealer Regenerator; aber Regenerator-Volumen VR = 0.; kein sonstiges "Totvolumen".
• Ideale sinus-förmige Kurbeltrieb Bewegung. Winkelversatz von d = 90 Grad zwischen Expansions- und Kompressionsbewegung.
• Expansionshubvolumen = Kompressionshubvolumen. Gleiche Zylinderquerschnittsfläche in beiden Zylindern: FQE = FQK = FQ.
• Aus obigen 3 Bedingungen ergibt sich, dass das Volumenverhältnis V_max/V_min jetzt unabhängig vom Hubvolumen ist. V_min ist erreicht bei j = 45 Grad und V_max bei j = 225 Grad. Dann wird:

  

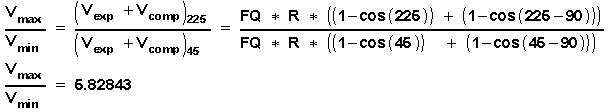
• Die obere Temperatur des Prozesses TE ist die maximale im Erhitzer auftretende Temperatur.

• Die untere Temperatur des Prozesses TC ist die minimale im Kühler auftretende Temperatur.

• M_gas ist die gemessene Gasmasse in der zu vergleichenden realen Maschine. Mit dieser Gasmasse wird der ideale Stirling Referenzprozess gerechnet. Bei zusammengesetzten Arbeitsfluiden soll mit M_gas die Masse der Arbeitsfluide (Gase) definiert werden, die während einer Umdrehung konstant bleibt und auf die mit genügender Genauigkeit die "Zustandsgleichung idealer Gase" (manchmal auch in sprachlich laxer Weise als das "ideale Gasgesetz" bezeichnet) angewendet werden kann. (Dämpfe, die in der Maschine kondensieren können, werden nicht zu M_gas gerechnet)

Mit der Gasmasse M_gas, den Temperaturen TE = T_max und TC = T_min und dem festen Volumenverhältnis
V_max/V_min = 5.82843 errechnet sich die Arbeit des idealen Stirling Referenzprozess W_ir gemäss obiger Formel für W_i zu:

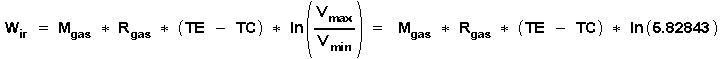
Der neue Ausnutzungsgrad e_i zur idealen Referenzmaschine wäre dann mit oben definiertem "W _ir" nunmehr von allgemeiner Gültigkeit für Vergleiche aller Stirlingmotoren.

Der Ausnutzungsgrad e_i besagt:

"Wie gut ist eine Maschine bei vorgegebener Gasladung M_gas, die über P0, V0 und T0 gemessen werden kann, und vorgegebenen Maximal- und Minimaltemperaturen TE und TC im Vergleich zu einer optimalen idealen Stirling Referenzmaschine mit der gleichen Gasladung und den gleichen Maximal- und Minimaltemperaturen."

Die Zusammenfassung der Rechenergebnisse in Tabelle 1 zeigt den Einfluss der oben erwähnten Parameter auf die Nutzarbeit "W" und auf den Ausnutzungsgrad e_i. Zusätzlich wird in dieser Tabelle die Veränderung der Ergebnisse aufgelistet, wenn anstelle der rein sinusförmigen Kolbenbewegung mittels einer Kurbelschleife ein Pleuelstangen Kurbeltrieb verwendet wird. Mit einem Pleuelstangen Kurbeltrieb bekommt man ein kleineres Volumenverhältnis
V_max/V_min als mit einer Kurbelschleife. Siehe auch |11|.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Der zyklische Drehmomentverlauf

Der zyklische Drehmomentverlauf der 8 Zylinder Maschine ist wegen der 4 Arbeitstakte pro Kurbelwellenumdrehung stets >0 und ist einer 4-fachen Sinus-Linie ähnlich; siehe die Kurve DR1234 in Abb. 5; errechnet mit dem Programm STMOT2: ; siehe auch |11|.

Werden 2 dieser Maschinen unter einem Kurbelwellenversatz von Y = 45 (135, 225, oder 315) Grad gekoppelt, dann erhält man ein nahezu konstantes Drehmoment. Die hier noch zu sehenden Schwankungen in der Kurve   DREH12 ergeben sich, weil das Kolbenstangen Volumen die Gasladung der 4 einzelnen Teilmaschinen unterschiedlich beeinflusst.
Bei gleichem Ruhedruck P0 in allen Teilmaschinen ist in der Teilmaschine "H3-K3" die meiste Gasmasse vorhanden, da hier die Kolbenstangen keinen Einfluss haben. Die Teilmaschinen "H1-K1" und "H2-K2" haben gleiche Gasmassen; hier wird das Hubvolumen in "K1" bzw. in "H2" durch die Kolbenstange beeinflusst. In der Teilmaschine "H4-K4" werden die Hubvolumina beider Zylinder von den Kolbenstangenvolumina verringert, sodass hier die kleinste Gasmasse vorliegt. Diese, wenn auch geringen Unterschiede in der Gasladung haben zur Folge, dass in den einzelnen Teilmaschinen auch unterschiedlich Nutzarbeit verrichtet wird, was wiederum bewirkt, dass die Drehmomente der 4 einzelnen Teilmaschinen nicht identisch sind.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

T-S Diagramme der Arbeitsprozesse

In Abb. 4a, 4b, 4c werden 3 T-S Diagramme präsentiert. Jedes Diagramm wurde für die Teilmaschine "H1-K1" errechnet.   Abb. 4a zeigt das T-S Diagramm für ein Gas als alleiniges Arbeitsfluid. Der "Rahmen" in   Abb. 4a -wie auch schon zuvor erwähnt- entsspricht dem idealen Stirling Prozess mit den Isothermen Temperaturen "TE" und "TC" und mit den Isochoren V_min und V_max. Das Regeneratorvolumen "VR" ist =0 in diesem idealen Prozess. Im idealen Prozess laufen die Zustandsänderungen nacheinander ab.
Die Kurve innerhalb dieses "Rahmens" entspricht dem realen Stirling Prozess mit Gas als Arbeitsfluid. Sie ist mit den gleichen Temperaturen "TE" und "TC" und für das gleiche Arbeitsvolumen zwischen V_min und V_max errechnet worden, jedoch mit einem realen Regenerator dessen Volumen VR > 0 ist, sowie mit weiteren Totvolumina in der Maschine. Die Kurve berührt den "Rahmen" bei der Isochoren V_min -das entspricht einer Kurbelwinkelposition von j = 45 Grad des 1. Kurbeltriebs "KU1"- ; dann berührt sie den "Rahmen" bei der Isochoren V_max entsprechend einer Kurbelwinkelposition von j = 225 Grad.
Die sich aus der Berechnung der realen Maschine ergebende Kurve umschliesst eine kleinere Fläche als der "Rahmen" weil

1. das Regeneratorvolumen und andere Totvolumina > 0 sind, und

2. weil die Zustandsänderungen des Arbeitsfluids des realen Stirlingprozesses nicht nacheinander erfolgen können, sondern weil sie sich hier überlappen. Nebenbei gesagt, jedoch nur von theoretischem Interesse, sollte erwähnt werden, wenn in einem realen Prozess alle Totvolumina = 0 sein könnten, würde die Kurve den "Rahmen" nicht nur bei den Isochoren V_min und V_max sondern auch bei den Isothermen "TE" -hier bei der Kurbelwinkelposition von j = 90 Grad -bezogen auf "KU1" (an dieser Position wäre das Kompressionsvolumen = 0)- und bei der Isothermen "TC" -bei der Kurbelwinkelposition von j = 0 Grad bezogen auf "KU1" (hier ist dann das Expansionsvolumen = 0) berühren.

Die Fläche, die von der Kurve umschlossen wird entspricht der Nutzarbeit des realen Prozesses "W" und die Fläche des "Rahmens" entspricht der Arbeit des idealen Prozesses "W _i". (Siehe hierzu auch das Kapitel: Ausnutzungsgrad "n" und   "e_i"). Der kleinere "Rahmen" in   Abb. 4a und die darin eingeschlossene Kurve entsprechen einem Teillastprozess.

Die Abb. 4b zeigt ein T2 - S2 Diagramm des Stirling Processes für ein "compound fluid": Wenn Wasser als Arbeitsflüssigkeit gewählt wird, und Verdampfung im Expansionszylinder einsetzt, dann wird der Gesamtdruck des Arbeitsfluids durch den Wasserdampfpartialdruck erhöht. (Siehe hierzu auch das Kapitel Der thermische Wirkungsgrad h_therm) Diese Druckerhöhung wiederum bewirkt eine Steigerung der Nutzarbeit pro Umdrehung. Betrachtet man die Kurve in   Abb. 4b, dann erkennt man, dass die hier umschlossene Fläche sogar noch grösser ist, als die Fläche des "Rahmens" in   Abb. 4a, die ja der Arbeit des idealen Stirlingprozesses "W _i " für nur Gas als Arbeitsfluid entspricht. Die "Ausreisser" in der Kurve resultieren von numerischen Rechenproblemen: Die Temperatur T2 für "compound fluid" wird durch die Differentialgleichung definiert:

   T2 = ( d_Q_gas + d_Q_vapor ) / ( d_S_gas< + d_S_vapor)

In den Bereichen, wo die Summe der Entropie Differentiale d_S_gas + d_S_vapor und die Summe der Energie Differentiale d_Q_gas + d_Q_vapor beide gegen Null gehen, entstehen diese Probleme. (Der Index vapor steht für Dampf.)

Der "Rahmen" in   Abb. 4b entspricht dem idealen Stirling Prozess für compound fluid.

  Abb. 4c zeigt ein T3 - S3 Diagramm eines Stirling Prozesses allein für die Dampfkomponente. Der Rahmen in Abb. 4c entspricht wieder dem idealen Stirling Prozess. Die Kurve innerhalb dieses Rahmens ist für den realen Prozess mit nur Dampf als Arbeitsfluid errechnet worden; auch hier mit einem Totvolumen > 0. Die Temperatur T3 ist hier die Sattdampftemperatur, die zu einem mittleren Sattdampfdruckes gehört, der sich sich aus der Errechnung des Prozesses ergibt. Hier ergeben sich keine "Ausreisser", T3 wird nicht aus einer Differentialgleichung wie T2 errechnet, sondern ist aus der Dampfdrucktabelle interpoliert worden.

  Abb. 3 zeigt 2 P-V Diagramme der realen Prozesse für Gas allein sowie für Gas+Dampf als Arbeitsfluid. Die Nutzarbeit des realen Prozesses also die Fläche in der Kurve "Pgas" entspricht der Fläche in der Kurve in   Abb. 4a und die Fläche der Kurve "P" in Abb. 3 entspricht der Fläche der Kurve -inklusive der "Ausreisser"- in   Abb. 4b.

Die thermodynamischen Gleichungen, die zur Errechnung dieser T-S und P-V Diagramme benötigt werden sind in |11| veröffentlicht. Einige dieser Gleichungen finden Sie in |3|, |7|, |8|, |9| und |10|.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Anwendung als Kühlmaschine

Die hier bisher vorgestellte Maschine des 2 mal doppelt wirkenden Stirlingmotors nach Abb. 1 besteht ja aus 4 einzelnen Stirlingmaschinen bzw. es sind 2 doppelt wirkende Maschinen. Man kann jetzt eine der doppelt wirkenden Maschinen z.B. "H1-K1 und H2-K2" als Motor nehmen, der die andere doppelt wirkende Stirlingmaschine "H3-K3 und H4-K4" antreibt, die als Kühlmaschine fungiert, wie es in der folgenden Abbildung deutlich wird.

Die Maschinen "H1-K1 und H2-K2" arbeiten wie in den vorherigen Kapiteln beschrieben als doppelt wirkender Stirlingmotor, dessen Zylinder "H1" und "H2" beheizt und dessen Zylinder "K1" und "K2" gekühlt werden. Da hier jetzt pro Umdrehung nur 2 Arbeitstakte als Motor vorkommen, muss diese Maschine mit einem Schwungrad versehen werden.
Die 2. Maschine, die jetzt als Kühlaggregat arbeiten soll, wird an den Zylindern "K3" und "K4" gekühlt, um die Kompressionsarbeit zu verringern, so wie auch die Zylinder des Motors "K1" und "K2" gekühlt werden.
Die Arbeitsflüssigkeit in den Zylindern "H3" und "H4" wird jetzt gekühlt, wenn sich das Gas in der Expansionsphase befindet. Die Arbeitsflüssigkeit kann somit zur Raumkühlung weiter verwendet werden, was hier durch den hellbauen Flüssigkeitskreislauf angedeutet ist.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Fazit

Die hier vorgestellte Maschine ist ein langsam drehender Motor nach dem Stirlingprinzip: Gut regelbar, nahezu konstantes Drehmoment, besonders für die Nutzung von Niedertemperaturwärme geeignet, geringe Abdichtungsprobleme, einfacher und billiger herzustellen als Dampfturbinen. Ein Transport der Flüssigkeit infolge Verdampfung und Kondensation in die Kompressionszylinder hinein muss durch konstruktive Massnahmen rückgängig gemacht werden, oder, falls auf Drucksteigerung infolge Teilverdampfung verzichtet werden soll, muss diese Verdampfung durch Auswahl einer geeigneten Arbeitsflüssigkeit vermieden werden.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Tabelle 1     Stirling Motorberechnung. Zusammenfassung fuer eine Teilmaschine: Zylinderpaar: H1-K1

|----------------------------------------------------------------------------------------|
| Kurbelschleife                 |    Ohne Dampf nur Gas     | Arbeitsfluid: Dampf + Gas |
|--------------------------------|------------|--------------|------------|--------------|
|                                |   Vollast  |   Teillast   |   Vollast  |   Teillast   |
|                                | Regelvolu- | alle Regelvo-| Regelvolu- | alle Regelvo-|
|                 |  Dimension   | men  = 0 % | lumina = 25% | men = 0 %  | lumina = 25% |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax           | Liter        |   2.78     |    3.5       |   2.78     |   3.5        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax / Vmin:   |   -          |   4.63     |    2.6       |   4.63     |   2.6        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax           |  Bar         |  16.2      |    7.0       |  17.7      |   8.3        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax / Pmin    |    -         |   4.7      |    2.6       |   4.0      |   2.3        |
|-----------------|--------------|------------|--------------|------------|--------------|
|mittl. Drehmoment| Newton * M   |  41.7      |   15.3       |  89.4      |  45.5        |
|-----------------|--------------|------------|--------------|------------|--------------|
|umgesetzte Arbeit| Newton * M   | 271        |  100         | 569        | 290.0        |
|-----------------|--------------|------------|--------------|------------|--------------|
| e i = W/Wir * 100 |     %        |  54.2      |              | 114.1      |              |
|========================================================================================|
|Pleuelstangen Kurbeltrieb L/R=3 |    Ohne Dampf nur Gas     | Arbeitsfluid: Dampf + Gas |
|--------------------------------|------------|--------------|------------|--------------|
|                                |   Vollast  |   Teillast   |   Vollast  |   Teillast   |
|                                | Regelvolu- | alle Regelvo-| Regelvolu- | alle Regelvo-|
|                 |  Dimension   | men  = 0 % | lumina = 25% | men = 0 %  | lumina = 25% |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax           | Liter        |   2.9      |    3.7       |   2.9      |   3.7        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax / Vmin:   |   -          |   4.0      |    2.5       |   4.0      |   2.45       |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax           |  Bar         |  13.5      |    6.5       |  14.9      |   7.8        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax / Pmin    |    -         |   4.1      |    2.5       |   3.5      |   2.15       |
|-----------------|--------------|------------|--------------|------------|--------------|
|mittl. Drehmoment| Newton * M   |  35.8      |   14.2       |  80.6      |  43.4        |
|-----------------|--------------|------------|--------------|------------|--------------|
|umgesetzte Arbeit| Newton * M   | 233.6      |  94.1        | 517        | 278          |
|-----------------|--------------|------------|--------------|------------|--------------|
| e i = W/Wir * 100 |     %        |  47.1      |              | 103.7      |              |
|----------------------------------------------------------------------------------------|

Tabelle 1    Stirling Motorberechnung. Zusammenfassung fuer eine Teilmaschine: Zylinderpaar: H1-K1

Daten fuer diese Berechnung:

• Zylinder Durchmesser DH = 10 cm, DK = 10 cm

• Versatzwinkel zwischen Expansions- und Kompressionsbewegung d = -90.0 Grad

• Kurbelradius R = 10 cm

• Kolbenstangen Durchmesser DKST = 2 cm,

• Regenerator Volumen VR = 0.15 Liter, Regenerator Wirkungsgrad = 100 %,   Kein weiterer Totraum in der Maschine

• Ruhedruck P0 = 5 Bar,

• Temperaturen im Expansionszylinder TE = 400 K, im Kompressionzylinder TC = 300 K.

• Die Berechnung erfolgt fuer eine konstante Drehzahl, alle Reibungsverluste werden vernachlässigt;
  Fuer die komplette Maschine mit ihren 4 Teilmaschinen muessen die umgesetzte Arbeit und das mittlere Drehmoment mit 4 multipliziert werden.

Die Berechnungen, die den Abbildungen in diesem Bericht zu Grunde liegen, sind mit diesen Motordaten gemacht.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Literatur Verzeichnis

• |1|   J.Bockris,E.Justi: Wasserstoff die Energie fuer alle Zeiten, Konzepte einer Sonnen-Wasserstoff-Wirtschaft, U.Pfriemer Verlag Muenchen, ISBN 3-7906-0092-X 1980.

• |2|   J.Bockris, Energy: The Solar Hydrogen Alternative , Australia & New Zealand Book Co Pty Ltd.

• |3|   R.J.Meijers: Der Philips Stirlingmotor, Motoren Technische Zeits MTZ 29 (1968)/7, DK 621.41/43 (492) Philips

• |4|   H.D. Heck: Der Stirlingmotor, Bild der Wissenschaft 11/1985, ISSN 0006-2375 Deutsche Verlagsanstalt Stuttgart

• |5|   D.Kearney,D.Jaffe: The 80 MWe SEGS units in California, Modern Power Systems, July 1988,Volume 8,Issue 7, ISSN 0260-7840

• |6|   M.Geyer, H.Klaiss: 194 WM Solarstrom mit Rinnenkollektoren, Brennstoff Wärme Kraft Bd.41 1989 Nr.6, VDI Verlag Duesseldorf

• |7|   G. Walker: Stirling Engines, Clarendon Press Oxford 1980

• |8|   P.Fette: Neuer Wärmekraftprozess fuer die Nutzung von Niedertemperatur Wärme, Brennstoff Wärme Kraft Bd.39 1987 Nr.11, VDI Verlag Duesseldorf

• |9|   P.Fette: About the Efficiency of the Regenerator in the Stirling Engine and the Function of the Volume Ratio Vmax/Vmin Proceedings of 7'th International Conference on Stirling Cycle Machines ICSC '95  ICSC-95 041 Page 271
    P.Fette: Über den Energieaustausch und die Effektivität des Regenerators in der Stirlingmaschine in bezug auf das Volumenverhältnis Vmax/Vmin und die Art des Arbeitsfluids.

• |10|   P.Fette: Pressure Computation for a Stirling Engine which work with Compound Fluids. Proceedings of 7'th International Conference on Stirling Cycle Machines ICSC '95  ICSC-95 042 Page 279

• |11|    P. Fette Grundlagen für die Berechnung des Wärmekraftprozesses und der Dynamik von a -Typ Stirlingmotoren mit dem Programm STMOT2

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 1

Abb.1:    2 mal doppelt wirkender Stirlingmotor

Es bedeuten in dieser Skizze:

KW = Kurbelwelle mit Schwungrad,   KU1= unterer Kurbeltrieb, KU2= oberer Kurbeltrieb, M = Mitnehmerkupplung
H1 : Expansionszylinder, K1 : Kompressionszylinder der 1. Teilmaschine
H2 : Expansionszylinder, K2 : Kompressionszylinder der 2. Teilmaschine
H3 : Expansionszylinder, K3 : Kompressionszylinder der 3. Teilmaschine
H4 : Expansionszylinder, K4 : Kompressionszylinder der 4. Teilmaschine
WH1 - WH4 : externe Wärmetauscher für die heissen Zylinder H1 - H4
WK1 - WK4 : externe Kühler für die kalten Zylinder K1 - K4

RC Regelungs Zylinder (hier nur für die kalten Zylinder K4 und K3 skizziert)
Detailierte Information über die Regelung finden Sie im Abschnitt Regelung.

Während des Betriebes sind die 2 Kurbeltriebe "KU1" und " KU2" über die Kupplung "M" fest miteinander verbunden. Nur im Ruhezustand oder zum Flüssigkeit- und Gaseinfüllen sind die beiden Kurbeltriebe entkoppelt dabei haben beide die Winkelposition von j = -90 Grad (bezogen auf die Position von "KU1" oben in der Skizze.) Alle Kolben befinden sich dann in der Mitte des horizontalen Zylinders jeder U-Rohr Anordnung.
Der Start der Maschine aus dieser Ruheposition erfordert die Spannung der Kupplung "M" , um den 90 Grad Phasenversatz einzustellen.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 2

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 4a

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 4b

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 4c

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 5

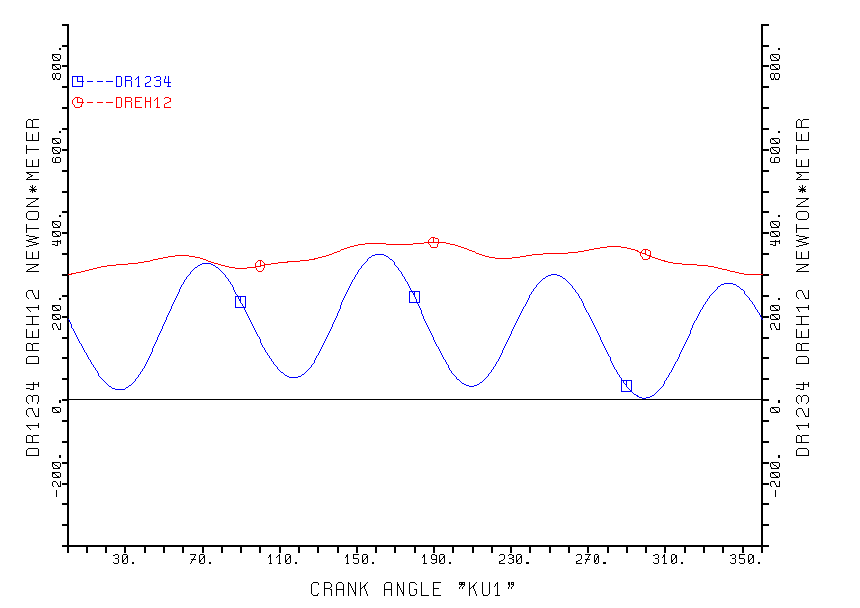
Abb.5   "DR1234" Dremomentverlauf des 2 mal doppeltwirkenden Stirlingmotors.
        "DREH12"= ist das Drehmoment von 2 unter einem Kurbelinkelversatz von Y = 135 Grad zusammengekoppelten Maschinen.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Abb. 6

Abb. 6

  2. Methode des Energietransportes an das Arbeitsfluid durch Beheizung oder -wie hier in den Kompressionszylindern- durch Kühlung der Arbeitsflüssigkeit durch einen separaten Wärmetauscher. RC3 und RC4 sind die Regelungs - Zylinder.

Um zu Ihrer vorherigen Textstelle zurück zu kommen benutzen Sie die Zurück/back Taste Ihres Browsers.

  Zurück zum Inhaltsverzeichnis

Fragen ?  

  Zurück zur Start Seite